Álxebra lineal
|
A álxebra lineal ou álxebra linear é o estudo das propiedades matemáticas xeradas polos sistemas de ecuacións lineares. Estreitamente ligados están os vectores e os espazos vectoriais, que son a base da linguaxe xeométrica usada nesta rama das matemáticas[1].
No campo de estudo da álxebra linear áchanse, entre outros, as aplicacións lineares; as matrices e os determinantes; os espazos afíns e euclidianos; as formas cuadráticas; os autovalores e os autovectores; os lugares xeométricos no plano, como as cónicas, e no espazo, como as cuádricas; as curvas no plano e no espazo; as superficies no espazo; e os tensores.
Moitos destes conceptos, son tamén obxecto de estudo doutras ramas da matemática como a análise matemática, a topoloxía e a xeometría; diferenciándose o estudo que deles fai a álxebra linear no enfoque vectorial deste.
A álxebra linear é moi útil en disciplinas onde se estudan fenómenos mediante modelos lineares[1], caracterizados polas propiedades de aditividade (se unha variábel produce un certo efecto a, e outra variábel produce outro efecto b; a suma das dúas producirá o efecto a+b) e homoxeneidade (ao se multiplicar unha variábel por un número real, o seu efecto multiplicarase por ese mesmo número real).
Estes modelos aparecen en multitude de áreas dentro e fóra das matemáticas. Algúns exemplos[1] son: a análise funcional, as ecuacións en diferenzas, as ecuacións diferenciais lineares,as ecuacións integrais lineares, a programación linear, a investigación de operacións, o cálculo de probabilidades, a informática, a mecánica cuántica, a electrotecnia, o movemento de corpos ríxidos, problemas de frecuencias de vibración de átomos, a enxeñaría, a economía etc.
Historia[editar | editar a fonte]

Os primeiros elementos do que hoxe se coñece como Álxebra lineal acháronse no documento matemático máis antigo que chegou ata os nosos días: o Papiro de Rhind, conservado no Museo Británico (British Museum) -con algúns fragmentos no Museo de Brooklyn (Brooklyn Museum)-, coñecido tamén como o Libro de Cálculo, escrito polo sacerdote exipcio Ahmés cara ao ano 1.650 a.C. Neste valioso documento considéranse as ecuacións de primeiro grao, onde a incógnita aparece representada por un ibis que significa furgando no chan, posibelmente pola súa primoxénica aplicación á agrimensura[2].
Tamén se atopan antecedentes estruturais na álxebra babilónica: a execución da división como a multiplicación dun número polo inverso do divisor leva implícitos rudimentos da Teoría de Grupos[3]. Os matemáticos gregos, pola súa banda, non se van ocupar dos problemas lineares, a pesar de que a solución xeral da ecuación de segundo grao aparece no tratado dos Elementos de Euclides[2].
Os matemáticos chineses durante os séculos III e IV a.C. continúan a tradición dos babilonios e legáronnos os primeiros métodos do pensamento lineal. Na obra Novos capítulos sobre a Arte Matemática de Chuan Tsanom, escrita no ano 152 a.C., durante a Dinastía Han, inclúense sistematicamente todos os coñecementos matemáticos da época. Neste tratado aparece o seguinte sistema linear[2]:
Así como un método para a súa resolución, coñecido como a regra de "fan-chen", a cal en esencia, é o coñecido método de eliminación de Gauss dos nosos días[2].
A álxebra linear tivo un pulo considerábel no mundo islámico, destacando Al-Khwarizmi, quen traduciu ao árabe os textos matemáticos indios e reinterpretou os traballos da escola grega. O seu traballo será a fonte do desenvolvemento da álxebra nos séculos posteriores[4].
Acontecementos cruciais no desenvolvemento da álxebra linear foron: a descuberta dos números complexos como unha extensión dos números reais, e a primeira demostración do nomeado Teorema fundamental da álxebra, o cal afirma que cada polinomio non constante con coeficientes complexos ten polo menos unha raíz complexa. O precursor dos números complexos foi o médico, astrólogo, filósofo e matemático milanés Girolamo Cardano (1501 - 1576)[2].
No século XVII, René Descartes formula problemas de xeometría, como a determinación da intersección de dúas rectas en termos de ecuacións lineares, establecendo desde entón unha ponte entre dúas ramas matemáticas ata entón separadas: a álxebra e a xeometría. Se ben non define a noción básica da álxebra lineal que é a de espazo vectorial, utilízao xa con éxito dun xeito implícito, fundado esencialmente nas ideas xeométricas subxacentes.
Ata o século XVIII a álxebra era, esencialmente, a arte de resolver ecuacións dun grao arbitrario. O matemático e filósofo francés, e un dos iniciadores da Enciclopedia, D'Alembert, descubriu que as solucións dun sistema AX=B forman unha variedade linear. Así mesmo, Euler, Lagrange e o mesmo D'Alembert decátanse de que a solución xeral do sistema homoxéneo AX=0 é unha combinación linear dalgunhas solucións particulares[2].
O seguinte progreso na álxebra linear foi a definición e a análise das primeiras propiedades dos determinantes, que foron usados para a resolución de sistemas de ecuacións lineares. Os determinantes foran xa usados por Leibniz en 1693. Posteriormente, en 1750, Gabriel Cramer ideou a regra de Cramer para resolver sistemas lineares.

É no século XIX cando a álxebra linear adquire relevancia converténdose nunha rama propia das matemáticas. Gauss desenvolve o método de eliminación de Gauss de resolución de sistemas lineares, inicialmente relatado como un avance en xeodesia. Camille Jordan resolve definitivamente o problema da redución dun endomorfismo. En 1843, William Rowan Hamilton (inventor do termo vector) descobre os cuaternións (extensión do corpo dos números complexos) que describen a mecánica en tres dimensións. En 1844, Hermann Grassmann publica seu tratado Die lineale Ausdehnungslehre (A teoría da extensión linear), que é a primeira tentativa de formalización xeral da noción de espazo vectorial. A pesar de pasar desapercibida cando foi publicada, esta obra contén o esencial das ideas modernas da álxebra linear. Grassmann introduce o produto xeométrico e o linear, sendo o primeiro deles o equivalente ao noso produto vectorial; tamén introduce as nocións de independencia linear dun conxunto de vectores, así como a dimensión dun espazo vectorial, e proba a identidade clásica[2]. En 1848 James Joseph Sylvester introduce o termo matriz. Arthur Cayley define a multiplicación de matrices e a matriz inversa mentres estudaba a composición de aplicacións lineares. Aínda que unha matriz está formada por moitos elementos distrbuídos en filas e columnas, Cayley usaba unha única letra para denotar unha matriz. Este feito foi crucial para o desenvolvemento da álxebra matricial. Tamén foi o primeiro en intuír unha conexión entre matrices e determinantes, ao respecto escribiu: "Habería moitas cousas que dicir acerca desta teoría de matrices a cal, paréceme, precedería á teoría dos determinantes". En 1882, Hüseyin Tevfik Pasha usa por primeira vez a denominación Álxebra Linear ao escribir un libro titulado Linear Algebra[5][6]. En 1888, Giuseppe Peano dá a primeira e máis precisa definición de espazo vectorial e axiomatiza enteiramente a teoría. Peano recoñeceu a contribución fundamental de Grassmannn no desenvolvemento da disciplina.
Arredor de 1900 aparece a teoría das aplicacións lineares entre espazos vectoriais de dimensión finita. A álxebra linear adquire a súa forma moderna durante a primeira metade do século XX, cando moitas das ideas e métodos dos séculos precedentes son xeneralizados como álxebra abstracta. Os espazos vectoriais vólvense entón unha estrutura xeral omnipresente en case todos os terreos matemáticos, sobre todo en análise matemática e espazos funcionais. O uso das matrices en mecánica cuántica, relatividade especial e estatística, axuda a espallar a disciplina da álxebra linear máis alá das matemáticas puras. O desenvolvemento dos ordenadores fai incrementar a investigación en algoritmos eficientes para o método de Gauss e a descomposición de matrices, e a álxebra linear convértese nunha ferramenta esencial na modelización e na simulación.
Introdución elemental[editar | editar a fonte]

A álxebra linear ten as súas orixes no estudo dos vectores no espazo cartesiano de dúas e tres dimensións. Un vector, neste caso, é un segmento orientado, caracterizado pola súa lonxitude (ou módulo), a súa dirección e o seu sentido. Os vectores úsanse para representar determinadas entidades físicas como as forzas, e poden sumarse entre eles e multiplicarse por un escalar, formando, xa que logo, o primeiro exemplo de espazo vectorial sobre o corpo dos números reais.
A álxebra linear moderna ampliou o seu campo de estudo para incluír os espazos de dimensión arbitraria ou infinita. Un espazo vectorial de dimensión n chámase n-espazo. Moitos dos resultados dos 2-espazos e 3-espazos poden estenderse aos espazos de dimensión maior. Aínda que moitas persoas non son quen de visualizar facilmente vectores nos n-espazos, estes vectores ou n-uplas son útiles para representar datos, pois poden considerarse como listas ordenadas de n compoñentes. Deste xeito son facilmente comprendidos e manipulados os datos con esta estrutura. Por exemplo, en economía pódese crear un vector 8-dimensional para representar o Produto Interior Bruto (PIB) de 8 estados. Para un ano particular, o PIB dos 8 estados será un 8-vector onde, dada unha certa orde nos países, o PIB dun país concreto será o valor do 8-vector que ocupa a posición correspondente a ese país.
Un espazo vectorial defínese sobre un corpo. Se o corpo é o conxunto dos números reais, teremos un espazo vectorial real; cando o corpo é o dos números complexos, será un espazo vectorial complexo. Unha aplicación linear fai corresponder elementos dun espazo vectorial sobre os elementos doutro espazo vectorial (ou sobre si mesmo), de maneira que se conserve a compatibilidade coa suma e a multiplicación escalar definida no espazo vectorial. O conxunto de todas as aplicacións lineares dun espazo vectorial sobre outro son tamén un espazo vectorial. Fixada unha base para un espazo vectorial, todas as aplicacións lineares sobre ese espazo vectorial poden representarse mediane unha táboa chamada matriz, cuxas propiedades tamén son obxecto de estudo na álxebra linear, así como os algoritmos para calcular as cantidades importantes que as caracterizan como o seu rango, o seu determinante, ou o seu conxunto de autovalores. Un espazo vectorial (ou espazo linear), como concepto puramente abstracto sobre o que se proban teoremas, é parte da álxebra abstracta, e está ben integrado neste campo: algúns obxectos alxébricos relacionados son, por exemplo, o anel das aplicacións lineares dun espazo vectorial en si mesmo, ou o grupo das aplicacións lineares (ou matrices) inversíbeis. A álxebra linear xoga tamén un papel importante na análise matemática, especialmente na descrición das derivadas de orde superior na análise vectorial e na resolución das ecuacións diferenciais.
Concluíndo, pódese dicir simplemente que os problemas lineares da matemática - aqueles que exhiben "linearidade" no seu comportamento - son os máis fáciles de resolver, e que os problemas "non lineares" estúdanse frecuentemente aproximándoos con situacións lineares. Por exemplo na análise matemática, a derivada é unha primeira tentativa de aproximación linear dunha función. A diferenza respecto ao problema non linear é moi importante na práctica: o método xeral de achar unha formulación linear dun problema, en termos de álxebra linear, e resolvelo, se for necesario con cálculo matricial, é un dos métodos máis xerais aplicábeis en matemática.
Nocións básicas[editar | editar a fonte]
Espazo vectorial[editar | editar a fonte]
- Artigo principal: Espazo vectorial.

A noción máis importante en álxebra linear é a de espazo vectorial. Un espazo vectorial é un conxunto de elementos, chamados vectores, con propiedades que os fan semellantes a outros vectores aplicados nun punto fixado (a orixe) do plano ou do espazo.
Máis concretamente, defínense dúas operacións binarias sobre :
- dous vectores e poden sumarse, dando como resultado un novo vector ,
- un vector pode multiplicarse por un escalar, , dando como resultado un novo vector .

O número (chamado escalar) pertence a un corpo fixado desde o comezo: este pode ser, por exemplo o corpo dos números reais ou o corpo dos números complexos.
As dúas operacións deben satisfacer unha longa lista de axiomas. Por exemplo, a suma entre vectores debe ser asociativa e conmutativa. Debe existir un elemento neutro para a suma, que é un vector particular, chamado vector nulo, , tal que para todo vector .
O plano cartesiano é o exemplo fundamental de espazo vectorial. Todo punto do plano identifícase unívocamente cunha dupla de números reais, chamadas coordenadas do punto. A orixe é o punto . O punto pode interpretarse alternativamente como punto do plano ou como vector aplicado na orixe que parte de e remata en ; dise que este vector é o vector de posición do punto .
Analogamente o espazo cartesiano está formado por puntos con tres coordenadas. En xeral, a n-upla de números reais forman un espazo vectorial que se denota por . Máis xeralmente, pódese substituír por outro corpo e obter o espazo vectorial .
Aplicacións lineares[editar | editar a fonte]
- Artigo principal: Aplicación linear.

Unha aplicación linear é unha función entre dous espazos vectoriais
que é compatíbel coas operacións definidas en ambos. Deben cumprirse as seguintes propiedades:
para toda parella de vectores de e todo escalar . Os termos "aplicación", "función", "transformación" e "homomorfismo" son sinónimos neste contexto. O termo "linear" indica a compatibilidade coas operacións. Unha aplicación linear transforma necesariamente a orixe de na orixe de :

Unha aplicación linear dun espazo vectorial en si mesmo dise que é un endomorfismo de . Moitas transformacións do plano cartesiano ou do espazo que teñan invariante a orixe son lineares. Entre estas están: as rotacións en torno ao O, as reflexións respecto dunha recta ou un plano que pasan pola orixe, as homotecias centradas no O e as proxeccións sobre unha recta ou plano que pasen por O.

As aplicacións lineares aparecen en contextos moi diferentes. Por exemplo, o funcional
que asocia a unha función a súa integral é unha aplicación linear
do espazo das funcións continuas de variábel real no intervalo en .
Base e dimensión[editar | editar a fonte]
- Artigos principais: Base (álxebra linear) e Dimensión (espazo vectorial).

Un punto ten dimensión cero, unha recta ten dimensión un, un plano ten dimensión dous. A álxebra linear permite definir e tratar facilmente espazos de dimensión máis alta. O espazo fundamental de dimensión é o espazo vectorial das n-uplas, denotado con . Para , este é o usual plano cartesiano.
Todo espazo vectorial ten unha dimensión, que se define de modo alxébrico como o número de elementos dunha base de : unha base é un conxunto de vectores que actúan como sistema de referencia para . Rigurosamente, unha base é un conxunto
de vectores linearmente independentes que xeran o espazo . Un espazo vectorial pode ter tamén dimensión infinita: os espazos vectoriais de dimensión infinita adoitan ser máis complicados, e moitos teoremas da álxebra linear requiren como hipótese que teña dimensión finita.
As nocións de base e dimensión aplícanse a (que ten dimensión ) e aos subespazos contidos nel. Aínda que definidos dun modo puramente alxébrico, estes conceptos aplícanse tamén en contextos moi diferentes, por exemplo, as matrices forman un espazo vectorial de dimensión . Os polinomios dunha variábel forman un espazo vectorial de dimensión infinita: pero restrinxindo o grao do polinomio a un certo valor máximo , obtense un espazo vectorial de dimensión .
Produto escalar[editar | editar a fonte]
- Artigo principal: Produto escalar.

Dous vectores e dun espazo vectorial poden sumarse: o resultado é un vector . Un vector e un escalar poden multiplicarse: o resultado é un vector . Porén, na definición de espazo vectorial non está prevista unha operación de produto entre dous vectores.
Pero nalgúns contextos é moi útil engadir unha ulterior operación binaria entre vectores que se comporte como un produto. O produto pode definirse de xeito que o resultado sexa ben un número, ou ben un vector. No primeiro caso, a operación é o produto escalar, e no segundo o produto vectorial. Este último só resulta interesante en dimensión tres, mentres que o produto escalar existe (e é útil) en todas as dimensións. Por este motivo, o produto escalar é o máis estudado.
Na definición de espazo vectorial tampouco están previstas as nocións de "lonxitude" (ou "norma") dun vector, e de "ángulo" entre dous vectores. Ambas poden ser definidas se se define un oportuno produto escalar. Máis precisamente, isto sucede nun espazo vectorial dotado dun produto escalar definido positivo.
Aplicacións[editar | editar a fonte]
Sistemas lineares[editar | editar a fonte]
- Artigo principal: Sistema de ecuacións lineares.
Un sistema de ecuacións lineares con incógnitas é da forma:
Onde son as incógnitas, os coeficientes do sistema, e os termos independentes.
O sistema anterior pode expresarse mediante unha igualdade matricial da forma , onde é a matriz de orde cuxa fila i-ésima está formada polos coeficientes da ecuación i-ésima do sistema, é a matriz columna formada polas incógnitas (de orde ), e é a matriz columna formada polos termos independentes (de orde ).
A álxebra linear proporciona moitos algoritmos para calcular as solucións dun sistema linear. A conexión entre os sistemas de ecuacións lineares e a álxebra linear vén dada polo feito de que a matriz , chamada matriz dos coeficientes, pode ser interpretada como aplicación linear de en : segundo esta interpretación, o conxunto das solucións é a contraimaxe de .
O teorema de Rouché-Frobenius permite calcular o número de solucións dun sistema linear, que poden ser ningunha (sistemas incompatíbeis), unha (sistemas compatíbeis determinados) ou infinitas (sistemas compatíbeis indeterminados). No caso de que o sistema teña tantas ecuacións como incógnitas (isto é, a matriz dos coeficientes é cadrada) e que haxa unha única solución, esta pódese calcular usando a regra de Cramer, se ben o gran número de operacións a realizar fanno só utilizábel para sistemas pequenos. Para sistemas grandes son máis efectivos o método de eliminación de Gauss, e os métodos iterativos como o método de Jacobi ou o método de Gauss-Seidel.
Xeometría analítica[editar | editar a fonte]
- Artigo principal: Xeometría analítica.


En xeometría analítica unha recta ou un plano son descritos mediante ecuacións lineares: as posicións relativas de dúas rectas no plano euclídeo (secantes, paralelas ou coincidentes) e dous ou máis planos no espazo euclídeo, poden pescudarse calculando simplemente o número de solucións do sistema linear que forman as ecuacións das rectas ou dos planos. A álxebra linear serve tamén para ver como estas posicións relativas varían ao aplicarlles transformacións lineares.
As cónicas no plano (elipse, hipérbole e parábola) caracterízanse mediante ecuacións de segundo grao, algo máis complicadas cas lineares, de primeiro grao. Non obstante, a clasificación das cónicas realízase dun xeito eficaz cos instrumentos da álxebra linear grazas a algúns teoremas non triviais como o teorema espectral e o teorema de Sylvester. Estes mesmos instrumentos serven para clasificar as cuádricas no espazo.
Cálculo diferencial[editar | editar a fonte]
- Artigo principal: Cálculo diferencial.
A análise matemática das funcións dunha variábel non fan uso da álxebra linear. Pola contra, a análise das funcións en máis variábeis depende fortemente dela. De feito, a noción de derivada esténdese en máis variábeis á de diferencial: mentres a derivada nun punto é un simple número real que indica a pendente dunha función nese punto, a diferencial é unha aplicación linear, que indica sempre a "pendente" dunha función (multivariábel) nun punto.
A noción de derivada segunda esténdese tamén a máis variábeis: o resultado é unha matriz chamada matriz hessiana. Esta matriz é simétrica e pode ser facilmente representada como diagonal grazas ao teorema espectral.
Análise funcional[editar | editar a fonte]
- Artigo principal: Análise funcional.
Moitos problemas da análise funcional, como a busca dunha solución para unha ecuación diferencial, afróntanse analizando un espazo funcional particular. Un espazo funcional, ou espazo de funcións, é un espazo vectorial cuxos elementos son funcións dun certo tipo (por exemplo continuas, integrábeis, derivábeis...) definidas nun dominio fixado. O espazos deste tipo son xeralmente de dimensión infinita, e están dotados dalgunha estrutura adicional, como por exemplo dun produto escalar (nos espazos de Hilbert), dunha norma (nos espazos de Banach) ou dunha máis xeral topoloxía (nos espazos vectoriais topolóxicos).
Exemplos de espazos de funcións son os espazos Lp e os espazos de Sobolev.
Mecánica cuántica[editar | editar a fonte]

- Artigo principal: Mecánica cuántica.
A mecánica cuántica fai amplo uso dos teoremas máis avanzados da álxebra linear. O modelo matemático usado nesta rama da física (formalizado principalmente por Paul Dirac e John Von Neumann) describe os posíbeis estados dun sistema cuántico como elementos dun espazo de Hilbert particular e as magnitudes observábeis (como posición, velocidade etc.) como operadores hermitianos. Os valores que poden tomar estas magnitudes cando realmente se mediron son autovalores do operador.
A introdución e o uso destes conceptos matemáticos non triviais na física cuántica foi un dos maiores estímulos ao desenvolvemento da álxebra linear no século XIX.
Ferramentas[editar | editar a fonte]
Matrices[editar | editar a fonte]
- Artigo principal: Matriz (matemáticas).
Unha matriz é unha táboa de números, como por exemplo:
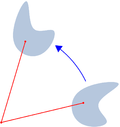
As matrices son útiles en álxebra linear para representar as aplicacións lineares. Isto faise mediante a multiplicación de matrices. Por exemplo, a matriz anterior representa unha transformación do plano cartesiano en si mesmo. Esta transformación aplica o punto no punto
Esta aplicación linear non é outra que a rotación antihoraria de 90º con centro na orixe.
A relación entre matrices e aplicacións lineares é moi forte. Toda aplicación linear entre espazos vectoriais de dimensións e é describíbel por medio dunha matriz asociada de orde , cuxas columnas son as imaxes dos vectores da base do espazo vectorial inicial. O efecto dun cambio de base neste espazo cambia a matriz asociada á aplicación linear. Considerando o cambio de base como un endomorfismo no espazo vectorial cuxa matriz asociada é a do cambio de base, a nova matriz asociada á aplicación linear será o produto da antiga matriz da aplicación pola matriz do cambio de base, pois este produto é a matriz asociada á composición das dúas aplicacións (o endomorfismo e a aplicación linear).
Método de eliminación de Gauss[editar | editar a fonte]
- Artigo principal: Método de eliminación de Gauss.
O método de eliminación de Gauss é un algoritmo que permite transformar unha matriz noutra máis simple mediante as oportunas operacións entre as filas da matriz. Este algoritmo úsase principalmente para determinar as solucións dun sistema de ecuacións lineares, mais ten tamén outras aplicacións na propia álxebra linear: co método de eliminación de Gauss pódese determinar o rango, o determinante ou a inversa dunha matriz, tamén se pode extraer con el unha base dun conxunto de xeradores.
Determinantes[editar | editar a fonte]
- Artigo principal: Determinante (matemáticas).

O determinante é un número asociado a unha matriz cadrada , xeralmente indicado como . Desde un punto de vista alxébrico, o determinante é importante porque vale cero precisamente cando a matriz non é inversíbel; cando non é cero, un método para calcular a matriz inversa fai uso dos determinantes.
Desde un punto de vista xeométrico, o determinante proporciona moita información sobre a transformación asociada a : o seu signo (nos números reais) indica se a transformación mantén a orientación do espazo, e o seu valor absoluto indica como cambian as áreas dos obxectos despois da transformación.
Autovalores e autovectores[editar | editar a fonte]
- Artigo principal: Valor propio, vector propio e espazo propio.

Para caracterizar un endomorfismo é útil estudar algúns vectores, chamados autovectores. Xeometricamente, un autovector é un vector que non cambia de dirección. Desde un punto de vista alxébrico, se trata dun vector tal que
para algún escalar , chamado autovalor. O endomorfismo é particularmente simple de descrivir se é diagonalizábel: xeometricamente, isto quere dicir que existe unha base de autovectores; alxebricamente, quere dicir que o endomorfismo pode ser representado mediante unha matriz diagonal, como por exemplo
Os autovalores poden acharse facilmente calculando o polinomio característico da matriz asociada, definido como
Os autovalores de son precisamente as raíces deste polinomio. Os autovectores organízanse en subespazos vectoriais chamados autoespazos. Cando o espazo vectorial é un espazo de funcións, o autovalor é unha función particular, chamada autofunción.
Forma canónica de Jordan[editar | editar a fonte]
- Artigo principal: Forma canónica de Jordan.
Un endomorfismo diagonalizábel é facilmente representábel mediante unha matriz diagonal. Pero non todos os endomorfismos son diagonalizábeis: por exemplo, unha rotación antihoraria do plano cartesiano de ángulo represéntase pola matriz
que (para distinto de 0 e ) non ten autovalores nin autovectores, e entón a maior razón non pode ser diagonalizábel. Outro exemplo de matriz non diagonalizábel é a seguinte
Pero se o corpo considerado é o corpo dos números complexos, aínda pódese representar o endomorfismo mediante unha matriz que seméllase o máis posíbel a unha matriz diagonal, como no segundo exemplo mostrado. Esta representación, chamada forma canónica de Jordan, caracteriza completamente os endomorfismos. Existe unha representación análoga no corpo real, lixeiramente máis complicada.
Ortogonalización[editar | editar a fonte]
- Artigos principais: Ortogonalización de Gram-Schmidt e Algoritmo de Lagrange.
Dun xeito análogo a un endomorfismo, un produto escalar tamén pode representarse por unha matriz cadrada. Tamén neste contexto, a forma máis simple de tratar é aquela cuxa matriz resulta ser diagonal, e isto ocorre precisamente cando se fixa unha base ortogonal.
A diferenza dos endomorfismos, neste contexto é sempre posíbel achar unha matriz diagonal. Noutras palabras, para calquera produto escalar é posíbel achar unha base ortogonal. Se o produto escalar é definido positivo, un algoritmo eficiente para iso e a ortogonalización de Gram-Schmidt. Para outro produtos escalares pódese usar o algoritmo de Lagrange.
Teoremas[editar | editar a fonte]
Teorema da dimensión[editar | editar a fonte]
- Artigo principal: Teorema da dimensión.
O teorema da dimensión (ou do rango) é un teorema que relaciona as dimensións do núcleo e da imaxe dunha aplicación linear , segundo a fórmula:
Aquí Im e Ker denotan imaxe e núcleo, mentres que é a dimensión do dominio de . Este resultado tamén é chamado teorema do rango, porque traducido á linguaxe matricial asume a forma seguinte:
onde rk e null indican respectivamente o rango e o índice de nulidade dunha matriz de orde .
Teorema de Rouché-Frobenius[editar | editar a fonte]
- Artigo principal: Teorema de Rouché-Frobenius.
O teorema de Rouché-Frobenius proporciona información sobre o conxunto de solucións dun sistema linear:
O teorema afirma dúas cousas:
- o sistema ten solución se e só se a matriz dos coeficientes , e a matriz ampliada (formada engadíndolle a unha columna cos termos independentes) teñen o mesmo rango ;
- se hai solucións, estas forman un subespazo afín de dimensión , onde é o número de incógnitas (que é o número de columnas de ).
En particular, o número de solucións só pode ser cero, un ou infinito (se as ecuacións teñen coeficientes reais ou complexos).
O teorema úsase xeralmente para discutir un sistema, é dicir, para averigüar dun xeito rápido se o sistema é incompatíbel (non ten solución), compatíbel determinado (ten unha solución), ou compatíbel indeterminado (ten infinitas solucións). Porén non se pode usar para calcular as solucións, estas poden calcularse, por exemplo, co método de eliminación de Gauss.
Relación de Grassmann[editar | editar a fonte]
- Artigo principal: Fórmula de Grassmann.
A fórmula de Grassmann relaciona as dimensións de varios subespazos, definidos a partir de dous subespazos e contidos nun espazo fixado . A fórmula é a seguinte:
Na expresión aparecen os subespazos suma e intersección de e .
Teorema espectral[editar | editar a fonte]
- Artigo principal: Teorema espectral.
O teorema espectral proporciona unha condición forte de diagonalizabilidade por algún endomorfismo, chamado endomorfismo simétrico ou hermitiano (ás veces úsase o termo operador como sinónimo de endomorfismo). A noción de endomorfismo simétrico (ou operador hermitiano) depende da presenza dun produto escalar definido positivo (ou produto hermitiano) se se usan espazos vectorias complexos. O teorema espectral asegura que tal endomorfismo ten unha base ortonormal formada por autovectores.
Xeneralización e temas relacionados[editar | editar a fonte]
Os métodos da álxebra linear estendéronse a outras ramas da matemática, grazas ao seu éxito. Na teoría dos módulos substitúese o corpo dos escalares por un anel. A álxebra multilinear ocúpase das funcións que aplican linearmente 'moitas variábeis' nun número diferente de variábeis, levando inevitabelmente ao concepto de tensor. Na teoría espectral dos operadores se traballa con matrices de dimensión infinita aplicando a análise matemática nunha teoría non puramente alxébrica. En todos estes casos son maiores as dificultades técnicas. Ademais, a álxebre linear é fundamental en tódolos ámbitos relacionados coa optimización, en particular na Investigación de Operacións.
Notas[editar | editar a fonte]
- ↑ 1,0 1,1 1,2 Ríos, Sixto (1973). Algebra lineal y geometría vectorial (en castelán). Madrid: FORESA. pp. 5,9. ISBN 84-400-5667-2.
- ↑ 2,0 2,1 2,2 2,3 2,4 2,5 2,6 López Acosta, Norma Patricia (2010). "Antecedentes históricos del Álgebra Lineal" (PDF) (en castelán). Universidad Nacional Autónoma de México. Arquivado dende o orixinal (PDF) o 07 de setembro de 2012. Consultado o 27 de xuño de 2013. Arquivado 07 de setembro de 2012 en Wayback Machine.
- ↑ Castro Gutiérrez, Fernando (1993). "Los orígenes del Álgebra Lineal" (PDF). Suma (en castelán) (Federación Española de Sociedades de Profesores de Matemáticas) (13): 67–68. Arquivado dende o orixinal (PDF) o 08 de outubro de 2013. Consultado o 27 de xuño 2013. Arquivado 08 de outubro de 2013 en Wayback Machine.
- ↑ Rashed, Roshdi (2011). D'Al-Khwarizmi à Descartes. Études sur l'histoire des mathématiques classiques. (en francés). París: Hermann. ISBN 9782705681913. Arquivado dende o orixinal o 24 de setembro de 2019. Consultado o 27 de xuño de 2013. Arquivado 24 de setembro de 2019 en Wayback Machine.
- ↑ Schubring, Gert (2007-06-01). "Hüseyin Tevfik Pasha - The Inventor of ‘Linear Algebra’". Osmanlı Bilimi Araştırmaları (en inglés) 8 (2): 43–48. ISSN 1303-3123.
- ↑ Hüsseyin Tevfik (1882). "Linear Algebra" (en inglés). American Libraries. Consultado o 27 de xuño de 2013.
Véxase tamén[editar | editar a fonte]
| O Galilibros ten un manual sobre: Álxebra lineal |
| Wikimedia Commons ten máis contidos multimedia na categoría: Álxebra lineal |
Bibliografía[editar | editar a fonte]
- Beezer, Rob. A First Course in Linear Algebra (en inglés). licenza GFDL. Consultado o 2 de xullo de 2013.
- de Boor, Carl (2002). Applied Linear Algebra (en inglés). University of Wisconsin-Madison. Consultado o 2 de xullo de 2013.
- Delatorre, Anthony R & Cooke, William K. (1998). Matrix Algebra (en inglés). Monterey, California: Naval Postgraduate School. Consultado o 2 de xullo de 2013.
- Fearnley-Sander, Desmond (1979). "Hermann Grassmann and the Creation of Linear Algebra" (PDF). American Mathematical Monthly (en inglés) 86: 809–817. Consultado o 2 de xullo de 2013.
- Grassmann, Hermann (1844). O. Wigand, ed. Die lineale Ausdehnungslehre ein neuer Zweig der Mathematik: dargestellt und durch Anwendungen auf die übrigen Zweige der Mathematik, wie auch auf die Statik, Mechanik, die Lehre vom Magnetismus und die Krystallonomie erläutert (en alemán). Leipzig. Consultado o 2 de xullo de 2013.
- Lang, Serge (2002). Algebra (en inglés) (3rd ed.). Springer. ISBN 0-387-95385-X.
- Rife, Susan A (1996). Matrix Algebra (en inglés). Monterey, California: Naval Postgraduate School. Consultado o 2 de xullo de 2013.
- Roman, Steven (1992). Advanced linear algebra (en inglés). Springer. ISBN 0-387-97837-2.
- Shafarevich, I. R. (Igorʹ Rostislavovich). Linear algebra and geometry (en inglés). Berlin. ISBN 9783642309939. OCLC 808818333.
- Wedderburn, J. H. M. (1934). Lectures on Matrices (en inglés). Providence: American Mathematical Society. ISBN 0-8218-3204-2. Consultado o 2 de xullo de 2013.
Outros artigos[editar | editar a fonte]
Ligazóns externas[editar | editar a fonte]
- Linear algebra por Elmer G. Wiens (en inglés).
- Linear Algebra Toolkit (en inglés).
- Linear Algebra Workbench: multiplica e inverte matrices, resolve sistemas, acha autovalores etc. (en inglés)
- Linear Algebra en MathWorld (en inglés).




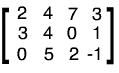
































![{\displaystyle \Psi :C([0,1])\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/68ed84309d7b35cb6ba83d082940007174977575)
![{\displaystyle C([0,1])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44211c4c325ea7edb9462e7ccecda09841a41216)
![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)












































