Parábola (xeometría)

Na Galipedia, a wikipedia en galego.

Unha parábola

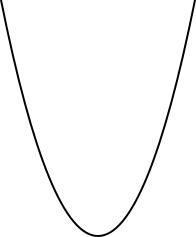
A parábola (do grego: παραβολή) é unha sección cónica xerada pola intersección de unha superficie cónica de segundo grao e un plano paralelo a unha liña xeradora do cono (chamada de xeratriz). Unha parábola tamén pode ser definida como o conxunto dos puntos que son equidistantes dun punto dado (chamado de foco) e dunha recta dada (chamada directriz).

[editar] Definicións

Unha gráfica mostrando as propiedades reflexivas, a directriz (en verde) e as liñas conectando o foco e a directriz coa parábola (en azul)

En coordenadas cartesianas, unha parábola con un eixo paralelo ao eixo y con vértice (h, k), foco (h, k + p), e directriz y = k - p, con p sendo a distancia entre o vértice e o foco, posue a ecuación

ou, alternativamente