Número complexo
| Sistema numérico en matemáticas |
|---|
|
Conxuntos numéricos ℕ ⊂ ℤ ⊂ ℚ ⊂ ℝ ⊂ ℂ |
| Números destacables |
| Outras extensións dos números complexos |
| Infinito |
| Especiais |
| Outros importantes |
| Sistemas de numeración |
Os números complexos son unha extensión dos números reais que teñén estrutura de corpo. O conxunto dos números complexos represéntanse pola letra , cumpríndose que , onde é o conxunto dos números reais.
A necesidade de introducir o conxunto dos números complexos veu dunha gran deficiencia que teñen os números reais: a de que non toda función polinómica ten unha raíz real. O exemplo máis sinxelo é o de que non existe ningún número real x que satisfaga . Esta deficiencia é tan grave que os matemáticos sentiron a necesiadade de inventar un número coa propiedade de que . A introdución deste número "imaxinario" parecía simplificar en gran medida moitos cálculos alxébricos, especialmente cando se admitían os "números complexos" (para ) e se supoñían válidas todas as leis do cálculo aritmético dos números reais[1].
Coa introdución dos números complexos, todas as funcións polinómicas con coeficientes reais teñen raíces (reais ou complexas); ademais o número de raíces coincide co grao da función. Esta propiedade segue a ser válida se os coeficientes son complexos: é o que se coñece como teorema fundamental da álxebra. Como consecuencia desta propiedade, o corpo dos números complexos é alxebricamente pechado.
Os números complexos son a ferramenta de traballo da álxebra ordinaria, chamada álxebra dos números complexos, así como de ramas das matemáticas puras e aplicadas como variábel complexa, aerodinámica e electromagnetismo entre outras de grande importancia.
Conteñen os números reais e os imaxinarios puros e constitúen posibelmente unha das construcións teóricas máis dignas da intelixencia humana. Os análogos do cálculo diferencial e integral con números complexos reciben o nome de análise complexa.
Historia[editar | editar a fonte]
A primeira referencia fugaz á raíz cadrada dun número negativo pode dicirse que quizais ocorreu no traballo do matemático grego do século I Herón de Alexandría, cando na súa obra Stereometrica considerou, aparentemente por erro, o volume dun tronco de pirámide imposíbel, chegando no seus cálculos á expresión . Pero como non se concibían cantidades negativas na matemática helenística, Herón simplemente reemprazouna pola positiva [2].
O pulo no estudo dos números complexos con carácter de seu, xurdiu no século XVI cando matemáticos italianos, como Tartaglia e Cardano, encontraron solucións alxébricas para ecuacións polinómicas de terceiro e cuarto grao. Decatáronse pronto de que estas fórmulas, mesmo se só había solucións reais, requirían ás veces o uso de raíces cadradas de números negativos. Por exemplo, para a ecuación cúbica da forma , Tartaglia atopou que as súas solucións veñen dadas pola fórmula .
A primeira vista, isto parece non ter sentido, porén os cálculos formais con números complexos mostran que a ecuación ten por solucións , e . Substituíndo sucesivamente estas tres solucións por na fórmula de Tartaglia mencionada e simplificando, obtéñense as solucións 0, 1 e −1 como solucións da ecuación . Obviamente, esta ecuación pódese resolver dun xeito máis directo e sinxelo, pero este exemplo ilustra que cando se usan fórmulas xerais (sen utilizar funcións trigonométricas) para resolver ecuacións cúbicas con tres raíces reais distintas, como séculos máis tarde outros matemáticos demostraron rigorosamante[3], o uso dos números complexos é inevitábel. Mesmo esta situación non se pode rectificar factorizando coa axuda do teorema das raíces racionais, se o polinomio cúbico que aparece na ecuación igualado a 0 é irreducíbel (o chamado casus irreducibilis). Este enigma levou a Cardano a concibir os números complexos dun xeito rudimentario, arredor de 1545[4]. Rafael Bombelli foi o primeiro en abordar explicitamente estas solucións aparentemente paradoxais das ecuacións cúbicas, e desenvolveu as regras para a adición, subtracción, multiplicación e extracción de raíces de números complexos[5].
O termo imaxinario para estas cantidades foi acuñado por Descartes en 1637, aínda que estivo a piques de subliñar a súa natureza imaxinaria[6].
Unha posterior fonte de confusión foi que a igualdade semellaba ser caprichosamente inconsistente coa identidade alxébrica , válida para números reais non negativos a e b, e que foi tamén usada en cálculos con números complexos con algún dos a, b real positivo e o outro negativo. O uso incorrecto desta identidade (e tamén da identidade ) no caso en que ambos a e b son negativos, mesmo preocupou a Euler. Esta dificultade levouno á convención de usar o símbolo no canto de para superar este atranco. Aínda así, Euler considerou natural introducir aos estudantes nos números complexos moito antes do que se fai hoxe en día. No seu libro de texto de álxebra elemental, Elementos de Álxebra, introducía estes números case de inmediato e usábaos logo de forma natural.
No século XVIII estendeuse o uso dos números complexos pois se advertiu que a manipulación formal de expresións complexas podería usarse para simplificar os cálculos no que interveñen funcións trigonométricas. Por exemplo, en 1730 Abraham de Moivre observou que as complicadas identidades que relacionan as funcións trigonométricas dun múltiplo enteiro dun ángulo coas potencias das funcións trigonométricas dese ángulo poderían simplemente volverse a expresar mediante a seguinte coñecida fórmula que leva o seu nome, a fórmula de De Moivre: . En 1748, traballando formalmente con series de potencias complexas, Leonhard Euler foi máis alá e obtivo a fórmula de Euler da análise complexa: , observando que esta fórmula podía usarse para reducir calquera identidade trigonométrica a outras identidades exponenciais moito máis simples.
A representación gráfica dos números complexos no plano foi descrita por primeira vez por Caspar Wessel en 1799, aínda que fora anticipada en 1685 por John Wallis no seu De Algebra tractatus. Esta achega de Wessel apareceu nas actas da Real academia de Belas Artes de Dinamarca pero pasaron desapercibidas. Independentemente, en 1806, Jean-Robert Argand publicou un caderniño sobre números complexos e deu unha demostración rigorosa do teorema fundamental da álxebra. Anteriormente Gauss publicara en 1797 unha demostración esencialmente topolóxica deste teorema, mais nese momento expresou as súas dúbidas acerca da "verdadeira metafísica da raíz cadrada de −1". Non foi ata 1831 que superou esas dúbidas e publicou o seu tratado dos números complexos coma puntos no plano[7][8], establecendo en gran medida a notación e a terminoloxía modernas. A comezos do século XIX, outros autores (Buée, Mourey, Warren, os irmáns Français e Bellavitis) descubriron de xeito independente a representación xeométrica dos números complexos[9].

Se ben algúns matemáticos como Abel e Jacobi usaban rutineiramente os números complexos antes da publicación do tratado de Gauss en 1831, o matemático inglés Godfrey Harold Hardy sinala que foi Gauss o primeiro en usar os números complexos 'con confianza e dun xeito científico'[10].
Cauchy e Riemann achegaron ideas fundamentais da análise complexa, elevándoa a un alto estado de acabamento. Un formalismo máis abstracto para os números complexos foi desenvolvido posteriormente por Hamilton, quen estendeu esta abstracción á teoría dos cuaternións.
Os termos comúns usados na teoría débense principalmente aos fundadores. Argand nomeou a o factor dirección, e a o módulo; Cauchy en 1828 chamou a a forma reducida e aparentemente introduciu o termo argumento; Gauss usou para , ideou a forma binómica , e chamou a a norma. A expresión coeficiente de dirección, usada frecuentemente para , débese a Hankel (1867), e valor absoluto para módulo foi idea de Weierstrass.
Escritores clásicos posteriores da teoría dos números complexos son, entre outros: Richard Dedekind, Otto Hölder, Felix Klein, Henri Poincaré, Hermann Schwarz e Karl Weierstrass.
Definición[editar | editar a fonte]
Un número complexo é un par ordenado de números reais; se é un número complexo, dise que a é a parte real de z, , e que b é a parte imaxinaria de z, . O conxunto de todos os números complexos desígnase por .
Se e son dous números complexos, defínense en as operacións internas:
- Suma:
- Produto:
(O + e o que aparecen na esquerda das igualdades son operacións novas que se están definindo, mentres que o + e o que aparecen na dereita representan á suma e ó produto de números reais)[11].
Díxose na introdución que . En realidade, isto non é certo nun sentido estrito pois un número real non é un par ordenado de números reais, porén esta dificultade é menor xa que os números complexos da forma compórtanse respecto á suma e multiplicación de números complexos do mesmo xeito que o fan os números reais respecto á súa suma e multiplicación. En efecto:
Por esta razón convense en designar simplemente por a[11].
Pola contra, os números complexos cuxa parte real é nula, chámanse imaxinarios puros
Dous números complexos son iguais se coinciden as súas partes reais e as súas partes imaxinarias, é dicir:
Unidade imaxinaria. Forma binómica[editar | editar a fonte]
Defínese a unidade imaxinaria, que se representa por , como o número complexo imaxinario puro:
O nome de unidade imaxinaria vén dado polo feito de que calquera número imaxinario puro pode expresarse como o produto da súa parte imaxinaria por . En efecto:
Obsérvese que (a última igualdade xustifícase polo convenio de identificar os números reais cos complexos cuxa parte imaxinaria é nula)[11]. Polo tanto, .
Ademais[12]:
Esta forma de expresar un número complexo, coñécese como forma binómica.
Representación gráfica dos complexos[editar | editar a fonte]

As sucesivas catergorías de números (naturais, enteiros, racionais...) pódense representar sobre a recta. Os números reais énchena por completo de modo que a cada número real lle corresponde un punto da recta e viceversa. É por iso que se fala da recta real.
Para representar os complexos hai que saír da recta e ir ao plano, o plano complexo, chamado así pola mesma razón que a recta real: cada punto do plano representa a un número complexo e viceversa[13].
Tomando uns eixes de coordenadas perpendiculares, no eixe horizontal, ou eixe real, represéntase a parte real do número complexo; e a parte imaxinaria represéntase no eixe vertical, ou eixe [13]. Do mesmo xeito que se representan vectores no plano, a representación dun número complexo é a frecha que une a orixe co punto que determinan ás súas partes reais e imaxinaria. Dito punto chámase afixo do número complexo[14].
Operacións con números complexos[editar | editar a fonte]
A forma binómica é moi útil para realizar operacións con números complexos, sen máis que seguir as regras das operacións dos números reais e tendo en conta que [15].
As operacións xa definidas da suma e a multiplicación, expresadas en forma binómica son:
- Suma:
- Multiplicación:
Os números complexos poden tamén restarse e dividilos (se o divisor non é nulo). Para definir estas operacións necesítase definir o oposto e o conxugado dun número complexo.
O oposto dun número complexo z, que se representa por -z é aquel cuxas partes real e imaxinaria son as opostas das do número dado; así, o oposto de é . O conxugado dun número complexo z, que se representa por , é o que resulta de cambiarlle de signo á parte imaxinaria, é dicir, o complexo conxugado de é [14].
Para restar dous complexos súmaselle ao minuendo o oposto do subtraendo:
- Resta:
Para dividir dous números complexos, multiplícanse o dividendo e o divisor polo conxugado do divisor:
- División:
A potencia dun número complexo pódese facer reiterando a multiplicación do complexo por si mesmo, pero é máis doado facer esta operación, así como a radicación, traballando coa forma polar do complexo.
Forma polar[editar | editar a fonte]
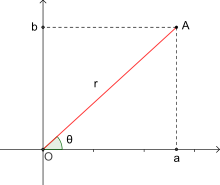
Un xeito alternativo de definir un punto P(x, y) no plano complexo en vez de empregar as coordenadas x e y, é empregar a distancia do punto á orixe de coordenadas O(0, 0), xunto co ángulo entre o eixe positivo real e o vector no sentido positivo (contrario ás agullas do reloxo). Isto conduce á idea da forma polar dos números complexos.
O módulo dun número complexo z é a lonxitude do vector que o representa, o que une a orixe de coordenadas co afixo P(a, b) do complexo. Represéntase por |z|.
O argumento de z é o ángulo que forma o vector que o representa, co eixo real positivo. Escríbese .
Se |z| = r e , o número complexo pódese expresar así: z = rα. Esta é a forma módulo-argumento ou polar dun número complexo[16].
Obsérvese que un número complexo admite infinitos argumentos:
- con (usando graos sesaxesimais).
- con (usando radiáns).
De entre todos eles elíxese por convenio só un está entre 0o e 360o ou entre 0 e 2π radiáns, que é o que se elixe como argumento principal[16][17]. No estudo das funcións de variable complexa séguese o mesmo criterio[18], aínda que algúns autores elixen o argumento principal entre -π e π radiáns (-180o e 180o)[19].
Non ten sentido poñer o número complexo 0 en forma polar[16], mais é común escoller arbitrariamente 0.
Paso da forma binómica á polar[editar | editar a fonte]
Dado o complexo en forma binómica, o módulo de z vén dado polo teorema de Pitágoras: .
O argumento calcúlase tendo en conta que a tanxente do argumento é o cociente entre as partes imaxinaria e real: , polo tanto [16].
Propiedades:
- Se z = a é un número real (é dicir, ), entón o módulo coincide co valor absoluto do número: r = |a|.
- O produto dun complexo polo seu conxugado é igual ao cadrado do módulo, é dicir: .
Paso da forma polar á binómica[editar | editar a fonte]
Dado o complexo z=rα, por trigonometría sábese que: , .
de onde: , .
En consecuencia, a forma binómica do complexo é: .
Sacando factor común, obtense: .
Esta última expresión é o que se coñece como forma trigonométrica do número complexo e serve para pasar da forma polar á binómica[16]. Usando a identidade de Euler pode escribirse .
Operacións con complexos en forma polar[editar | editar a fonte]
A forma polar non é de moita axuda para realizar a suma e a resta de números complexos, porén, para o produto e, en consecuencia, para potencia e a división, a forma polar conduce a un xeito sinxelo de realizaren estas operacións[20].
Produto[editar | editar a fonte]
Para efectuar o produto, primeiramente escríbense os complexos a multiplicar en forma polar, e usando as fórmulas trigonométricas do coseno e o seno da suma de dous ángulos, chégase á expresión en forma polar:
É dicir, o produto de dous complexos é outro complexo cuxo módulo é o produto dos seus módulos e cuxo argumento é igual á suma dos argumentos dos factores:
Unha consecuencia interesante é que se se multiplica un complexo calquera por outro de módulo un , o resultado é xirar en sentido positivo z un ángulo β arredor da orixe.
Potencia[editar | editar a fonte]
Ao elevar un complexo a unha potencia natural, o modulo queda elevado a esa potencia e o argumento queda multiplicado por esa potencia:
pois a potencia non é máis que multiplicar o complexo por si mesmo n veces.
División[editar | editar a fonte]
Para dividir dous complexos divídense os seus módulos e réstanse os seus argumentos:
pois, aplicando a fórmula do produto: .
Fórmula de De Moivre[editar | editar a fonte]
Escribindo en forma trigonométrica o resultado obtido para a potencia dun complexo , obtemos:
Facendo , obtemos a fórmula de De Moivre:
que é moi útil en trigonometría pois permite calcular e , en función de e [21].
Radicación de números complexos[editar | editar a fonte]
Os números reais poden ter dúas, unha ou ningunha raíz real cando o índice da raíz é par, segundo que o número sexa respectivamente positivo, cero ou negativo. No caso de ser o índice impar, existe unha única raíz real. Porén, o número de raíces dos números complexos, agás o 0, é igual ao índice da raíz.
En efecto, sexa un número complexo do que se queren calcular as raíces n-ésimas. Por definición, se entón . Pero como , débense dar as igualdades:
Polo tanto, a raíz n-ésima dun complexo ten por módulo a raíz n-ésima do módulo do complexo e de argumento o seu argumento dividido polo índice n da raíz. Porén, tendo en conta que o argumento dun complexo non é único (podemos obter infinitos argumentos a partir do principal, sumándolle ou restándolle 360º ou 2π radiáns as veces que se queira), a división por n dos distintos argumentos non será o mesmo ángulo. Na expresión anterior, substituíndo β por outro argumento ou , obtéñense n argumentos distintos:
- con ou en radiáns: con
(Obsérvese que para k=n se obtería o mesmo argumento que para k=0, e comezarían a repetirse os argumentos. O mesmo ocorre se se toman valores enteiros negativos de k).
En conclusión, un número complexo ten n raíces complexas, todas elas co mesmo módulo e de argumentos[22]:
- con en graos ou, traballando con radiáns: con .
Estruturas alxébricas[editar | editar a fonte]
Corpo[editar | editar a fonte]
O conxunto dos números complexos coas dúas operacións suma e produto definidas nel, ten estrutura de corpo. En efecto, cúmprense todos os axiomas da definición de corpo[23]:
- é un grupo abeliano:
- 1) A suma é asociativa: ,
- 2) A suma é conmutativa: ,
- 3) O número real é o elemento neutro para a suma: ,
- 4) O elemento oposto do complexo é , pois: ,
- é un grupo abeliano:
- 1) O produto é asociativo: ,
- 2) O produto é conmutativo: ,
- 3) O número real é o elemento neutro para produto (elemento unitario): ,
- 4) O elemento inverso do complexo non nulo é , pois: ,
- O produto é distributivo respecto da suma: ,
Polo tanto é un corpo. É un corpo non ordenado pois non é posible establecer unha relación de orde total en , como ocorre en .
O corpo dos números reais é un subcorpo de , se identificar o número real co complexo .
Espazo vectorial[editar | editar a fonte]
O conxunto dos números complexos é un espazo vectorial real coa operación interna suma de complexos xa definida, e a externa produto por un número real (escalar)[24] definida do seguinte xeito:
- Sexan e , defínese o produto como
Efectivamente, é un espazo vectorial sobre (nótese que se usan os mesmos símbolos + para a suma de complexos e a suma de reais, e para o produto de números complexos e o produto por escalar, e mesmo ambos produtos se expresan sen ningunha notación) xa que verifica os oito axiomas de espazo vectorial:
- 1 a 4) Os catro primeiros axiomas son os que dan a estrutura de grupo abeliano, xa coñecidos pola estrutura de corpo que ten .
- 5) ,
- 6) ,
- 7) ,
- 8) ,
A dimensión deste espazo vectorial é 2. A base canónica é a formada polas unidades real e imaxinaria: .
Notas[editar | editar a fonte]
- ↑ Spivak 1975, p. 639
- ↑ Nahin, Paul J. (2007). An Imaginary Tale: The Story of Sqrt(−1) (en inglés). Princeton University Press. ISBN 978-0-691-12798-9. Arquivado dende o orixinal o 12 de outubro de 2012. Consultado o 11 de abril de 2020.
- ↑ Confalonieri, Sara (2015). The Unattainable Attempt to Avoid the Casus Irreducibilis for Cubic Equations: Gerolamo Cardano's De Regula Aliza (en inglés). Springer. ISBN 3658092750.
- ↑ Kline, Morris (1990). Mathematical Thought From Ancient to Modern Times, volume 1 (en inglés). Oxford University Press. p. 253. ISBN 0199840415.
- ↑ Katz, Victor J. (2004). "sec. 9.1.4". A History of Mathematics, Brief Version (en inglés). Addison-Wesley. ISBN 978-0-321-16193-2.
- ↑ Descartes, René (1954) [1637]. La Géométrie | The Geometry of René Descartes with a facsimile of the first edition (en inglés). Dover Publications. ISBN 978-0-486-60068-0. Consultado o 12 de abril de 2020.
- ↑ Gauss, Carl Friedrich (1831). "Anzeige von Theoria residuorum biquadraticorum, commentatio secunda". Göttingische gelehrte Anzeigen (en alemán). p. 638. Consultado o 12 de abril de 2020.
- ↑ Ewald, William B. (1996). "From Kant to Hilbert: A Source Book in the Foundations of Mathematics" (en inglés). Oxford University Press. p. 313. Consultado o 12 de abril de 2020.
- ↑ Caparrini, Sandro (2000). "On the Common Origin of Some of the Works on the Geometrical Interpretation of Complex Numbers". En Kim Williams. Two Cultures (en inglés). Birkhäuser. p. 139. ISBN 978-3-7643-7186-9. Consultado o 12 de abril de 2020.
- ↑ Hardy, G.H.; Wright, E.M. (2000) [1938]. An Introduction to the Theory of Numbers (en inglés) (4ª ed.). Oxford University Press. p. 189. ISBN 978-0-19-921986-5.
- ↑ 11,0 11,1 11,2 Spivak 1975, p. 647
- ↑ Spivak 1975, p. 648
- ↑ 13,0 13,1 Spivak 1975, p. 650
- ↑ 14,0 14,1 Colera et al. 1995, p. 47
- ↑ Colera et al. 1995, p. 48
- ↑ 16,0 16,1 16,2 16,3 16,4 Colera et al. 1995, p. 50
- ↑ Spivak 1975, pp. 653-654
- ↑ Spivak 1975, pp. 662-663
- ↑ Kasana, H.S. (2005). "1". Complex Variables: Theory And Applications (en inglés) (2ª ed.). PHI Learning Pvt. Ltd. p. 14. ISBN 81-203-2641-5.
- ↑ Colera 1995, p. 52
- ↑ Colera 1995, p. 53
- ↑ Colera 1995, p. 54
- ↑ Spivak 1975, pp. 648-649
- ↑ Negro, A.; Poncela, J.M. (1987). Matemáticas C.O.U. (en castelán). Alhambra. p. 14. ISBN 84-205-1611-2.
Véxase tamén[editar | editar a fonte]
| Wikimedia Commons ten máis contidos multimedia na categoría: Número complexo |
Bibliografía[editar | editar a fonte]
- Ahlfors, Lars (1979). Complex analysis (3rd ed.). McGraw-Hill. ISBN 978-0-07-000657-7.
- Colera, José; de Guzmán, Miguel; Gaztelu, Ignacio; Oliveira, Mª José (1995). Bachillerato. Matemáticas 3 (en castelán). Anaya. ISBN 84-207-6351-9.
- Conway, John B. (1986). Functions of One Complex Variable I. Springer. ISBN 0-387-90328-3.
- Joshi, Kapil D. (1989). Foundations of Discrete Mathematics. Nova York: John Wiley & Sons. ISBN 978-0-470-21152-6.
- Pedoe, Dan (1988). Geometry: A comprehensive course. Dover. ISBN 0-486-65812-0.
- Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007). "Section 5.5 Complex Arithmetic". Numerical Recipes: The Art of Scientific Computing (3rd ed.). Nova York: Cambridge University Press. ISBN 978-0-521-88068-8. Arquivado dende o orixinal o 13 de marzo de 2020. Consultado o 06 de marzo de 2016.
- Spivak, Michael (1975). Calculus (en castelán). Reverté. ISBN 84-291-5141-9.
Outros artigos[editar | editar a fonte]
Ligazóns externas[editar | editar a fonte]
- Introduction to Complex Numbers from Khan Academy
- Euler's Investigations on the Roots of Equations at Convergence. MAA Mathematical Sciences Digital Library.
- John and Betty's Journey Through Complex Numbers
- The Origin of Complex Numbers by John H. Mathews and Russell W. Howell
- Dimensions: a math film.





















































































![{\displaystyle r_{\alpha }\cdot r'_{\beta }=r(\cos \alpha +\mathrm {i} \sin \alpha )\cdot r'(\cos \beta +\mathrm {i} \sin \beta )=r\cdot r'[(\cos \alpha \cos \beta -\sin \alpha \sin \beta )+\mathrm {i} (\sin \alpha \cos \beta +\cos \alpha \sin \beta )]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ffe64c39aef706626ed49f1c7c82a2e5aa8c4ad)
![{\displaystyle =r\cdot r'[\cos(\alpha +\beta )+\mathrm {i} \sin(\alpha +\beta )]=(r\cdot r')_{\alpha +\beta }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f5d6639ac7f4872cb535637f75dea180aed52bd)






![{\displaystyle [r(\cos \alpha +\mathrm {i} \sin \alpha )]^{n}=r^{n}(\cos n\alpha +\mathrm {i} \sin n\alpha )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db58fa75213086ffc5f25e98f7da5a4e779dfa80)







![{\displaystyle {\sqrt[{n}]{R_{\beta }}}=r_{\alpha }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a463050d400bdd11dea02b82b7cadca6f9ca7b6b)

![{\displaystyle R_{\beta }=(r^{n})_{n\alpha }\longrightarrow {\begin{cases}R=r^{n}\rightarrow r={\sqrt[{n}]{R}}\\\\\beta =n\alpha \rightarrow \alpha ={\frac {\beta }{n}}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1f7df706d1d554d1072a013b70119fc9d13979d)





![{\displaystyle r={\sqrt[{n}]{R}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cbca05ffc51ee11a375c341c6bb1bb0f5ab6a91f)

































