Logaritmo

O logaritmo dun número positivo x nunha certa base b, é o expoñente y ao que hai que elevar a base para obter o número dado. A base de logaritmos b ten que ser un número positivo distinto de un.
Abreviadamente o logartimo exprésase por log, indicando a continuación a base como un subíndice e lese "logaritmo en base b de x". Así:
logbx=y se by=x
Por exemplo, o logaritmo de 1000 en base 10 é 3 (log101000=3) pois 103=1000.
Obsérvese que unha igualdade logarítmica vai asociada a unha igualdade exponencial equivalente. Isto débese a que a función logarítmica é a inversa da función exponencial da mesma base para a composición de funcións.
Hai certas bases de logaritmos moi usadas, dando lugar a logaritmos con nome propio. Así:
- Os logaritmos de base 10 chámanse logaritmos vulgares ou decimais. Teñen moitas aplicacións en ciencia e enxeñaría. Adoitase a non escribir a base, así se se escribe logx, enténdese que é o logaritmo decimal de x.
- Os logarimtos de base e levan o nome de logaritmos naturais ou neperianos na honra do introdutor dos logaritmos, o matemático escocés John Napier. Son amplamente usados na matemática pura, especialmente no cálculo infinitesimal. Non se acostuma a usar a expresión habitual, loge, senón ln ou L.
- Os logaritmos de base 2 reciben a denominación de logaritmos binarios e se usan profusamente na ciencia informática. Ademais da notación habitual, log2, úsase tamén lb.
Os logaritmos foron introducidos por John Napier a comezos do século XVII como unha ferramenta para simplificar cálculos. Foron adoptados rapidamente por navegantes, científicos, enxañeiros e outros profesionais para realizar cálculos máis facilmente, usando regras de cálculo e táboas de logaritmos. As tediosas multiplicacións de números con moitas cifras podían facerse cunha simple suma dos logaritmos dos números a multiplicar, cuxos valores mirábanse na táboa de logaritmos; finalmente mirábase na táboa o número cuxo logaritmo era a suma achada, que viña a ser o produto que se buscaba. Isto débese a unha propiedade importante dos logaritmos, a cal di que o logaritmo dun produto é igual á suma dos logaritmos dos factores. Análogas propiedades permiten simplificar os cálculos das divisións, as potencias e as raíces.
A actual notación dos logaritmos ideouna Leonhard Euler no século XVIII ao relacionar as funcións exponencial e logarítmica.
As escalas logarítmicas reducen un amplo rango de cantidades a outras de máis pequeno alcance. Por exemplo, o decibelio é unha unidade logarítmica que mide a presión sonora. En química, o pH dunha solución acuosa é unha medida logarítmica da súa acidez. Os logaritmos son comúns nas fórmulas científicas, na medida da complexidade dun algoritmo informático e na medida dos fractais, describen intervalos musicais, aparecen en métodos de contaxe de números primos, informan sobre algúns modelos en psicofísica, e poden axudar na peritaxe forense.
Do mesmo xeito que a función logarítmica é a inversa da función exponencial, a función logarítmica complexa é a inversa da función exponencial complexa. O logaritmo discreto é outra variante con aplicacións na criptografía de chave pública.
Motivación e definición[editar | editar a fonte]
A idea da operación consistente en calcular logaritmos é a de ser a operación inversa da exponenciación, isto é, a operación de calcular a potencia dun número. Por exemplo, a terceira potencia (ou cubo)de 2 é 8, porque 8 é o produto de tres factores iguais a 2:
Disto séguese que o logaritmo de 8 en base 2 é 3: log2 8 = 3.
Expoñenciación[editar | editar a fonte]
A terceira potencia dun número b é o produto de tres factores iguais a b. Máis xeralmente, elevar b á n-ésima potencia, onde n é un número natural, é multiplicar n factores iguais a b. A n-ésima potencia de b escríbese bn, polo tanto
A expoñenciación pode estenderse a by, onde b é un número positivo e o expoñente y é calquera número real. Por exemplo, b−1 é o inverso ou recíproco de b para a operación da multiplicación, é dicir, é 1/b.
Definición[editar | editar a fonte]
O logaritmo dun número real positivo x con respecta a unha base b positiva e distinta de 1, é o expoñente ao que hai que elevar a base b para obter o número x. Noutras palabras, o logaritmo de x en base b é a solución y da ecuación[1]:
O logaritmo denótase por "logb(x)", léndose "o logaritmo en base b de x". Na ecuación y = logb(x), o valor y é a resposta á pregunta "A que expoñente hai que elevar b para obter x?". Esta cuestión pode tamén formularse (cunha resposta máis enriquecedora) no corpo dos números complexos.
Exemplos[editar | editar a fonte]
Por exemplo, log2(16) = 4, xa que 24 = 2 ×2 × 2 × 2 = 16.
Os logaritmos poden tomar tamén valores negativos, como no exemplo:
pois
Un terceiro exemplo: log10(150) é aproximadamente 2.176, valor comprendido entre 2 e 3 pois 150 áchase entre 102 = 100 cuxo logaritmo é 2, e 103 = 1000 que ten de logaritmo 3.
Finalmente, para calquera base b, logb(b) = 1 e logb(1) = 0, pois b1 = b e b0 = 1, respectivamente.
Identidades logarítmicas[editar | editar a fonte]
- Artigo principal: Lista de identidades logarítmicas.
Algunhas fórmulas importantes, tamén chamadas identidades ou leis logarítmicas, relacionan distintas operacións cos logaritmos[2].
Produto, cociente, potencia e raíz[editar | editar a fonte]
O logaritmo do produto de dous números é igual á suma dos logaritmos de cada factor. O logaritmo do cociente de dous números é a diferenza entre o logaritmo do numerador e o do denominador. O logaritmo dunha potencia é igual ao expoñente multiplicado polo logaritmo da base. O logaritmo dunha raíz é igual ao logaritmo do radicando dividido polo índice da raíz. Estas propiedades están listadas na seguinte táboa con exemplos:
| Fórmula | Exemplo | |
|---|---|---|
| Produto | ||
| Cociente | ||
| Potencia | ||
| Raíz |
Cambio de base[editar | editar a fonte]

O logaritmo logb(x) pode calcularse a partir dos logaritmos de x e b con respecto a unha base arbitraria k usando a seguinte fórmula, coñecida como fórmula do cambio de base:
As calculadoras científicas típicas calculan só logaritmos decimais (base 10) e naturais (base e)[3]. Os logaritmos con respecto a calquera outra base b poden determinarse tomando na fórmula anterior como valor de k calquera das dúas bases que usa a calculadora:
Se na fórmula de cambio de base facemos k=x, obteremos:
de onde, intercambiando os logaritmos, resulta:
elevando a x cada un dos membros desta última igualdade obtense a seguinte expresión:
que permite calcular unha base b descoñecida cando se coñece un número x e o seu logaritmo nesa base, logb(x).
Bases particulares[editar | editar a fonte]
De entre tódalas eleccións posíbeis para a base, tres son as máis xeneralizadas. Son b = 10, b = e (o número irracional de valor aproximado ≈ 2.71828), e b = 2. En análise matemática, o logaritmo de base e úsase amplamente debido á súas particulares propiedades analíticas. Por outro lado, os logaritmos en base 10 son fáciles de usar nas operacións manuais no sistema de numeración decimal, grazas á igualdade[4]: log10(10x)=log10(10)+log10(x)=1+log10(x), deste xeito o logaritmo dun número, log10(x), está relacionado co número de cifras dun enteiro positivo x: o número destas cifras é o enteiro máis pequeno estritamente maior que log10(x)[5]. Por exemplo, o log10(1430) é aproximadamente 3.15. O seguinte enteiro é 4, que é o número de cifras de 1430. O logaritmo en base 2 úsase na ciencia da computación, onde se traballa en sistema binario; e na teoría musical, na que está omnipresente unha proporción tonal de dúas oitavas e o cent é o logaritmo binario da razón entre dous tons (multiplicado por 1200).
A seguinte táboa contén as notacións máis comúns para os logaritmos nestas bases e os campos onde se usan. En moitas disciplinas escríbese log(x) no canto de logb(x) cando a base pode deducirse do contexto. Ás veces aparece a notación blog(x)[6]. A columna "Notación ISO" mostra as designacións recomendadas pola Organización Internacional para a Estandarización (norma ISO 31-11)[7].
| Base b | Nome para logb(x) | Notación ISO | Outras notacións | Usado en |
|---|---|---|---|---|
| 2 | logaritmo binario | lb(x)[8] | ld(x), log(x), lg(x), log2(x) | ciencia da computación, teoría da información, matemáticas, teoría musical |
| e | logaritmo natural ou neperiano | ln(x)[12] | L, log(x) (en matemáticas e en moitas linguaxes de programación[13]) |
análise matemática, física, química, estatística, economía, e algúns campos da enxeñaría |
| 10 | logaritmo decimal ou vulgar | lg(x) | log(x), log10(x) (en enxeñaría, bioloxía, astronomía) |
varios campos da enxeñaría (ex: decibelio), táboas de logaritmos, calculadoras científicas, espectroscopia |
Historia[editar | editar a fonte]
Precedentes[editar | editar a fonte]
Nalgún momento entre o 2000 e o 1600 a.C. os babilonios deberon inventar un algoritmo para multiplicar dous números usando unicamente a suma, a resta e unha táboa das cuartas partes de cadrados de números. O algoritmo di que o produto de dous números é igual á diferenza entre a cuarta parte do cadrado da suma dos dous e a a cuarta parte do cadrado da súa resta[14][15], como facilmente se pode demostrar:
A partir de 1817 elaboráronse grandes táboas de cuartas partes de cadrados de números para poder aplicar este algoritmo, de amplo uso ata a aparición dos ordenadores.
O matemático indio Virasena traballou co concepto de ardhaccheda: o número de veces que se pode facer a metade dun número da forma 2n. Para as potencias de 2 é o logaritmo do número, cuxo valor é enteiro; para outros números, é indefinido. Describiu relacións como a fórmula do logaritmo do produto e tamén introduciu os logaritmos enteriron en base 3 (trakacheda) e en base 4 (caturthacheda)[16]
En 1544, Michael Stifel publicou en Nuremberg Arithmetica integra, onde aparecía unha táboa de enteiros e potencias de 2[17] que está considerada como unha versión temperá dunha táboa de logaritmos[18][19].
Nos séculos XVI e XVII usábase un algoritmo para aproximar a multiplicación e a división, chamado prosthaphaeresis, que usaba a identidade trigonométrica
ou outra similar para converter multiplicacións e divisións en consultas nunha táboa. Porén, os logaritmos son máis directos e requiren menos traballo. Usando a fórmula de Euler pode mostrarse que as dúas técnicas están relacionadas.
De Napier a Euler[editar | editar a fonte]

O método de logaritmos naturais foi proposto inicialmente en 1614, nun libro titulado Mirifici Logarithmorum Canonis Descriptio (Descrición da marabillosa regra dos logaritmos), por John Napier[20] (latinizado Neperus), Barón de Merchiston en Escocia, que naceu en Edimburgo en 1550, e morreu na mesma cidade en 1617. Joost Bürgi, un matemático e reloxeiro suízo, ó servizo do Duque de Hesse-Kassel, concibiu por vez primeira os logaritmos, mais publicou os seus achados seis anos despois que Napier[21].
Johannes Kepler, quen usou as táboas de logaritmos extensivamente para compilar a súa obra Ephemeris, dedicada a Napier[22], sinalou:
...o acento no cálculo guiou a Justus Byrgius (Joost Bürgi) no camiño cara a estes logaritmos moitos anos antes de que aparecera o sistema de Napier; pero... no canto de amosar o neno para o beneficio público desertou del no nacemento.-Johannes Kepler[23],Rudolphine Tables (1627)

Mediante sucesivas restas Napier calculou (1 − 10−7)L para L desde 1 a 100. O resultado para L=100 é aproximadamente 0.99999 = 1 − 10−5. Napier calculou entón os produtos deses números con 107(1 − 10−5)L para L desde 1 a 50, e fixo o mesmo con 0.9998 ≈ (1 − 10−5)20 e 0.9 ≈ 0.99520. Estes cálculos, que lle ocuparon 20 anos, permitíronlle dar, para calquera número N desde 5 a 10 millóns, o número L que é solución da ecuación:
Nun principio, Napier chamou a L "número artificial", pero máis tarde púxolle o nome "logaritmo" para significar un número que indica unha proporción: do grego λόγος (logos), proporción, e ἀριθμός (arithmos), número [24]. En notación moderna, a relación para os logaritmos naturais é:
onde a aproximación máis próxima corresponde á observación de que:
A invención foi rápida e amplamente aclamada. Os traballos de Bonaventura Cavalieri (Italia), Edmund Wingate (Francia), Xue Fengzuo (China) e o Chilias logarithmorum de Johannes Kepler (Alemaña), axudaron en gran medida a espallar o concepto[25].

En 1647 Grégoire de Saint-Vincent relacionou os logaritmos coa cuadratura da hipérbole, sinalando que a área f(t) baixo a hipérbole desde x = 1 a x = t satisfai:
O logaritmo natural foi inicialmente descrito por Nicholas Mercator no seu traballo Logarithmotechnia publicado en 1668[26], aínda que o profesor de matemáticas John Speidell xa tiña compilada en 1619 unha táboa de logaritmos naturais[27]. Arredor de 1730, Leonhard Euler definiu as funcións exponencial e logarítmica como:
Euler tamén demostrou que as dúas funcións son inversas unha da outra[21][25][28].
Táboas de logaritmos, regras de cálculo e aplicacións históricas[editar | editar a fonte]

Coa simplificación dos cálculos, os logaritmos contribuíron ó avance da ciencia, e especialmente da astronomía. Foron fundamentais no avance da agrimensura, a navegación, e outras disciplinas. Pierre Simon Laplace chamou aos logaritmos:
... unha admirábel ferramenta que, ao reducir a uns poucos días o labor de moitos meses, dobra a vida do astrónomo e líbrao dos erros e frustracións inseparábeis dos cálculos longos.Pierre Simon Laplace[29].
Unha ferramenta fundamental que permitía o uso práctico dos logaritmos antes da aparición das calculadoras e os ordenadores foi a "táboa de logaritmos"[30]. A primeira táboa foi compilada por Henry Briggs en 1617, inmediatamente despois da invención de Napier. Subsecuentemente, apareceron táboas con alcance e precisión cada vez maiores. Estas táboas listaban valores de logb(x) e bx para calquera número x nun certo rango, cunha certa precisión, e para unha certa base b (xeralmente b = 10). Por exemplo, a primeira táboa de Briggs contiña os logaritmos vulgares de tódolos enteiros comprendidos entre 1 e 1000, cunha precisión de 8 díxitos. Como a función f(x) = bx é a función inversa de logb(x), foi chamada a función antilogaritmo[31]. O produto e o cociente de dous números positivos c e d eran calculados rutineiramente como a suma e a diferenza dos seus logaritmos. O produto cd ou o cociente c/d obtíñanse mirando na mesma táboa o antilogaritmo da suma ou da diferenza respectivamente:

e
Para facer cálculos manuais que demandaban unha precisión considerábel, mirar os logaritmos nas táboas dos dous números, calcular a suma ou a resta dos logaritmos, e finalmente buscar na mesma táboa o antilogaritmo deste último número, era un método moito máis rápido de facer multiplicacións e divisións ca executar os primitivos métodos de multiplicar ou dividir, como a prosthaphaeresis, baseada nas identidades trigonométricas. Os cálculos de potencias e raíces reducíanse a multiplicacións e divisións e buscas na táboa por:
e
Moitas táboas de logaritmos dábanos separando a característica e a mantisa de x, é dicir, a parte enteira e a parte fraccionaria de log10(x)[32]. A característica de 10 · x é igual á característica de x máis 1, e as súas mantisas son iguais. Este feito amplía a táboa dos logaritmos dos números do 1 ao 1000 a máis números, por exemplo o logaritmo de 3542 aproxímase por:
Durante os séculos XIX e XX foron moi usadas en España as táboas de logaritmos do matemático e político galego Vicente Vázquez Queipo. Foron declaradas oficialmente "libro de texto" e só coa chegada das calculadoras na década dos setenta, caeron en desuso.
Outra aplicación crítica dos logaritmos foi a regra de cálculo, formada por un par de regras cunha escala logarítmica que se deslizan unha sobre a outra, usada para cálculos como o que se explica na seguinte ilustración.

A escala logarítmica non deslizante, regra de Gunter, foi inventada pouco despois do descubrimento de Napier. William Oughtred mellorouna para crear a regra de cálculo, un par de escalas logarítmicas deslizantes unha con respecto da outra. Os números sitúanse a distancias proporcionais ás diferenzas entre os seus logaritmos. Deslizar a escala superior apropiadamente equivale a engadir mecanicamente os logaritmos. Por exemplo, engadindo á distancia de 1 a 2 na escala inferior, a distancia de 1 a 3 na escala superior, dá como resultado un produto de 6, o cal lese na parte inferior. A regra de cálculo foi unha ferramenta esencial de cálculo para enxañeiros e científicos ata os anos setenta do século XX porque permitía, a expensas da precisión, uns cálculos moito máis rápidos cas técnicas baseadas nas táboas[25].
Logaritmo neperiano[editar | editar a fonte]
En cálculo chámase logaritmo natural ou logaritmo neperiano á primitiva da función inversa definida como:
a cal toma o valor 0 cando a variable x toma o valor 1, é dicir:
Tamén se chama así ó logaritmo obtido tomando como base o valor de número irracional "e" (equivalente a 2,718281828...).
Equivalentemente, a función logaritmo natural é a inversa da función exponencial definida por : .
Dedución[editar | editar a fonte]
A derivada da función é . Ó dividir ambos lados da expresión por "n" e observar o resultado, pódese afirmar que unha primitiva de é (con m = n - 1). Este cálculo obviamente non é válido cando m = - 1, porque non se pode dividir por cero. Polo tanto, a función inversa 1/x é a única función "potencia" que non ten unha primitiva "potencia". Pero esta función é continua sobre o rango ]0; + ∞[ o que implica que ten forzosamente unha primitiva neste intervalo, e tamén sobre ] - ∞ ; 0[.
En resumo: , e .
A función é estritamente crecente pois a súa derivada é estritamente positiva, e ten límites infinitos en 0+ y en + ∞.
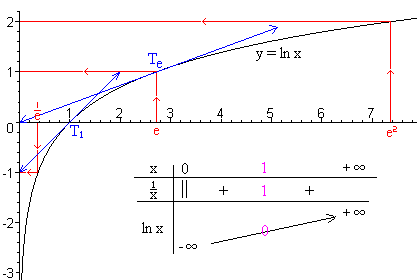
A tanxente Te que pasa polo punto de abscisa e da curva, pasa tamén pola orixe.
A tanxente T1 que pasa polo punto de abscisa 1 da curva, ten como ecuación: y = x - 1.
A derivada de segundo orde é ln"(x) = -1 / x², sempre negativa, polo tanto a función é cóncava, é dicir que tódalas tanxentes pasan por riba da curva. É o que se constata con T1 e Te.
Características útiles[editar | editar a fonte]
- Os números positivos menores que 1 teñen logaritmo negativo.
- Os números positivos maiores que 1 teñen logaritmo positivo.
- Os números negativos teñen logaritmo complexo.
- Non existen os logaritmos en base negativa.
Propiedade fundamental[editar | editar a fonte]
A denominada propiedade fundamental, definida por:
(1) (con a>0 e b>0)
foi a que permitiu construír as primeiras táboas de logaritmos, cuxo propósito era facer que calcular un produto fose tan rápido como atopar unha suma. En efecto, para calcular un produto procurábanse na táboa os logaritmos dos factores, sumábanse, e procurábase o número cuxo logaritmo aproximábase máis á expresión ln a + ln b. A hoxe desaparecida regra de cálculo utilizaba o mesmo proceso.
Proba: Sexa f(x) = ln (ax) - ln x. Derivando: f'(x) = a·(1/ax) - 1/x = 1/x - 1/x = 0, o que significa que f é constante no intervalo (0, + ∞). En consecuencia f(b) = f(1), é dicir: ln ab - ln b =ln a -ln 1, ou sexa ln ab= ln a + ln b.
consecuencias:
- ln (1/a) = - ln a. (2)
En efecto, ln(a) + ln (1/a) = ln (a· 1/a) =ln 1= 0.
- ln (a/b) = ln a - ln b. (3)
En efecto ln (a/b) = ln (a·1/b) = ln a + ln (1/b) = ln a - ln b.
- ln (an) = n.ln a. (4) , para calquera valor real de n.
Isto demóstrase por indución para todo número enteiro natural "n", e logo para todo "n" enteiro, con (2), e logo para todo "n" racional, utilizando (3). A continuidade do logaritmo fai que unha relación certa nos racionais é tamén válida nos reais, o que acaba a proba.
Esta última relación permite resolver certas ecuacións coa incógnita no lugar das potencias: ax =b ten como solución x= lnb/lna cando a ≠ 1, a>0 e b>0.
Notas[editar | editar a fonte]
- ↑ Kate, S.K.; Bhapkar, H.R. (2009). "capítulo 1". En Technical Publications. Basics Of Mathematics (en inglés). Pune. ISBN 978-81-8431-755-8. Arquivado dende o orixinal o 12 de xaneiro de 2014. Consultado o 31 de decembro de 2013.
- ↑ Todas as fórmulas desta sección poden verse en calquera libro de matemáticas elementais, por exemplo en Shirali, Shailesh (2002). "sección 4". En Hyderabad Universities Press. A Primer on Logarithms (en inglés). ISBN 978-81-7371-414-6., en Downing, Douglas (2003). "capítulo 17". En Barron´s. Algebra the Easy Way. Barron's Educational Series (en inglés). Hauppauge, N.Y. p. 275. ISBN 978-0-7641-1972-9., ou en Kate, S.K.; Bhapkar, H.R. (2009). "capítulo 1". En Technical Publications. Basics Of Mathematics (en inglés). Pune. ISBN 978-81-8431-755-8. Arquivado dende o orixinal o 12 de xaneiro de 2014. Consultado o 31 de decembro de 2013.
- ↑ Bernstein, Stephen; Bernstein, Ruth (1999). McGraw-Hill, ed. Schaum's outline of theory and problems of elements of statistics. I, Descriptive statistics and probability. Schaum's outline series (en inglés). Nova York. p. 21. ISBN 978-0-07-005023-5.
- ↑ Downing, Douglas (2003). "capítulo 17". En Barron´s. Algebra the Easy Way. Barron's Educational Series (en inglés). Hauppauge, N.Y. p. 275. ISBN 978-0-7641-1972-9.
- ↑ Wegener, Ingo (2005). Springer-Verlag, ed. Complexity theory: exploring the limits of efficient algorithms (en inglés). Berlin, New York. p. 20. ISBN 978-3-540-21045-0.
- ↑ Franz Embacher; Petra Oberhuemer. mathe online: für Schule, Fachhochschule, Universität unde Selbststudium, ed. "Mathematisches Lexikon" (en alemán). Consultado o 1 de xaneiro de 2014.
- ↑ B. N. Taylor (1995). US Department of Commerce, ed. "Guide for the Use of the International System of Units (SI)" (en inglés). Arquivado dende o orixinal o 29 de xuño de 2007. Consultado o 02 de xaneiro de 2014.
- ↑ Gullberg, Jan (1997). W. W. Norton & Co, ed. Mathematics: from the birth of numbers. (en inglés). Nova York. ISBN 978-0-393-04002-9.
- ↑ Paul Halmos (1985). Springer-Verlag, ed. I Want to Be a Mathematician: An Automathography (en inglés). Berlin, New York. ISBN 978-0-387-96078-4.
- ↑ Irving Stringham (1893). The Berkeley Press, ed. Uniplanar algebra: being part I of a propædeutic to the higher mathematical analysis (en inglés). p. xiii.
- ↑ Roy S. Freedman (2006). Academic Press, ed. Introduction to Financial Technology (en inglés). Amsterdam. p. 59. ISBN 978-0-12-370478-8.
- ↑ Algúns matemáticos desaproban esta notación. Paul Halmos, na súa autobiografía de 1985, criticaba o que el consideraba a "pueril notación ln", que, dicía, ningún matemático usou xamais.[9] A notación inventouna Irving Stringham, un matemático.[10][11]
- ↑ Por exemplo C, Java, Haskell, e BASIC.
- ↑ McFarland, David (2007). "Quarter Tables Revisited: Earlier Tables, Division of Labor in Table Construction, and Later Implementations in Analog Computers" (en inglés). p. 1.
- ↑ Robson, Eleanor (2008). Mathematics in Ancient Iraq: A Social History (en inglés). p. 227. ISBN 978-0691091822.
- ↑ Gupta, R. C. (2000). Popular Prakashan, ed. Students' Britannica India: Select essays (en inglés). p. 329.
- ↑ Stifelio, Michaele (1544). Iohan Petreium, ed. Arithmetica Integra (en latín). Londres.
- ↑ Bukhshtab, A.A.; Pechaev, V.I. (2001). "Arithmetic". En Hazewinkel, Michiel. Encyclopedia of Mathematics (en inglés). Springer. ISBN 978-1-55608-010-4.
- ↑ Vivian Shaw Groza e Susanne M. Shelley (1972). Holt, Rinehart and Winston, ed. Precalculus mathematics (en inglés). Nova York. p. 182. ISBN 978-0-03-077670-0.
- ↑ Ernest William Hobson (1914). Cambridge University Press, ed. John Napier and the invention of logarithms, 1614 (en inglés). Cambridge.
- ↑ 21,0 21,1 Boyer, Carl B. (1991). John Wiley & Sons, ed. A History of Mathematics (en inglés). Nova York. pp. =484, 489. ISBN 978-0-471-54397-8.
- ↑ Gladstone-Millar, Lynne (2003). National Museums Of Scotland, ed. John Napier: Logarithm John (en inglés). p. 44. ISBN 978-1-901663-70-9.
- ↑ Napier, Mark (1834). William Blackwood, ed. Memoirs of John Napier of Merchiston (en inglés). Edimburgo. p. 392.
- ↑ William Harrison De Puy (1893). Werner Co., ed. The Encyclopædia Britannica: a dictionary of arts, sciences, and general literature ; the R.S. Peale reprint (en inglés) 17 (9ª ed.). p. 179.
- ↑ 25,0 25,1 25,2 Maor, Eli (2009). "1, 2, 13". En Princeton University Press. e: The Story of a Number (en inglés). ISBN 978-0-691-14134-3.
- ↑ J. J. O'Connor; E. F. Robertson (Setembro de 2001). The MacTutor History of Mathematics archive, ed. "The number e". Consultado o 30/12/2013.
- ↑ Cajori, Florian (1991). AMS Bookstore, ed. A History of Mathematics (en inglés) (5ª ed.). Providence, RI. p. 152. ISBN 978-0-8218-2102-2.
- ↑ Eves, Howard Whitley (1992). "9-3". En Saunders. An introduction to the history of mathematics. The Saunders series (en inglés) (6ª ed.). Filadelfia. ISBN 978-0-03-029558-4.
- ↑ Bryant, Walter W. Methuen & Co, ed. A History of Astronomy (en inglés). Londres. p. 44.
- ↑ Campbell-Kelly, Martin (2003). "sección 2". En Oxford University Press. The history of mathematical tables: from Sumer to spreadsheets. Oxford scholarship online (en inglés). ISBN 978-0-19-850841-0.
- ↑ Abramowitz, Milton; Stegun, Irene A., eds. (1972). "sección 4.7". Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables (en inglés) (10ª ed.). Nova York: Dover Publications. p. 89. ISBN 978-0-486-61272-0.
- ↑ Spiegel, Murray R.; Moyer, R.E. (2006). McGraw-Hill, ed. Schaum's outline of college algebra. Schaum's outline series (en inglés). Nova York. p. 264. ISBN 978-0-07-145227-4.
Véxase tamén[editar | editar a fonte]
| Vexa a entrada do Galizionario acerca de logaritmo |
| Commons ten máis contidos multimedia sobre: Logaritmo |












![{\displaystyle \log _{b}{\sqrt[{n}]{x}}={\frac {\log _{b}(x)}{n}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/835928927072f0d6c3911a1b4a0b92ace5dcd8aa)







![{\displaystyle \cos \,\alpha \,\cos \,\beta ={\frac {1}{2}}[\cos(\alpha +\beta )+\cos(\alpha -\beta )]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55be02a407ad9d4127584bd6d02f3fde6ac05fb9)









![{\displaystyle {\sqrt[{d}]{c}}=c^{\frac {1}{d}}=b^{{\frac {1}{d}}\log _{b}(c)}.\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ba9e10fbda0f1ce9dd2d211ec6bc2c80d1f3dd8)











