Presión sonora
A presión sonora ou acústica é a variación local de presión con respecto da presión atmosférica do ambiente causada por unha onda sonora. A presión sonora no ar pódese medir mediante un micrófono, mentres que na auga pódese facer mediante un hidrófono. A unidade do SI para a presión sonora p é o pascal (síbolo: Pa).

O nivel de presión sonora (SPL, Sound pressure level) ou nivel sonoro é unha medida logarítmica da presión sonora eficaz dun son relacionándoa cun valor de referencia. Mídese en decibelios (dB) sobre un nivel estándar de referencia. A presión de referencia "cero" comunmente empregada no aire son 20 µPa RMS, que se considera o limiar de audición humano (a 1 kHz). Esta é a unidade que empregan os sonómetros para expresar a intensidade dun son.
Presión sonora instantánea[editar | editar a fonte]
A presión sonora instantánea é a variación da presión ambiental local nun punto e tempo dados.
A presión sonora eficaz é o valor eficaz da presión sonora instantánea nun intervalo de tempo ou espazo.
A presión sonora total vén dada por:
onde:
- = presión atmosférica (aire) ambiental local,
- = desviación da presión sonora.
Intensidade[editar | editar a fonte]
Nunha onda sonora, a variable complementaria coa presión sonora é a velocidade de partícula acústica. Conxuntamente determinan a intensidade acústica da onda. A intensidade sonora instantánea é o produto da presión sonora e a velocidade da partícula acústica.
Impedancia acústica[editar | editar a fonte]
Para pequenas amplitudes, a presión sonora e a velocidade de partícula están relacionadas linearmente mediante a impedancia acústica. A impedancia acústica depende pois destas dúas características da onda así como do medio de transmisión.
A impedancia acústica vén dada por:[1]
onde
- Z é a impedancia sonora
- p é a presión acústica
- U é a velocidade de partícula
Desprazamento de partícula[editar | editar a fonte]
A presión sonora p está ligada co desprazamento de partícula (ou amplitude de partícula) ξ por
- .
A presión sonora p é
- ,
normalmente coas unidades N/m² = Pa.
onde:
| Símbolo | Unidade do SI | Significado |
|---|---|---|
| p | pascais | presión sonora |
| f | hertz | frecuencia |
| ρ | kg/m³ | densidade do aire |
| c | m/s | velocidade do son |
| v | m/s | velocidade da partícula |
| = 2 · · f | radiáns/s | frecuencia angular |
| ξ | metros | desprazamento da partícula |
| Z = c • ρ | N·s/m³ | impedancia acústica |
| a | m/s² | aceleración da partícula |
| I | W/m² | intensidade do son |
| E | W·s/m³ | densidade de enerxía sonora |
| Pac | watts | potencia acústica |
| A | m² | área |
Lei da distancia[editar | editar a fonte]
Cando se mide o son creado por unha fonte, é importante tamén medir a súa distancia con respecto a esta, pois a presión sonora decrece cunha cunha relación de 1/r (e non 1/r2, como a intensidade sonora).
A lei da distancia para unha presión sonora p en 3D di que esta é inversamente proporcional á distancia r dunha fonte puntual sonora.
Se a presión sonora , é medida a unha distancia , pódese calcular a presión sonora noutra posición ,
A presión sonora pode variar segundo a dirección. Un exemplo obvio é un megáfono.
Nivel de presión sonora[editar | editar a fonte]
O nivel de presión sonora (SPL) ou nivel sonoro é unha medida logarítmica da presión sonora eficaz dun son relacionada cun valor de referencia. Mídese en decibelios (dB) sobre un nivel de referencia estándar.
onde é o nivel de presión de referencia E é o valor de presión eficaz que se está a medir.[2][3]
Ás veces empréganse variantes tales como dB (SPL), dBSPL, ou dBSPL, mais non están recoñecidas como unidade no SI. A unidade dB (SPL) é moitas veces abreviada a "dB", o que pode dar a impresión errónea de que se trata dunha unidade por si mesma.
A presión sonora comunmente empregada no aire son = 20 µPa (rms), que se considera o limiar de audición (aproximadamente o voar dun mosquito a tres metros). A maioría das medidas do nivel sonoro fanse respecto a esta referencia, dando que 1 pascal equivale un nivel de presión sonora de 94 dB. Noutros medios, como na auga, emprégase o nivel de referencia de 1 µPa.[4] Estas referencias están definidas polo ANSI S1.1-1994.
A distancia do micrófono de medición da fonte sonora é normalmente omitida cando se miden SPLs, facéndoos inútiles. No caso de medidas de ruídos ambientais de fondo, non se anota a distancia pois non hai unha soa fonte sonora, senón varias, pero cando se mide o nivel sonoro dunha fonte específica, é precisa a distancia, empregándose normalmente como valor estándar a distancia de 1 metro. Pola razón dos sons reflectidos dentro dun local, para comparar distintos equipos hai que facer uso dunha cámara anecoica.
O límite inferior da audición é o limiar definido como o SPL de 0 dB, mais o límite superior non está tan claramente definido. Mentres 1 atm (SPL de 194 dB) é a maior variación de presión que unha onda sonora pode ter na atmosfera terrestre, pódense presentar ondas sonoras maiores noutras atmosferas ou noutros medios tales como a auga ou a terra.
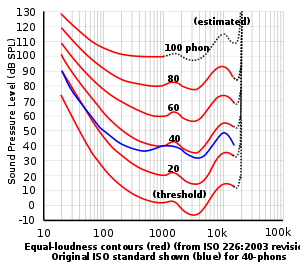
Os oídos detectan os cambios de presión sonora, mais a audición non se corresponde a unha sensibilidade espectral plana (resposta en frecuencia) en relación á frecuencia e á amplitude. Os humanos non perciben os sons de baixa e alta frecuencia tan ben como os sons de arredor dos 3.000 Hz, como amosan as curvas isofónicas.
Para distinguir entre diferentes medicións, empréganse os sufixos A, B, e C, para medir, respectivamente sons inferiores a 55 dB, dos que van de 55 dB até 85 dB, e os superiores a estes, tendo, por conseguinte, dBA ou LA, dBB ou LB, e dBC ou LC. Os niveis de presión sonora sen ningunha ponderación denomínanse "niveis de presión sonora lineares", que son normalmente escritos como dBL ou simplemente L. Algúns instrumentos de medición empregan a letra Z para indicar os SPL lineares.
Suma de niveis[editar | editar a fonte]
A fórmula para a suma total de niveis de presión sonora de n fontes de radiación incoherentes é
Da fórmula do nivel da presión sonora temos que
E substituíndo temos logo que
Notas[editar | editar a fonte]
- ↑ "What is acoustic impedance and why is it important?" (en inglés). Consultado o 9 de maio de 2012.
- ↑ Bies, David A., and Hansen, Colin. (2003). Engineering Noise Control.
- ↑ A presión de referencia pódese denotar como p0, para non confundila coa presión ambiental (moito máis alta).
- ↑ C. L. Morfey, Dictionary of Acoustics (Academic Press, San Diego, 2001).
Véxase tamén[editar | editar a fonte]
Bibliografía[editar | editar a fonte]
- Beranek, Leo L, "Acoustics" (1993) Acoustical Society of America. ISBN 0-88318-494-X
- Morfey, Christopher L, "Dictionary of Acoustics" (2001) Academic Press, San Diego.
Ligazóns externas[editar | editar a fonte]
- Sound pressure and Sound power – Effect and Cause
- Conversion of sound pressure to sound pressure level and vice versa
- Table of Sound Levels - Corresponding Sound Pressure and Sound Intensity
- Ohm's law as acoustic equivalent - calculations
- Definition of sound pressure level
- A table of SPL values
- Relationships of acoustic quantities associated with a plane progressive acoustic sound wave - pdf
- Sound pressure and sound power - two commonly confused characteristics of sound
- How many decibels is twice as loud? Sound level change and the respective factor of sound pressure or sound intensity
- Decibel (loudness) comparison chart
























