Número áureo

O número áureo ou número de ouro (tamén chamado número prateado, razón extrema e media,[1] razón áurea, razón dourada, media áurea, proporción áurea e divina proporción) representado pola letra grega φ (fi) (en honor ao escultor grego Fidias), é o número irracional:[2]
Trátase dun número alxébrico que posúe moitas propiedades interesantes e que foi descuberto na antigüidade, non como “unidade” senón como relación ou proporción entre segmentos de rectas. Esta proporción encóntrase tanto nalgunhas figuras xeométricas como na natureza en elementos tales como caracois, nervios das follas dalgunhas árbores, o grosor das ramas etc.
Así mesmo, atribúeselle un carácter estético especial aos obxectos que seguen a razón áurea, así como unha importancia mística. Ao largo da historia, atribuíuselle importancia en diversas obras de arquitectura e outras artes, aínda que algúns destes casos foron obxectables para as matemáticas e a arqueoloxía.
Definición[editar | editar a fonte]
| Números γ - ζ(3) - √2 - √3 - √5 - φ - α - e - π - δ | |
| Binario | 1,1001111000110111011... |
| Decimal | 1,6180339887498948482... |
| Hexadecimal | 1,9E3779B97F4A7C15F39... |
| Fracción continua | |
| Alxébrico | |
Dise que dous números positivos a e b están en razón áurea se e só se:
Para obter o valor de a partir desta razón considere o seguinte:
Que a lonxitude do segmento máis curto b sexa 1 e que a de a sexa x.
Para que estes segmentos cumpran coa razón áurea deben cumprir que:
Multiplicando ambos lados por x e reordenando:
Mediante a fórmula xeral das ecuacións de segundo grao obtense que as dúas solucións da ecuación son
A solución positiva é o valor do número áureo.
Historia do número áureo[editar | editar a fonte]
Idade antiga[editar | editar a fonte]
Existen varios textos que suxiren que o número áureo atópase como proporción nalgunhas estelas Babilonias e Asirias de arredor de 2000 a. C. Porén, non existe documentación histórica que indique que o número áureo foi usado conscientemente polos arquitectos ou artistas na construción das estelas. Tamén é importante notar que cando se mide unha estrutura complicada é fácil obter resultados curiosos se se teñen moitas medidas dispoñibles. Ademais para que se poida considerar que o número áureo está presente, as medidas deben tomarse desde puntos relativamente obvios do obxecto e este non é o caso dos elaborados teoremas que defenden a presenza do número áureo. Por todas estas razóns Mario Livio e Alvaro Valarezo conclúen que é moi improbable que os babilonios descubriran o número áureo.[3]
O primeiro en facer un estudo formal sobre o número áureo foi Euclides (c. -300--265), quen o definiu dea seguinte maneira:
"Dise que unha liña recta está dividida no extremo e o seu proporcional cando a liña enteira é ao segmento maior como o maior é ao menor."Euclides n' Os Elementos.
Euclides demostrou tamén que este número non pode ser descrito como a razón de dous números enteiros, é dicir é irracional.
Platón (c. -428-347) viviu antes de que Euclides estudara o número áureo, porén, ás veces atribúeselle o desenvolvemento de teoremas relacionados co número áureo debido que o historiador grego Proclo escribiu:
"Eudoxo... multiplicou o número de teoremas relativos á sección aos que Platón deu orixe."Proclo en Un comentario sobre o Primeiro Libro dos Elementos de Euclides.
Aquí a miúdo interpretouse a palabra sección (τομή) como a sección áurea. Con todo, a partir do século XIX esta interpretación foi motivo de gran controversia e moitos investigadores chegaron á conclusión de que a palabra sección non tivo nada que ver co número áureo. Non obstante, Platón considerou que os números irracionais, descubertos polos pitagóricos, eran de particular importancia e a chave á física do cosmos. Esta opinión tivo unha grande influencia en moitos filósofos e matemáticos posteriores, en particular os neoplatónicos.
A pesar do discutible do seu coñecemento sobre o número áureo, Platón deuse á tarefa de estudar a orixe e a estrutura do cosmos, cousa que intentou usando os cinco sólidos platónicos, construídos e estudados por Teeteto. En particular, combinou a idea de Empédocles sobre a existencia de catro elementos básicos da materia, coa teoría atómica de Demócrito, para Platón cada un dos sólidos correspondía a unha das partículas que conformaban cada un dos elementos. Segundo Platón, a terra estaba asociada ao cubo, o lume ao tetraedro, o aire ao octaedro, a auga ao icosaedro, e finalmente o Universo como un todo, estaba asociado co dodecaedro.
Idade Moderna[editar | editar a fonte]
En 1509 o matemático e teólogo Luca Pacioli publica o seu libro De Divina Proportione (A Proporción Divina), no que expresa cinco razóns polas que considera apropiado considerar divino ao Número áureo:
- A unicidade; Pacioli compara o valor único do número áureo coa unicidade de Deus.
- O feito de que estea definido por tres segmentos de recta, Pacioli asóciao coa Trindade.
- A inconmensurabilidade; para Pacioli a inconmensurabilidade do número áureo, e a inconmensurabilidade de Deus son equivalentes.
- A Autosimilaridade asociada ao número áureo; Pacioli compáraa coa omnipresencia e invariabilidade de Deus.
- Segundo Pacioli, dea mesma maneira en que Deus deu ser ao Universo a través da quinta esencia, representada polo dodecaedro; o número áureo deu ser ao dodecaedro.
En 1525, Durero publica Instrución sobre a medida con regra e compás de figuras planas e sólidas onde describe como trazar con regra e compás a espiral baseada na sección áurea, que se coñece como “espiral de Durero”.
O astrónomo Johannes Kepler (1571-1630), desenvolveu un modelo Platónico do Sistema Solar utilizando os sólidos platónicos, e referiuse ao número áureo en termos grandiosos:
“A xeometría ten dous grandes tesouros: un é o teorema de Pitágoras; o outro, a división dunha liña entre o extremo e a súa proporcional. O primeiro podémolo comparar a unha medida de ouro; o segundo debémolo denominar unha xoia preciosa”Johannes Kepler en Mysterium Cosmographicum (O Misterio Cósmico).
O primeiro uso coñecido do adxectivo áureo, dourado, ou de ouro, para referirse a este número faino o matemático alemán Martin Ohm, irmán do célebre físico Georg Simon Ohm, na segunda edición de 1835 do seu libro Die Reine Elementar Matematik (As Matemáticas Puras Elementais). Ohm escribe nunha nota ao pé:
"Un tamén acostuma chamar a esta división dunha liña arbitraria en dous partes como estas a sección dourada."Martin Ohm en Die Reine Elementar Matematik (As Matemáticas Puras Elementais).
A pesar de que a forma de escribir suxire que o termo xa era de uso común para a data, o feito de que non o incluíra na súa primeira edición suxire que o termo puido gañar popularidade arredor de 1830.
Nos textos de matemáticas que trataban o tema, o símbolo habitual para representar o número áureo foi τ do grego τομή que significa corte ou sección. Porén, a moderna denominación Φ ó φ, efectuouna en 1900 o matemático Mark Barr na honra de Fidias xa que esta era a primeira letra do seu nome escrito en grego (Φειδίας). Esta honra concédeselle a Fidias polo máximo valor estético atribuído ás súas esculturas, propiedade que xa por entón se lle atribuía tamén ao número áureo. Mark Barr e Schooling foron responsables dos apéndices matemáticos do libro The Curves of Live, de Sir Theodore Cook.
O número áureo nas matemáticas[editar | editar a fonte]
Fórmula da relación áurea[editar | editar a fonte]
Para conseguir un número cuxa relación con outro sexa φ pódese utilizar esta fórmula:
Sendo sempre a>b, a>0 y b>0
Se por exemplo, queremos un valor áureo para 2 sendo este o segmento menor, ou sexa b, resulta que:
Ordenando:
Coa fórmula Cuadrática:
Propiedades e representacións[editar | editar a fonte]
Ángulo de ouro[editar | editar a fonte]
Propiedades alxébricas[editar | editar a fonte]
- Φ é o único número real positivo tal que:
A expresión anterior é fácil de comprobar:
- Φ posúe ademais as seguintes propiedades:
- As potencias do número áureo poden ser escritas en función dunha suma de potencias de graos inferiores do mesmo número, establecendo unha verdadeira sucesión recorrente de potencias.
O caso máis simple é: , calquera sexa n un número enteiro. Este caso é unha sucesión recorrente de orde k = 2, pois recórrese a dúas potencias anteriores.
Unha ecuación recorrente de orde k ten a forma , onde é calquera número real o complexo e k é un número natural menor ou igual a n e maior ou igual a 1. No caso anterior é , y .
Pero podemos «saltear» a potencia inmediatamente anterior e escribir:
. Aquí , , , y .
Se anulamos ás dúas potencias inmediatamente anteriores, tamén hai unha fórmula recorrente de orde 6:
En xeral:
.
En resumo: calquera potencia do número áureo pode ser considerada como o elemento dunha sucesión recorrente de ordes 2, 4, 6, 8, ..., 2k; onde k é un número natural. Na fórmula recorrente é posible que aparezan potencias negativas de , feito totalmente correcto. Ademais, unha potencia negativa de corresponde a unha potencia positiva do seu inverso, a sección áurea.
Este curioso conxunto de propiedades e o feito de que os coeficientes significativos sexan os do binomio, pareceran indicar que entre o número áureo e o número e hai un parentesco.
- O número áureo é a unidade fundamental «ε» do corpo e a sección áurea é a súa inversa, «». Nesta extensión o «emblemático» número irracional cumpre as seguintes igualdades:
.
Representación mediante fraccións continuas[editar | editar a fonte]
A expresión mediante fraccións continuas é:
Esta repetición é a única onde sumar é multiplicar e restar é dividir. É tamén a máis simple de todas as fraccións continuas e a que ten a converxencia máis lenta. Esa propiedade fai que ademais o número áureo sexa un número mal aproximable mediante racionais que de feito alcanza o peor grao de aproximabilidade mediante racionais posible.[4]
Representación mediante ecuacións alxébricas[editar | editar a fonte]
O número áureo e a sección áurea son solucións das seguintes ecuacións:
Representación trigonométrica[editar | editar a fonte]
Estas corresponden ao feito de que o diámetro dun pentágono regular (distancia entre dous vértices non consecutivos) é φ veces a lonxitude do seu lado, e doutras relacións similares no pentagrama.
En 1994 deriváronse as seguintes ecuacións relacionando ao número áureo co número da Bestia:
O que pode combinarse na expresión:
Porén, hai que notar que estas ecuacións dependen de que se elixan os graos sexaxesimales como unidade angular, xa que as ecuacións non se manteñen para unidades diferentes.
Representación mediante raíces aniñadas[editar | editar a fonte]
Esta fórmula como caso particular dunha identidade xeral publicada por Nathan Altshiller-Court, da Universidade de Oklahoma, na revista American Mathematical Monthly, 1917.
O teorema xeral di:
A expresión (onde ), é igual á maior das raíces da ecuación x² - x - a = 0; ou sexa,
Relación coa serie de Fibonacci[editar | editar a fonte]
Se se denota o enésimo número de Fibonacci como Fn, e ao seguinte número de Fibonacci, como Fn + 1, descubrimos que a medida que n aumenta, esta razón oscila sendo alternativamente menor e maior que a razón áurea. Podemos tamén notar que a fracción continua que describe ao número áureo produce sempre números de Fibonacci a medida que aumenta o número duns na fracción. Por exemplo: ; ; e , o que se acerca considerablemente ao número áureo. Entón tense que:
Esta propiedade foi descuberta polo astrónomo alemán Johannes Kepler, nambergantes, pasaron máis de cen anos antes de que fora demostrada polo matemático inglés Robert Simson.
A mediados do século XIX o matemático francés Jacques Philippe Marie Binet redescubríu unha fórmula que aparentemente xa era coñecida por Leonhard Euler, e por outro matemático francés, Abraham de Moivre. A fórmula permite encontrar o enésimo número de Fibonacci sen a necesidade de producir todos os números anteriores. A fórmula de Binet depende exclusivamente do número áureo:
O número áureo na xeometría[editar | editar a fonte]
O número áureo e a sección áurea están presentes en todos os obxectos xeométricos regulares ou semiregulares nos que haxa simetría pentagonal, pentágonos ou apareza dalgunha maneira a raíz cadrada de cinco.
- Relacións entre as partes do pentágono.
- Relacións entre as partes do pentágono estrelado, pentáculo ou pentagrama.
- Relacións entre as partes do decágono.
- Relacións entre as partes do dodecaedro e do icosaedro.
O rectángulo áureo de Euclides[editar | editar a fonte]

O rectángulo AEFD é áureo porque os seus lados AE e AD están na proporción do número áureo. Euclides na súa proposición 2.11 de Os elementos obtén a súa construción.>
Con centro en G obtense o punto E, e polo tanto
resultando evidente que
de onde, finalmente
Por outra parte, os rectángulos AEFD e BEFC son semellantes, de modo que este último é así mesmo un rectángulo áureo.
No pentagrama[editar | editar a fonte]

O número áureo ten un papel moi importante nos pentágonos regulares e nos pentagramas. Cada intersección de partes dun segmento, interseca a outro segmento nunha razón áurea.
O pentagrama inclúe dez triángulos isóceles: cinco acutángulos e cinco obtusángulos. En ambos, a razón de lado maior e o menor é φ. Estes triángulos coñécense como os triángulos áureos.
Tendo en conta a gran simetría deste símbolo obsérvase que dentro do pentágono interior é posible debuxar unha nova estrela, cunha recursividade ata o infinito. Do mesmo modo, é posible debuxar un pentágono polo exterior, que sería á súa vez o pentágono interior dunha estrela máis grande. Ao medir a lonxitude total dunha das cinco liñas do pentáculo interior, resulta igual á lonxitude de calquera dos brazos da estrela maior, ou sexa Φ. Polo tanto o número de veces en que aparece o número áureo no pentagrama é infinito ao aniñar infinitos pentagramas.
O teorema de Tolomeo e o pentágono[editar | editar a fonte]

Claudio Tolomeo desenvolveu un teorema coñecido como o teorema de Tolomeo, o cal permite trazar un pentágono regular mediante regra e compás. Aplicando este teorema un cuadrilátero é formado ao quitar un dos vértices do pentágono, Se as diagonais e a base maior miden b, e os lados e a base menor miden a, resulta que b2 = a2 + ab o que implica:
Relación cos sólidos platónicos[editar | editar a fonte]
O número áureo está relacionado cos sólidos platónicos, en particular co icosaedro e o dodecaedro, cuxas dimensións están dadas en termos do número áureo. Os 12 vértices dun icosaedro con arestas de lonxitude 2, poden darse en coordenadas cartesianas polos seguintes puntos: (0, ±1, ±φ), (±1, ±φ, 0), (±φ, 0, ±1)
Os 20 vértices dun dodecaedro con arestas de lonxitude 2/φ=√5−1, tamén se poden dar en termos similares: (±1, ±1, ±1), (0, ±1/φ, ±φ), (±1/φ, ±φ, 0), (±φ, 0, ±1/φ)

Para un dodecaedro con arestas de lonxitude a, o seu volume e a súa área total pódense expresar tamén en termos do número áureo:
Se tres rectángulos áureos se solapan paralelamente nos seus centros, as 12 esquinas dos rectángulos áureos coinciden exactamente cos vértices dun icosaedro, e cos centros das caras dun dodecaedro:
O punto que os rectángulos teñen en común é o centro tanto do dodecaedro como do icosaedro.
O número áureo na natureza[editar | editar a fonte]

Na natureza, hai moitos elementos relacionados coa sección áurea e/ou os números de Fibonacci:
- Leonardo de Pisa (Fibonacci), no seu Libro dos ábacos (Liber abacci, 1202, 1228), usa a sucesión que leva o seu nome para calcular o número de pares de coellos n meses despois de que unha primeira parella comeza a reproducirse supoñendo que os coellos están illados e que empezan a reproducirse cando teñen dous meses de idade, tardan un mes desde a fecundación ata a aparición e cada camada é de dous coellos. O cociente de dous termos sucesivos da sucesión de Fibonacci tende á sección áurea ou ao número áureo se a fracción resultante é propia ou impropia, respectivamente. O mesmo sucede con toda sucesión recorrente de orde dous, segundo demostraron Barr e Schooling na revista The Field do 14 de decembro de 1912.[5]
- A disposición dos pétalos das flores (o papel do número áureo na botánica recibe o nome de Ley de Ludwig).
- A distribución das follas nun talo, que se distribúen formando ángulos de 137,5º (cociente entre 360º e o cadrado de Φ).[1] Outras relacións entre o número áureo e a filotaxe foron estudadas por Karl Schimper (1803-1867) e Auguste Bravais (1811-1863).
- A relación entre a distancia entre as espiras do interior espiralado de calquera caracol ou de cefalópodos como o nautilus. Hai polo menos tres espirais logarítmicas máis ou menos asimilables a proporcións aúreas. A primeira delas caracterízase pola relación constante igual ao número áureo entre os raio vectores de puntos situados en dous evolutas consecutivas nunha mesma dirección e sentido. As conchas do Fusus antiquus, do Murex, de Scalaria pretiosa, de Facelaria e de Solarium trochleare, entre outras, seguen este tipo de espiral de crecemento.[6][7] Débese entender que en toda consideración natural, aínda que involucre ás ciencias consideradas máis matematicamente desenvolvidas, como a Física, ningunha relación ou constante que teña un número infinito de decimais pode chegar ata o límite matemático, porque nesa escala non existiría ningún obxecto físico. A partícula elemental máis diminuta que se poida imaxinar é infinitamente máis grande que un punto nunha recta. As leis observadas e descritas matematicamente nos organismos cúmprenas transgredíndoas organicamente.[8]
- Na cantidade de elementos constituíntes das espirais ou dobres espirais das inflorescencias, como no caso do xirasol, e noutros obxectos orgánicos como as piñas dos pinos atópanse números pertencentes á sucesión de Fibonacci.
- Dise tradicionalmente que moitas relacións entre lonxitudes no corpo humano se achegan ao valor de Φ. Porén, isto só ocorre no modelo de beleza da Grecia clásica.[1]
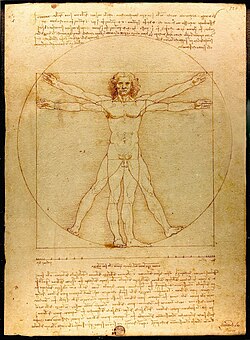
O número áureo na arte[editar | editar a fonte]
- Relacións na forma da Gran Pirámide de Gizeh. Afírmase tradicionalmente[9] que o cadrado da altura é igual á superficie dunha cara. Isto resulta teoricamente con sentido, aínda que unha construción de semellante tamaño debe conter erros inevitables a toda obra arquitectónica. Ademais, a pirámide perdeu na actualidade o revestimento.
- A relación entre as partes, o teito e as columnas do Partenón en Atenas achégase a un rectángulo áureo, aínda que as medidas exactas non se corresponden.[1]
- No cadro Leda atómica de Salvador Dalí, feito en colaboración co matemático romanés Matila Ghyka.
- O número áureo aparece nas relacións entre altura e ancho dos obxectos e persoas que aparecen nas obras de Miguel Anxo, Durero e Leonardo da Vinci, entre outros.
- A altura total do home de Vitruvio de Leonardo da Vinci é a altura do embigo multiplicada polo número áureo.
- Na novela de Dan Brown O código Da Vinci aparece unha versión desordenada dos primeiros oito números de Fibonacci (13, 3, 2, 21, 1, 1, 8, 5). Funcionan como unha pista deixada polo curador do museo do Louvre, Jacques Saunière.
- No episodio “Sabotage” da serie de televisión NUMB3RS (primeira temporada, 2005), o xenio da matemática Charlie Eppes menciona que o número fi se atopa na estrutura dos cristais, na espiral das galaxias e na cuncha do nautilus.
- Na cinta de Darren Aronofsky Pi, fe no caos o personaxe central, Max Cohen, explica a relación entre os números de Fibonacci e a sección áurea, aínda que denominándoa incorrectamente como Theta (θ) en vez de Phi (Φ).
- O número áureo aparece na película de Disney Donald in Mathmagic Land.
O número áureo no misticismo[editar | editar a fonte]
Na cruz latina, símbolo do catolicismo, a relación entre o pau vertical e o horizontal é o número áureo. Así mesmo, o pau horizontal divide a vertical en seccións áureas.[Cómpre referencia]
Notas[editar | editar a fonte]
- ↑ 1,0 1,1 1,2 1,3 Corbalán, Fernando (2010). RBA Coleccionables S. A., ed. La proporción áurea. ISBN 9788447366231.
- ↑ Este número é irracional, aínda que é alxébrico e tamén construíble mediante regra e compás, e existen numerosas racionais con maior ou menor erro. No ano 2008 obtivéronse cen mil millóns de cifras decimais correctas. (Ver: http://numbers.computation.free.fr/Constants/Miscellaneous/Records.html) Ao igual que ocorre coa raíz cadrada de dous, é posible construír un segmento idealmente exacto con regra non graduada dun so borde e lonxitude indefinida e un compás de abertura variable. Isto significa que ningún debuxo pode ser tan fino como para representar o concreto e real valor puntual do número áureo. Calquera obxecto construído polo ser humano ou formado naturalmente, aínda que se tivera a intención manifesta de lograr una representación de ese número, levaría consigo un erro inevitable. Un segmento de recta tan pequeno como o diámetro aparente da partícula atómica máis pequena ten tantos puntos xeométricos como toda a recta. Con todo, a construción xeométrica é idealmente exacta e por este motivo estimouse durante un tempo considerable á xeometría como superior á aritmética. A diferencia está en que o valor aritmético está dado como un infinito potencial e o valor xeométrico como un infinito actual, xerando un segmento de recta construíble
- ↑ Mario Livio (2002). The Golden Ratio. Broadway Books. ISBN 0-7679-0816-3.
- ↑ Bad approximable numbers in WolframMathWorld
- ↑ N. N. Vorobiov; tradución de Carlos vega (1974). Números de Fibonacci. Editorial Mir, Moscú, rústica, 112 páxinas.
- ↑ Matila Ghyka (1953). Estética das Proporcións na Naturaleza e nas Artes. Editorial Poseidón, Buenos Aires, Capítulo V: "Do Crecemento Armonioso", páxinas 118 a 144.
- ↑ D'Arcy Wentworth Thompson (1917). "On Growth and Form". Cambridge University Press. D'Arcy Wentworth Thompson (1992). "On Growth and Form". Dover edition, 1116 páxinas. D'Arcy Thompson (1980). "Sobre o Crecemento e a Forma. Editorial Hermann Blume, Madrid.Existen edicións dunhas 300 páxinas, unha recente de Cambridge.
- ↑ É unha paráfrase dun pensamento de Ruskin mencionado na páxina 139 do libro citado de Matila Ghyka
- ↑ Heródoto, Historiae, libro II, cap. 124
Véxase tamén[editar | editar a fonte]
| Wikimedia Commons ten máis contidos multimedia na categoría: Número áureo |
Bibliografía[editar | editar a fonte]
- Jarolimek (Viena, 1890). Der Mathematischen Schlüssel zu der Pyramide des Cheops.
- Kleppisch, K. (1921). Die Cheops-Pyramide: Ein Denkmal Mathematischer Erkenntnis. Múnich: Oldenburg.
- Cook, Theodore Andrea (1979; obra original: 1914). The Curves of Live. Nueva York: Dover. ISBN 0-486-23701-X; ISBN 978-0-486-23701-5.
- Pacioli, Luca (1991). La Divina Proporción. Tres Cantos: Ediciones Akal, S. A. ISBN 978-84-7600-787-7.
- Ghyka, Matila (1992). El Número de Oro. Barcelona: Poseidón, S.L. ISBN 978-84-85083-11-4.
- Ghyka, Matila (2006). El Número de Oro. I Los ritmos. II Los Ritos. Madrid: Ediciones Apóstrofe, S. L. ISBN 978-84-455-0275-4.
- Corbalán, Fernando (2010). La proporción áurea. El lenguaje matemático de la belleza. El mundo es matemático. RBA Coleccionables S. A. ISBN 978-84-473-6623-1.
- Arakelian, Hrant (2014). Mathematics and History of the Golden Section, Logos ISBN 978-5-98704-663-0 (rus.).
Outros artigos[editar | editar a fonte]
- Número π
- Espiral logarítmica
- Estrela máxica
- Sucesión de Fibonacci
- Composición áurea
- Pitágoras
- Luca Pacioli
- Matila Ghyka
- Roger Penrose
- Decágono regular
Ligazóns externas[editar | editar a fonte]
- Astronomy.swin.edu.au (Fi, a sección áurea).
- ChampionTrees.org (Fi: a proporción divina).
- GoldenRatio.com.ar (propiedades do número áureo e aplicación na bioloxía).
- MCS.Surrey.ac.uk Arquivado 05 de decembro de 2006 en Wayback Machine. (A sección áurea: fi).
- MathWorld.Wolfram.com/GoldenRatio.html (A sección áurea).
- Rt000z8y.EresMas.net (Φ en detalle]
- Rt000z8y.EresMas.net (Exemplos de Φ na vida).
- Castor.es (O número Fi na arquitectura, pintura, animais, plantas etc.)
- Gráficas de sucesións áureas en MATLAB Arquivado 21 de xuño de 2009 en Wayback Machine.
- Gráficas de sucesións áureas en MATLAB II Arquivado 21 de xuño de 2009 en Wayback Machine.
- El número de Oro - La Razón AureaArquivado 11 de maio de 2010 en Wayback Machine.
- http://www.palermo.edu/ingenieria/downloads/Investigacion/ElNumeroyloSagrado1P.pdf
































![{\displaystyle \Phi ^{n}=\sum _{i=0}^{\textstyle {\frac {1}{2}}k}{\textstyle {\frac {1}{2}}k \choose i}\Phi ^{\left[\textstyle n-\left(\textstyle {\frac {1}{2}}k+i\right)\right]}\textstyle ;k=2j\in \mathbb {N} \,\textstyle ,n\in \mathbb {R} \,\textstyle ,i\in \mathbb {N} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/a27ab6bfd4003e3beb82bdfc327a56f60564bdcc)


























![{\displaystyle F_{n}={\frac {1}{\sqrt {5}}}\left[\left({\frac {1+{\sqrt {5}}}{2}}\right)^{n}-\left({\frac {1-{\sqrt {5}}}{2}}\right)^{n}\right]\quad ={\frac {1}{\sqrt {5}}}\left[\left(\phi \right)^{n}-\left({\frac {-1}{\phi }}\right)^{n}\right]\quad }](https://wikimedia.org/api/rest_v1/media/math/render/svg/534f86233a4cc6d59d362aa34248d439937e272d)






