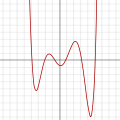Polinomio
Un polinomio é unha expresión matemática formada por indeterminados (tamén chamados variables) e coeficientes, que implica só as operacións de suma, resta, multiplicación e potencias enteiras positivas das variables. Un exemplo de polinomio dun único x indeterminado é x2 − 4x + 7. Un exemplo con tres variables é x3 + 2xyz2 − yz + 1.
Etimoloxía
[editar | editar a fonte]A palabra polinomio une dúas raíces diversas: o grego poly, que significa "moitos", e o latín nomen, ou "nome". A palabra polinomio utilizouse por primeira vez no século XVII.
Notación e terminoloxía
[editar | editar a fonte]
Un polinomio P na variable x denótase comunmente P ou P(x). Cando non é necesario salientar o nome da variable, moitas fórmulas son moito máis sinxelas e de fácil lectura se non aparecen os nomes das variables.
Podemos escribir P(a) para asignar o valor a para a variable x. Ese valor a pode pertencer a calquera dominio onde se definan a suma e a multiplicación (é dicir, calquera anel). En particular, se a é un polinomio, entón P(a) tamén é un polinomio.
Definición
[editar | editar a fonte]Unha expresión polinómica é unha expresión que se pode construír a partir de constantes e símbolos chamados variables ou indeterminados mediante a suma, a multiplicación e a exponenciación a unha potencia enteira non negativa. Normalmente as constantes son números, pero poden ser calquera expresión que non involucre os indeterminados e representen obxectos matemáticos que se poden sumar e multiplicar. Considérase que dúas expresións polinómicas definen o mesmo polinomio se se poden transformar, unha a outra, aplicando as propiedades habituais de conmutividade, asociatividade e distributividade de suma e multiplicación. Por exemplo e son dúas expresións polinómicas que representan o mesmo polinomio; así, un ten a igualdade .
Un polinomio nunha única x indeterminada sempre a pordemos reescribir na formaonde son constantes que se denominan coeficientes do polinomio, e é o indeterminado.[1] Calquera valor pode ser substituído por . A correspondencia que asocia o resultado desta substitución ao valor substituído é unha función, chamada función polinómica.
Isto pódese expresar de forma máis concisa usando a notación de suma:
Clasificación
[editar | editar a fonte]O expoñente dun indeterminado nun termo chámase grao dese indeterminado nese termo; se hai varios indeterminados o grao do termo é a suma dos graos dos indeterminados nese termo, e o grao dun polinomio é o maior grao de calquera termo con coeficiente distinto de cero.[2] Dado que x = x1, o grao dun indeterminado sen expoñente é un.
Un termo sen indeterminados e un polinomio sen indeterminados chámanse, respectivamente, termo constante e polinomio constante. O grao dun termo constante e dun polinomio constante distinto de cero é 0.
Por exemplo: é un termo con coeficiente -5, indeterminados x e y, o grao de x é 2 e o grao de y é 1, por tanto o grao do termo é 3.
Outro exemplo: consta de tres termos: o primeiro é o grao dous, o segundo é o grao un e o terceiro é o grao cero.
Aos polinomios de pequeno grao déronselles nomes específicos. Un polinomio de grao cero é un polinomio constante, ou simplemente unha constante. Os polinomios de grao un, dous ou tres son respectivamente polinomios lineares, polinomios cadráticos e polinomios cúbicos.[2]
No caso de polinomios en máis dun indeterminado, un polinomio denomínase homoxéneo de grao n se todos os seus termos distintos de cero teñen grao n. Por exemplo, x3y2 + 7x2y3 − 3x5 é homoxéneo de grao 5.
A lei conmutativa da suma pódese usar para reorganizar os termos en calquera orde preferida.
Dous termos cos mesmos indeterminados elevados ás mesmas potencias pódense sumar mediante a lei distributiva, nun único termo cuxo coeficiente é a suma dos coeficientes dos termos sumados. Os polinomios pódense clasificar polo número de termos con coeficientes distintos de cero, de xeito que un polinomio dun termo chámase monomio,[a] un polinomio de dous termos chámase binomio e un polinomio de tres termos chámase un trinomio.
Un polinomio real é un polinomio con coeficientes reais. Do mesmo xeito, un polinomio enteiro é un polinomio con coeficientes enteiros, e un polinomio complexo é un polinomio con coeficientes complexos .
Un polinomio nun indeterminado chámase polinomio univariado, un polinomio en máis dun indeterminado chámase polinomio multivariado. Un polinomio con dous indeterminados chámase polinomio bivariado.[1]
Operacións
[editar | editar a fonte]Suma e resta
[editar | editar a fonte]Os polinomios pódense sumar usando a lei asociativa da suma e reordenando usando a lei conmutativa. [3][4] Por exemplo, se temos Daquela a suma pódese reordenar e reagrupar como E simplificarse finalmente a
Cando se suman polinomios, o resultado é outro polinomio.
A resta faise de modo similar.
Multiplicación
[editar | editar a fonte]Os polinomios tamén se poden multiplicar. Cada termo dun polinomio multiplícase por cada termo do outro.[5] Por exemplo, se temos
daquela operando temosA combinación de termos similares produce
que se pode simplificar a
O produto de polinomios é sempre un polinomio.[6]
Composición
[editar | editar a fonte]Dado un polinomio dunha soa variable e outro polinomio g de calquera número de variables, a composición obtense substituíndo cada copia da variable do primeiro polinomio polo segundo polinomio. [6] Por exemplo, se e entónA composición de dous polinomios é outro polinomio.[7]
División
[editar | editar a fonte]Normalemtne a división dun polinomio por outro non é un polinomio. Estas divisións son unha familia máis xeral de obxectos, chamadas fraccións racionais, expresións racionais ou funcións racionais, dependendo do contexto. [8] Isto é análogo ao feito de que a división de dous enteiros é un número racional, non necesariamente un enteiro.[9][10]Por exemplo, a fracción 1/(x2 + 1) non é un polinomio e non se pode escribir como unha suma finita de potencias da variable x.
Con polinomios dunha variable podemos realizar a división de Euclides de polinomios, xeneralizando a división de Euclides de números enteiros. [b] Esta noción da división a(x)/b(x) dá como resultado dous polinomios, un cociente q(x) e un resto r(x), tal que a = b q + r e grao(r) < grao(b). O cociente e o resto pódense calcular mediante calquera dos varios algoritmos, incluíndo a división polinómica longa e a división sintética.[11]
Cando o denominador b(x) é mónico e tamén linear, é dicir, b(x) = x − c para algunha constante c, entón o teorema do resto polinómico afirma que o resto da división de a(x) por b(x) é a avaliación a(c). [10] Neste caso, o cociente pódese calcular mediante a regra de Ruffini, un caso especial de división sintética.[12]
Factorización
[editar | editar a fonte]Todos os polinomios con coeficientes nun dominio de factorización único (por exemplo, os números enteiros ou un corpo) tamén teñen unha forma factorizada na que o polinomio se escribe como un produto de polinomios irredutibles e unha constante. Por exemplo, a forma factorizada deé, no corpo dos enteiros e os reaise nos complexos
Cálculo
[editar | editar a fonte]Calcular derivadas e integrais de polinomios é particularmente sinxelo, en comparación con outros tipos de funcións. A derivada do polinomio con respecto a x é o polinomio Do mesmo xeito, a integral ou antiderivada xeral de é onde c é unha constante arbitraria. Por exemplo, a integral de x2 + 1 ten a forma 1/3x3 + x + c.
Para polinomios cuxos coeficientes proveñen de configuracións máis abstractas (por exemplo, se os coeficientes son números enteiros módulo algún número primo p, ou elementos dun anel), a fórmula da derivada aínda se pode interpretar formalmente, entendendo que o coeficiente kak significa a suma de k copias de ak. Por exemplo, sobre os números enteiros módulo p, a derivada do polinomio xp + x é o polinomio constante 1.[13]
Funcións polinómicas
[editar | editar a fonte]Unha función polinómica é unha función que se pode definir avaliando un polinomio.
Toda función polinómica é continua, suave e enteira.
A avaliación dun polinomio é o cálculo da función polinómica correspondente; é dicir, a avaliación consiste en substituír un valor numérico en cada indeterminado e realizar as multiplicacións e sumas indicadas.
Gráficos
[editar | editar a fonte]-
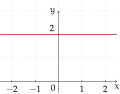
Polinomios de grao 0:
f(x) = 2 -
Polinomio de grao 1:
f(x) = 2x + 1 -
Polinomios de grao 2:
f(x) = x2 − x − 2
= (x + 1)(x − 2) -
Polinomios de grao 3:
f(x) = x3/4 + 3x2/4 − 3x/2 − 2= 1/4 (x + 4)(x + 1)(x − 2) -
Polinomios de grao 4:
f(x) = 1/14 (x + 4)(x + 1)(x − 1)(x − 3)
+ 0.5 -
Polinomios de grao 5:
f(x) = 1/20 (x + 4)(x + 2)(x + 1)(x − 1)
(x − 3) + 2 -
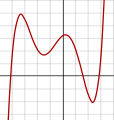
Polinomios de grao 6:
f(x) = 1/100 (x6 − 2x 5 − 26x4 + 28x3+ 145x2 − 26x − 80) -
Polinomios de grao 7:
f(x) = (x − 3)(x − 2)(x − 1)(x)(x + 1)(x + 2)(x + 3)
Unha función polinómica non constante tende ao infinito cando a variable aumenta indefinidamente (en valor absoluto). Se o grao é superior a un, a gráfica non ten asíntota ningunha, nese caso ten dúas ramas parabólicas con dirección vertical (unha rama para x positivo e outra para x negativo).
Ecuacións
[editar | editar a fonte]Unha ecuación polinómica, tamén chamada ecuación alxébrica, é unha ecuación da forma [14]Por exemplo,Unha ecuación polinómica contrasta cunha identidade polinómica como (x + y)(x − y) = x2 − y2, onde ambas as expresións representan o mesmo polinomio en diferentes formas e, como consecuencia, calquera avaliación de ambos os membros dá unha igualdade válida.
En álxebra elemental, ensínanse métodos como a fórmula cadrática para resolver todas as ecuacións polinómicas de primeiro e segundo grao nunha soa variable. Tamén pódense usar algoritmos de busca de raíces para atopar aproximacións numéricas das raíces dunha expresión polinómica de calquera grao.
O número de solucións dunha ecuación polinómica con coeficientes reais non pode exceder o grao, e é igual ao grao cando as solucións complexas se contan coa súa multiplicidade. Este feito chámase teorema fundamental da álxebra.
Un número a é unha raíz dun polinomio P se e só se o polinomio linear x − a divide P, é dicir, se existe outro polinomio Q tal que P = (x − a) Q. Pode ocorrer que unha potencia (maior que 1) de x − a divida P ; neste caso, a é unha raíz múltiple de P, e se non a é unha raíz simple de P. Se P é un polinomio distinto de cero, existe a maior potencia m tal que (x − a)m divide P, que se chama multiplicidade de a como raíz de P. O número de raíces dun polinomio P distinto de cero, contado coas súas respectivas multiplicidades, non pode exceder o grao de P,[15] e é igual a este grao se se consideran todas as raíces complexas (isto é unha consecuencia do teorema fundamental da álxebra). Os coeficientes dun polinomio e as súas raíces están relacionados mediante as fórmulas de Viète.
En 1824, Niels Henrik Abel demostrou o resultado de que hai ecuacións de grao 5 cuxas solucións non se poden expresar mediante unha fórmula (finita), que só implican operacións aritméticas e radicais (ver teorema de Abel-Ruffini). En 1830, Évariste Galois demostrou que a maioría das ecuacións de grao superior a catro non se poden resolver mediante radicais, e demostrou que para cada ecuación pódese decidir se é resoluble por radicais e, se é así, resolvela. Este resultado marcou o inicio da teoría de Galois e da teoría de grupos, dúas ramas importantes da álxebra moderna.
Cando non hai unha expresión alxébrica para as raíces, e cando tal expresión alxébrica existe mais é demasiado complicada para ser útil, a única forma de resolvela é calcular aproximacións numéricas das solucións.[16] (Ver Algoritmo de busca de raíces).
Para polinomios con máis dun indeterminado, as combinacións de valores das variables para as que a función polinómica toma o valor cero chámanse xeralmente ceros en lugar de "raíces". (Ver Sistema de ecuacións polinómicas).
O caso especial no que todos os polinomios son de grao un chámase sistema de ecuacións lineares, para o cal existe outra gama de métodos de solución diferentes, incluíndo a eliminación clásica de Gauss.
Unha ecuación polinómica na que só se queren as solucións que son enteiros chámase ecuación diofantiana. Resolver ecuacións diofantianas é xeralmente unha tarefa moi difícil. Probouse que non pode haber ningún algoritmo xeral para resolvelas, nin sequera para decidir se o conxunto de solucións está baleiro (ver o décimo problema de Hilbert). Algúns dos problemas máis famosos que se resolveron durante os últimos cincuenta anos están relacionados coas ecuacións diofántianas, como o último teorema de Fermat.
Notas
[editar | editar a fonte]- ↑ 1,0 1,1 Weisstein, Eric W. "Polynomial". mathworld.wolfram.com (en inglés). Consultado o 2020-08-28.
- ↑ 2,0 2,1 "Polynomials | Brilliant Math & Science Wiki". brilliant.org (en inglés). Consultado o 2020-08-28.
- ↑ Edwards, Harold M. (1995). Linear Algebra. Springer. p. 47. ISBN 978-0-8176-3731-6.
- ↑ Salomon, David (2006). Coding for Data and Computer Communications. Springer. p. 459. ISBN 978-0-387-23804-3.
- ↑ Salomon, David (2006). Coding for Data and Computer Communications. Springer. p. 459. ISBN 978-0-387-23804-3.
- ↑ 6,0 6,1 Barbeau 2003, p. 1–2
- ↑ Kriete, Hartje (1998-05-20). Progress in Holomorphic Dynamics (en inglés). CRC Press. p. 159. ISBN 978-0-582-32388-9.
This class of endomorphisms is closed under composition,
- ↑ Marecek, Lynn; Mathis, Andrea Honeycutt (6 May 2020). Intermediate Algebra 2e. OpenStax. §7.1.
- ↑ Haylock, Derek; Cockburn, Anne D. (2008-10-14). Understanding Mathematics for Young Children: A Guide for Foundation Stage and Lower Primary Teachers. SAGE. p. 49. ISBN 978-1-4462-0497-9.
We find that the set of integers is not closed under this operation of division.
- ↑ 10,0 10,1 Marecek & Mathis 2020
- ↑ Selby, Peter H.; Slavin, Steve (1991). Practical Algebra: A Self-Teaching Guide (2nd ed.). Wiley. ISBN 978-0-471-53012-1.
- ↑ Weisstein, Eric W. "Ruffini's Rule". mathworld.wolfram.com (en inglés). Consultado o 2020-07-25.
- ↑ Barbeau 2003, pp. =CynRMm5qTmQC&pg=PA64 64–5
- ↑ Proskuryakov, I.V. (1994). "Algebraic equation". En Hazewinkel, Michiel. Encyclopaedia of Mathematics 1. Springer. ISBN 978-1-55608-010-4.
- ↑ Leung, Kam-tim (1992). Polynomials and Equations. Hong Kong University Press. p. 134. ISBN 9789622092716.
- ↑ McNamee, J.M. (2007). Numerical Methods for Roots of Polynomials, Part 1. Elsevier. ISBN 978-0-08-048947-6.
Véxase tamén
[editar | editar a fonte]| Wikimedia Commons ten máis contidos multimedia na categoría: Polinomio |
Bibliografía
[editar | editar a fonte]- Barbeau, E.J. (2003). Polynomials. Springer. ISBN 978-0-387-40627-5.
- Bronstein, Manuel; et al., eds. (2006). Solving Polynomial Equations: Foundations, Algorithms, and Applications. Springer. ISBN 978-3-540-27357-8.
- Cahen, Paul-Jean; Chabert, Jean-Luc (1997). Integer-Valued Polynomials. American Mathematical Society. ISBN 978-0-8218-0388-2.
- Horn, Roger A.; Johnson, Charles R. (1990). Matrix Analysis. Cambridge University Press. ISBN 978-0-521-38632-6..
- Leung, Kam-tim; et al. (1992). Polynomials and Equations. Hong Kong University Press. ISBN 9789622092716.
- Mayr, K. (1937). Über die Auflösung algebraischer Gleichungssysteme durch hypergeometrische Funktionen. Monatshefte für Mathematik und Physik 45. pp. 280–313. doi:10.1007/BF01707992.
- McCoy, Neal H. (1968). Introduction To Modern Algebra, Revised Edition. Boston: Allyn and Bacon. LCCN 68015225.
- Prasolov, Victor V. (2005). Polynomials. Springer. ISBN 978-3-642-04012-2.
- Sethuraman, B.A. (1997). "Polynomials". Rings, Fields, and Vector Spaces: An Introduction to Abstract Algebra Via Geometric Constructibility. Springer. ISBN 978-0-387-94848-5.
- Toth, Gabor (2021). "Polynomial Expressions". Elements of Mathematics. Undergraduate Texts in Mathematics. pp. 263–318. ISBN 978-3-030-75050-3. doi:10.1007/978-3-030-75051-0_6.
- Umemura, H. (2012) [1984]. "Resolution of algebraic equations by theta constants". En Mumford, David. Tata Lectures on Theta II: Jacobian theta functions and differential equations. Springer. pp. 261–. ISBN 978-0-8176-4578-6.
- Varberg, Dale E.; Purcell, Edwin J.; Rigdon, Steven E. (2007). Calculus (9th ed.). Pearson Prentice Hall. ISBN 978-0131469686.
- von Lindemann, F. (1884). Ueber die Auflösung der algebraischen Gleichungen durch transcendente Functionen. Nachrichten von der Königl. Gesellschaft der Wissenschaften und der Georg-Augusts-Universität zu Göttingen 1884. pp. 245–8.
- von Lindemann, F. (1892). Ueber die Auflösung der algebraischen Gleichungen durch transcendente Functionen. II. Nachrichten von der Königl. Gesellschaft der Wissenschaften und der Georg-Augusts-Universität zu Göttingen 1892. pp. 245–8.
Outros artigos
[editar | editar a fonte]Ligazóns externas
[editar | editar a fonte]- Markushevich, A.I. (2001) [1994]. "Polynomial". Encyclopedia of Mathematics. EMS Press.
- "Euler's Investigations on the Roots of Equations". Arquivado dende o orixinal o 22 de maio de 2011. Consultado o 13 de maio de 2024.