Derivada

A derivada é unha operación realizada ás funcións dentro do cálculo infinitesimal (ou cálculo diferencial e integral) polo cal se busca un cálculo que relacione a variación (aumento o diminución) do valor dependente da función segundo o valor da variable independente, é dicir, canto aumenta y por cada aumento de x. Para que unha función sexa derivable nun punto $x_a \,$ ten que ser continua na súa contorna pola dereita e pola esquerda e ter o mesmo límite polos dous lados. Nese caso defínese a derivada coma o resultado de:

$f' (x_a) = \lim_{h \to 0} \frac{f(x_a+h)-f(x_a)}{h} = \lim_{h \to 0} \frac{f(x_a-h)-f(x_a)}{-h} \,$

Do mesmo xeito pódese definir o valor da función derivada para calquera punto do dominio de $f(x) \,$, na cal se expresa o valor da derivada para tódolos puntos continuos do dominio:

$f'(x) = \lim_{h \to 0} \frac{f(x+h)-f(x)}{h} = \lim_{h \to 0} \frac{f(x-h)-f(x)}{-h} \,$

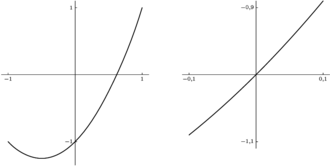
Exemplos da definición

Derivada dunha función polinómica:

$f(x) \,$	$= 3x^2 + 2x - 6 \, \Rightarrow$
$f'(x) \,$	$= \lim_{h \to 0} \frac{f(x+h) - f(x)}{h}$
	$= \lim_{h \to 0} \frac{(3(x+h)^2 + 2(x+h) - 6) - (3x^2 + 2x - 6) }{h}$
	$= \lim_{h \to 0} \frac{(3(x^2 + h^2 + 2xh) + 2(x+h) - 6) - (3x^2 + 2x - 6)}{h}$
	$= \lim_{h \to 0} \frac{(3x^2 +3h^2 + 6xh + 2x + 2h - 6) - (3x^2 + 2x - 6)}{h}$
	$= \lim_{h \to 0} \frac{3x^2 +3h^2 + 6xh + 2x + 2h - 6 - 3x^2 - 2x + 6}{h}$
	$= \lim_{h \to 0} \frac{3h^2 + 6xh + 2h}{h}$
	$= \lim_{h \to 0} 3h + 6x + 2$
	$= 6x + 2 \,$

Derivada da función logaritmo:

• $f(x) = \log_a x \,$
• $f(x+h) = \log_a (x+h) \,$
• $f(x+h) - f(x) = \log_a (x+h) - \log_a x = \log_a \frac{x+h}{x} \,$
• $\frac{f(x+h) - f(x)}{h} =$

Táboa de funcións derivadas

PROPIEDADE	PRIMITIVA	DERIVADA
Derivada dunha constante	$k \,$	$0 \,$
Derivada de x	$x \,$	$1 \,$
Derivada de k x	$k \, x \,$	$k \,$
Produto por escalares, xeralización do anterior	$k \, f(x) \,$	$k \, f'(x) \,$
Derivada dunha suma	$f(x) + g(x) \,$	$f'(x) + g'(x) \,$
Derivada dun produto	$f(x) \, g(x) \,$	$f'(x) \, g(x) + f(x) \, g'(x) \,$
Derivada dunha división, deducida da do produto	$\frac{f(x)}{g(x)}$	$\frac{f'(x) g(x) - f(x) g'(x)}{g^2 (x)}$
Derivada dunha potencia, deducida da do produto ($x\in\mathbb{R}$)	$f(x)^m \,$	$m \, f(x)^{m-1} \, f'(x) \,$
Derivada dun logaritmo	$\log_a f(x) \,$	$\frac{1}{f(x) log_e(a)} \, f'(x)$
Derivada dunha exponencial	$a^{f(x)} \,$	$a^{f(x)} \, log_e a \, f'(x)$
Derivada trigonométrica 1	$\sin f(x) \,$	$\cos f(x) \, f'(x)$
Derivada trigonométrica 2	$\cos f(x) \,$	$-\sin f(x) \, f'(x)$
Derivada trigonométrica 3	$\tan f(x) \,$	$\sec^2 f(x) \, f'(x)$
Derivada trigonométrica 4	$\sec f(x) \,$	$\sec f(x) \, \tan f(x) \, f'(x)$
Derivada trigonométrica 5	$\mbox{cosec} \, f(x) \,$	$-\mbox{cosec} f(x) \, \mbox{cotan} f(x) \, f'(x)$
Derivada trigonométrica 6	$\mbox{cotan} \, f(x) \,$	$-\sec^2f(x) \, f'(x)$
Derivada trigonométrica inversa 1	$\mbox{arcsin} \, f(x) \,$	$\frac{ f'(x) }{\sqrt{ 1 - f^2(x) }}$
Derivada trigonométrica inversa 2	$\mbox{arccos} \, f(x) \,$	$\frac{ -f'(x) }{\sqrt{ 1 - f^2(x) }}$
Derivada trigonométrica inversa 3	$\mbox{arctan} \, f(x) \,$	$\frac{ f'(x) }{ 1 + f^2(x) }$
Derivada trigonométrica inversa 4	$\mbox{arcsec} \, f(x) \,$	$\frac{ -f'(x) }{ 1 + f^2(x) }$
Derivada trigonométrica inversa 5	$\mbox{arccosec} \, f(x) \,$	$\frac{ f'(x) }{f(x) \sqrt{ f^2(x) - 1}} = \frac{ f'(x) }{\sqrt{ f^4(x) - f^2(x) }}$
Derivada trigonométrica inversa 6	$\mbox{arccotan} \, f(x) \,$	$\frac{ -f'(x) }{f(x) \sqrt{ f^2(x) - 1}} = \frac{ -f'(x) }{\sqrt{ f^4(x) - f^2(x) }}$

Exemplos de aplicación

lim 2x+1= x->2

Utilidade

O uso da derivación ten valido para explicar ou determinar multitude de situacións da física ou da xeometría. Un pequeno exemplo pode ser a seguinte táboa:

FIGURA	LONXITUDE	SUPERFICIE	VOLUME
Círculo & circunferencia	(Circunferencia) $2 \pi r \,$	(Círculo) $\pi r^2 \,$	NON PROCEDE
Esfera	NON PROCEDE	$4 \pi r^2 \,$	$\frac{4}{3} \pi r^3 \,$

onde se pode comprobar que o valor de dimensión espacial N se corresponde coa derivada do valor de dimensión espacial N+1 da mesma figura.

Outro caso na física sería o valor da posición, velocidade e aceleración dunha partícula expresadas en función do tempo, que son cada unha derivada da anterior:

$\begin{matrix} \mbox{posición} & p = & p_0 + & v_0 t + & \frac{1}{2} a_0 t^2 \\ \mbox{velocidade} & v= & & v_0 + & a_0 t \\ \mbox{aceleración} & a= & & & a_0 \end{matrix}$

Véxase tamén

Outros artigos

• Diferencial
• Integración
• Cálculo integral
• Lista de integrais