Función trigonométrica
En Matemáticas, as funcións trigonométricas son funcións dun argumento angular, importantes en diversas aplicacións, derivadas do estudo da xeometría dos triángulos e fundamentais no estudo dos fenómenos periódicos.
Poden ser definidas como razóns (cocientes) de dous lados dun triángulo rectángulo contendo o ángulo argumento, ou, máis xeralmente, como cocientes de coordenadas de puntos que definen un círculo de raio unidade, ou, de xeito aínda máis xenérico, como sumatorio de series infinitas ou de xeito equivalente como solucións de certas ecuacións diferenciais, como é presentado máis abaixo.
Hai seis funcións trigonométricas básicas. As catro últimas están definidas en función das dúas primeiras, indicando que as catro ecuacións consignadas abaixo son definicións e non identidades probadas.
- seno (sen)
- coseno (cos)
- tanxente (tan = sen / cos)
- secante (sec = 1 / cos)
- cosecante (cosec = 1 / sen)
- cotanxente (cot = cos / sen)
Existen diversas relacións entre estas funcións, chamadas identidades trigonométricas.
Historicamente foron usadas outras funcións, pero agora son pouco empregadas.
Definicións nun triángulo rectángulo[editar | editar a fonte]

Para definir as funcións trigonométricas do ángulo A, comezamos cun triángulo rectángulo arbitrario que contén o ángulo A:
Definicións básicas:
- Hipotenusa é o ángulo oposto ó ángulo recto, notado como h.
- Lado oposto é o lado oposto ó ángulo no que estamos interesados, neste caso é designado como a (minúsculo para enfrontalo a A, o ángulo de referencia).
- Lado contiguo é o forma o ángulo coa hipotenusa, neste caso b.
Entón,
1). O seno dun ángulo é a razón entre as lonxitudes do lado oposto e da hipotenusa. No noso caso,
- sen(A) = op/hip = a/h.
A notar que esta razón non depende do triángulo escollido, senón de que conteña o ángulo A, pois todos os triángulos con esa característica teñen funcións trigonométricas do mesmo valor para dito ángulo.
2). O coseno dun ángulo é a razón entre as lonxitudes do lado contiguo e da hipotenusa. No noso caso,
- cos(A) = cont/hip = b/h.
3). A tanxente dun ángulo é a razón entre as lonxitudes do lado oposto e do lado contiguo. No noso caso,
- tan(A) = op/cont = a/b.
As outras tres funcións son definidas máis claramente usando as anteriores.
4). A cosecante cosec(A) é a inversa do sen(A), é dicir, a razón entre as lonxitudes da hipotenusa e o lado oposto:
- cosec(A) = hip/op = h/a.
5). A secante sec(A) é a inversa do cos(A), ou sexa, a razón entre as lonxitudes da hipotenusa e lado contiguo:
- sec(A) = hip/cont = h/b.
6). A cotanxente cot(A) é a inversa da tan(A), ou sexa, a razón entre as lonxitudes do lado contiguo e o lado oposto:
- cot(A) = cont/op = b/a.
Mnemotecnia[editar | editar a fonte]
Hai un certo número de regras mnemotécnicas para as definicións anteriores, por exemplo SOH CCH TOC lémbranos que:
- SOH ... sen = oposto/hipotenusa
- CCH ... cos = contiguo/hipotenusa
- TOC ... tan = oposto/contiguo.
Pódense ver máis en Regras mnemotécnicas en trigonometría.
Cálculo[editar | editar a fonte]
As funcións trigonométricas foron tabuladas para moitos valores. As calculadoras científicas están pensadas para poder tamén calcular ditas funcións usando series de Taylor (descrición abaixo) ou outro método semellante. Para algúns ángulos sinxelos, os valores correspondentes poden ser calculados de xeito sinxelo a man, como nos exemplos seguintes. O seno, coseno e tanxente de calquera múltiplo enteiro de 3º (π/60 radiáns) pode ser calculado de xeito exacto a man.
Se supoñemos que temos un triángulo rectángulo onde os dous ángulos restantes son iguais, entón son = 45º (π/4 radiáns), e polo tanto, as lonxitudes do lado b e a do a son iguais; podemos coller a =b= 1. Agora, podemos determinar seno, coseno e tanxente de dito ángulo de π/4 radiáns. Usando o Teorema de Pitágoras, c = √(a2 + b2) = √2, como ilustra a figura:

Polo tanto,
Para determinar as funcións trigonométricas para ángulos de 60º (π/3 radiáns) e 30º (π/6 radiáns), comezamos cun triángulo equilátero de lonxitude de lado igual a 1. Todos os seus ángulos son de 60º. Ó dividilo noutros dous simétricos, obtemos un triángulo rectángulo con ángulos de 30º e 60º. Para un triángulo tal, o lado menor = 1/2, e o maior (excepto a hipotenusa, que mide 1), =(√3)/2. Polo tanto

e
Definicións sobre a circunferencia unitaria[editar | editar a fonte]
Os seis funcións trigonométricas poden ser definidas tamén en termos da circunferencia unidade, a circunferencia de raio=1 centrada na orixe. A definición permite un cálculo doado e práctico, a partir da consideración de que un punto calquera dela pode darnos un triángulo rectángulo contando co centro (0,0) e os eixes coordenados. Asemade permite unha visualización do xa visto.
A ecuación para a circunferencia unidade é:
e a visualización, con indicacións:

No debuxo, son dados algúns ángulos máis comúns (expresados en radiáns). Nótese que os ángulos están expresados como positivos seguindo o movemento contrario ás agullas do reloxo e os negativos, en sentido contrario. Cando unha liña fai un ángulo θ coa metade positiva do eixe x intersecta a circunferencia unidade. As coordenadas x e y deste punto de intersección son iguais ó cos θ e sen θ, respectivamente. O triángulo no gráfico revela a razón: O raio é igual á hipotenusa e ten lonxitude 1, polo que temos sen θ = y/1 e cos θ = x/1. A circunferencia unitaria pode ser vista como un xeito de obter un número infinito de triángulos que varían as lonxitudes dos seus lados pero non a da súa hipotenusa, constantemente igual a 1.
Para ángulos maiores que 2π ou menores que −2π, sinxelamente continúase a rotar arredor da circunferencia. Neste senso, seno e coseno vólvense funcións periódicas de período 2π:
para calquera ángulo θ e calquera enteiro k.
O máis pequeno período positivo dunha función periódica chámase período primitivo da función. O Período primitivo do seno, coseno, secante ou cosecante é un círculo completo, i.e. 2π radiáns ou 360 graos; o da tanxente ou cotanxente é só un semicírculo, i.e. π radiáns ou 180 graos.
Arriba, só o seno e coseno foron definidos directamente sobre a circunferencia unidade, mais as outras catro funcións elementais en trigonometría poden ser definidas por:

De xeito alternativo, todas as funcións trigonométricas básicas poden ser definidas sobre a circunferencia unidade, do xeito usado historicamente. En particular, para unha corda do círculo, onde θ é a metade do ángulo subtendido, sen(θ) é GF (a metade da corda), definición introducida na India (como pode verse abaixo). cos(θ) é a distancia horizontal OG, tan(θ) é a lonxitude do segmento FE da liña tanxente á circunferencia en F, de aquí o nome tanxente para esta función. cot(θ) é outro segmento tanxente, DF. sec(θ) = OE e cosec(θ) = OD son segmentos de liñas secantes (intersecando a circunferencia en dous puntos), e poden ser vistos como proxeccións de OF ó longo da tanxente en F nos eixes horizontal e vertical, respectivamente. A partir desta construción, é doado ver que secante e tanxente diverxen cando θ se aproxima a π/2 (90º) e que cosecante e cotanxente fáno cando θ se aproxima a cero.
Preséntase aquí un gráfico de seno e coseno:

Definicións por series[editar | editar a fonte]

Advertencia: Aquí, e en xeral no cálculo, é de importancia capital que os ángulos sexan expresados en radiáns.
Usando só xeometría e propiedades de límites, pode amosarse que a derivada do seno é o coseno, e a do coseno é menos o seno. Pode usarse entón a teoría das series de Taylor para amosar que as seguintes identidades se manteñen para todo número real x:
Estas identidades son a miúdo tomadas como definicións das funcións seno e coseno. Así, con frecuencia, son usadas como punto de partida nun tratamento rigoroso das funcións trigonométricas e as súas aplicacións (i.e. en series de Fourier), pois a teoría das series infinitas pode ser desenvolvida a partir dos fundamentos dos números reais, independentemente de calquera outra consideración xeométrica. A diferenciabilidade e continuidade destas funcións están establecidas unicamente a partir das definicións por series.
Relacións coa función exponencial[editar | editar a fonte]
Subministrando argumentos complexos ás funcións seno e coseno, amósase que teñen partes imaxinarias e reais, respectivamente, da función exponencial complexa cando o seu argumento é puramente imaxinario:
Esta relación foi notada en primeiro lugar por Euler e a identidade é chamada fórmula de Euler da análise complexa. Neste xeito, as funcións trigonométricas vólvense esenciais na interpretación xeométrica da análise complexa. Por exemplo, coa anterior identidade, se se considera que a circunferencia unidade no plano de , definida por eix, e como anteriormente, podemos parametrizar esta circunferencia en termos de senos e cosenos, a relación entre a exponencial complexa e as funcións trigonométricas vólvese máis patente.
Ademais, isto permite para a definición das funcións trigonométricas para argumentos complexos z:
O que amosa que os procesos exponenciais están intimamente ligados ó comportamento periódico.
Definicións mediante ecuacións diferenciais[editar | editar a fonte]
Tanto o seno como o coseno satisfán a ecuación diferencial
é dicir, cada unha é a inversa aditiva da súa derivada segunda. No espazo vectorial bidimensional V consistente en todas as solucións desta ecuación, a función seno é a solución única que satisfai as condicións iniciais y(0) = 0 e y′(0) = 1, e a función coseno é a única que satisfai as condicións iniciais y(0) = 1 e y′(0) = 0. Noutras palabras, as funcións seno e coseno son solucións particulares que xuntas forman a base de V. Este método de definir seno e coseno é equivalente ao da fórmula de Euler. (Ver ecuación diferencial lineal.) Esta ecuación diferencial pode ser usada non só para definir seno e coseno, senón tamén para probar as identidades trigonométricas de ditas funcións.
A función tanxente é a única solución á ecuación da ecuación diferencial non linear.
satisfacendo as condicións iniciais y(0) = 0. Esta é unha proba visual moi interesante de que a función tanxente satisfai esta ecuación diferencial.[1]
Funcións inversas[editar | editar a fonte]
As funcións trigonométricas son periódicas, polo que podemos restrinxir os seus dominios antes de definir unha única inversa. No que segue, as funcións á esquerda son definidas pola ecuación á súa dereita; non son identidades probadas. As inversas principais son definidas como:
Para as funcións trigonométricas inversas, a notación sen− 1 e cos− 1 é a miúdo substituída por arcsen e arccos etc.
Estas funcións poden ser definidas probando que son antederivadas doutras funcións. Entón, cada función está determinada de xeito único polo seu valor nun único punto:
Nota: arcsec pode ser chamado arcsegundo.
Identidades[editar | editar a fonte]
- Artigo principal: Identidade trigonométrica.
Propiedades e aplicacións[editar | editar a fonte]
As funcións trigonométricas, cono suxire o seu nome, son básicas en trigonometría, en particular a causa dos seguintes resultados:
A lei dos senos para un triángulo arbitrario establece:
O que pode probarse por división do triángulo en dous rectángulos e usando a definición anterior de seno. sen(A)/a no teorema é recíproco do diámetro do círculo a través de tres puntos A, B e C. A lei é útil para cálculo das lonxitudes dos lados descoñecidos dun triángulo se son dados dous ángulos e un lado. Esta é unha situación común en triangulación, unha técnica para determinar distancias descoñecidas a partir da medida de dous ángulos e unha distancia implicada accesible.
Se o ángulo non está contido entre dous lados, o triángulo pode non ser único.
A lei dos cosenos é unha extensión do Teorema de Pitágoras:
De novo, este teorema pode ser probado dividindo o triángulo en dous rectángulos. Esta lei é útil para determinar o dato descoñecido dun triángulo se son coñecidos dous lados e un ángulo.
Hai tamén unha lei de tanxentes:
As funcións trigonométricas son tamén importantes fora do estudo dos triángulos. Existen funcións periódicas con formatos gráficos característicos, útis para modelar fenómenos recorrentes como ondas de son ou luz. Cada sinal pode ser escrita como unha suma infinita de funcións seno e coseno de diferentes frecuencias; esa é a idea básica da análise de Fourier, no que as series trigonométricas son usadas para resolver unha variedade de problemas de ecuacións de diferenciais parciais con valores nos límites.
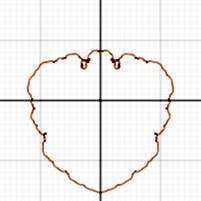
A imaxe da dereita amosa un gráfico bidimensional baseado unha suma de senos e cosenos, ilustrando o feito de que as series de Fourier poden describir curvas de complicación arbitraria. A súa ecuación é:
onde F(n) é o enésimo número de Fibonacci.
Para un cálculo de moitas relacións entre funcións trigonométricas, ver o artigo identidade trigonométrica.
Historia[editar | editar a fonte]
O estudo sistemático máis antigo das funcións trigonométricas e a tabulación dos seus valores foi levado a cabo por Hiparco de Nicea (180 a.C.-a25 a.C.), que tabulou as lonxitudes dos arcos de circunferencia (ángulo A veces o radio r) coas lonxitudes das cordas subtendidas (2r sin(A/2)). Despois, Tolomeo (S. II) ampliou dito traballo no seu Almaxesto, derivando as fórmulas de suma e resta para os equivalentes de sin(A + B) e cos(A + B). Tolomeo tamén derivou o equivalente da fórmula do ángulo metade sin(A/2)2 = (1 − cos(A))/2, permeténdolle crear táboas con calquera precisión desexada. Ningunha das táboas anteriores sobreviviu ata os nosos días.
O seguinte desenvolvemento significativo da trigonometría foi na India, nos traballos coñecidos como Siddhantas (S. IV e S. V), que definiu por vez primeira o seno como a relación moderna entre a metade dun ángulo e a metade dunha corda. Os Siddhantas tamén contiñan as táboas máis antigas de valores do seno que lograron sobrevivir ata a actualidadea, en intervalos de 3,75º, dende 0º a 90º.
Os traballos na India foron despois traducidos e mellorados polos árabes, que no século X (no traballo de Abu'l-Wefa) usaban as seis funcións trigonométricas sinxelas que coñecemos na actualidade, e tiñan táboas de senos con incrementos de 0,25º e oito cifras significativas, así como táboas de tanxentes.
O noso moderno nome de seno ven, vía sinus ("baía" ou "pregue") en latín, dunha tradución errónea do sánscrito jiva (ou jya). jiva (orixinariamente ardha-jiva, "media-corda", no S. VI Aryabhatiya) foi trasliterada polos árabes como jiba, pero confundiuse con outro nome, jaib ("baía"), polos tradutores europeos como Roberto de Chester e Xerardo de Cremona en Toledo no S. XII, pode que a causa de abreviar en árabe jiba como jb.
Todos os anteriores traballos antes citados trataban a trigonometría como unha parte adxunta no estudo da astronomía; pode que o primeiro tratamento como tema independente fora en De triangulis omnimodus (1464) de Regiomontano (1436 - 1476), así como no seu posterior Tabulae directionum (que incluía a función tanxente).
O Opus palatinum de triangulis de Reticus, un estudante dea Copérnico, foi o primeiro en definir as funcións trigonométricas directamente en termos de triángulos rectángulos en troques de círculos, con táboas para as seis funcións trigonométricas; este traballo foi finalizado por Valentin Otho, estudante de Reticus, no 1596.
O Introductio in analysin infinitorum (1748) de Euler foi responsable do establecemento do tratamento analítico das funcións trigonométricas, definíndoas como series infinitas e presentando a "Fórmula de Euler" eix = cos(x) + i sin(x). Euler usou as abreviaturas sin., cos., tang., cot., sec., e cosec..
Véxase tamén[editar | editar a fonte]
| Commons ten máis contidos multimedia sobre: Función trigonométrica |
Bibliografía[editar | editar a fonte]
- Carl B. Boyer, A History of Mathematics, 2nd ed. (Wiley, Nova York, 1991).
- Eli Maor, Trigonometric Delights (Princeton Univ. Press, 1998).
- "Trigonometric functions", MacTutor History of Mathematics Archive.
- Tristan Needham, Visual Complex Analysis, (Oxford University Press, 2000), ISBN 0-19-853446-9 Web do libro Arquivado 03 de agosto de 2004 en Wayback Machine.
Outros artigos[editar | editar a fonte]
- Xeración de táboas trigonométricas
- Función hiperbólica
- Pitágoras
- Teorema de Pitágoras
- Identidade trigonométrica
- Constantes trigonométricas exactas
Ligazóns externas[editar | editar a fonte]
- Dave's Short Trig Course usa applets de java, moi útil para o ensino das funcións trigonométricas.
- ↑ "Copia arquivada" (PDF). Arquivado dende o orixinal (PDF) o 02 de xuño de 2004. Consultado o 29 de agosto de 2004.













































![{\displaystyle {\frac {a+b}{a-b}}={\frac {\tan[{\frac {1}{2}}(A+B)]}{\tan[{\frac {1}{2}}(A-B)]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc3a9eabede6ceceb176a58754cf6557b46f7c3c)
