Triángulo

Un triángulo, en xeometría plana, é un polígono de tres lados con tres ángulos internos que suman 180º. Os vértices, onde concorren os lados, son tres puntos coplanarios non aliñados.
Tamén se pode definir un triángulo en superficies xerais, sendo diferentes as súas propiedades. Se está contido nunha superficie esférica denomínase triángulo esférico. Na cartografía, representando a superficie terrestre, denomínase triángulo xeodésico.
Notación[editar | editar a fonte]

Cómpre ter unha fórmula estándar para definir un triángulo. Aos puntos, pois tense o costume de designalos con letras latinas maiúsculas, e así, nun triángulo, os vértices son A, B e C. Daquela, con isto, un triángulo defínese empregando os seus vértices e así temos o triángulo ABC. Nótese, que por ser triángulo, dá igual a orde en que poñamos os puntos, pois vai coincidir sempre co trazado do seu perímetro, cousa que non pasa cos outros polígonos, onde para definilos ben hai que ter en conta o percorrido que fai o seu perímetro.
Os lados do triángulo anótanse, como calquera segmento, indicando os extremos: AB, BC e AC ou CA. Para designar o valor da lonxitude do segmento, xeralmente, empregamos o nome do vértice oposto, converténdoo en minúscola, e así temos para BC, para AC e para AB.
Para os ángulos, como norma xeral, empréganse os segmentos que o conforman indicando cal é o vértice, por exemplo, AB e BC, que comparten o punto B, o ángulo é Tamén se utiliza unha letra minúscula, habitualmente grega, algunhas veces cun acento circunflexo, para este labor, e nalgúns casos, pois empregase o vértice correspondente cun acento circunflexo. Seguindo o noso exemplo temos:
Propiedades dos triángulos[editar | editar a fonte]
- A superficie ou área calcúlase pola fórmula onde b é a lonxitude dun lado (a base) e h a altura respecto dese lado.
- A suma das lonxitudes de dous dos seus ángulos é sempre maior ca do terceiro lado.
- A suma dos seus ángulos é igual a 180º.
- Teorema de Pitágoras: nun triángulo rectángulo, a suma dos cadrados dos catetos é igual ao cadrado da hipotenusa: a² + b² = c²
- Teorema do seno: nun triángulo calquera, os lados son proporcionais aos senos dos ángulos opostos:
- Teorema do coseno: nun triángulo calquera, o cadrado dun lado é igual á suma dos cadrados dos outros lados menos o dobre do produto destes lados polo coseno do ángulo comprendido entre eles:
Tipos de triángulos[editar | editar a fonte]
O triángulo, en función dos seus lados, pode ser:
- Equilátero: cando o triángulo ten os seus tres lados (e polo tanto os seus ángulos) iguais.
- Isóscele: cando ten dous lados (e dous ángulos) iguais, e outro desigual.
- Escaleno: cando ten os tres lados (e ángulos) desiguais.
O triángulo, en función dos seus ángulos, pode ser:
- Acutángulo: cando ten os seus tres ángulos agudos (menores de 90 graos).
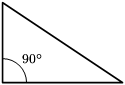
- Rectángulo: cando ten un ángulo recto (de 90 graos).
- Obtusángulo: cando ten un ángulo obtuso (maior de 90 graos).
O triángulo rectángulo[editar | editar a fonte]

- Artigo principal: triángulo rectángulo.
Un caso especial e amplamente estudado é o do triángulo rectángulo polas súas propiedades xeométricas. Neste tipo de triángulos, o lado oposto ó ángulo de 90 graos chámase hipotenusa, e os outros dous catetos. A área dun triángulo rectángulo pódese calcular como o produto (das lonxitudes) dos catetos dividido entre dous. Ademais, sempre se cumpre que o cadrado da hipotenusa é igual á suma dos cadrados dos catetos (propiedade enunciada no Teorema de Pitágoras).
Ademais, defínese o coseno dun ángulo como a lonxitude do cateto contiguo partido pola hipotenusa, e o seno como cateto oposto dividido entre a hipotenusa. A tanxente será a razón entre o cateto oposto e o contiguo, ou entre o seno e o coseno.
Se xuntamos dous triángulos rectángulos iguais superpoñendo as súas hipotenusas, a figura resultante é un rectángulo (de aí a relación entre o cálculo das áreas de ambas figuras). Se os triángulos unidos son, ademais de rectángulos, isósceles (os ángulos agudos son de 45 graos), resulta un cadrado.
Liñas e puntos notables dos triángulos[editar | editar a fonte]
- Altura e ortocentro: a altura dun triángulo é a perpendicular trazada dende un vértice ao seu lado oposto. O punto onde se cortan as tres alturas é o ortocentro.
- Mediana ou transversal de gravidade e baricentro: a mediana é a liña que une un vértice co punto medio do lado oposto. O punto de corte entre as tres medianas chámase baricentro.
- Mediatriz e circuncentro: levantando perpendiculares polo punto medio de cada un dos lados obtéñense as mediatrices. O punto no que se cortan as tres mediatrices é o circuncentro, e é o centro da circunferencia circunscrita ao triángulo.
- Bisectriz e incentro: a bisectriz dun ángulo é o lugar xeométrico dos puntos que equidistan dos lados. O incentro é o punto no que converxen as bisectrices dos vértices, e ademais é o centro da circunferencia inscrita no triángulo.
Véxase tamén[editar | editar a fonte]
| Wikimedia Commons ten máis contidos multimedia na categoría: Triángulo |




















