Ecuación diferencial

Unha ecuación diferencial é a relación entre unha ou máis variábeis e as súas derivadas.
As ecuación diferenciais divídense en dous grandes grupos, con técnicas de resolución diferentes:
- Unha ecuación diferencial ordinaria (EDO) contén apenas funcións dunha variábel e as súas derivadas.
- Por exemplo onde é a variábel dependente, a variábel independente e a derivada de con respecto a .
- Unha ecuación diferencial parcial (EDP) contén mais do que unha variábel e as súas derivadas parciais.
- Como .
Historia[editar | editar a fonte]
Aínda que desde os comezos da mecánica se utilizaron métodos para relacionar taxas de cambio, non é até o desenvolvemento do cálculo que se pode comezar a falar de ecuacións diferenciais, a expresión parece que foi utilizada por vez primeira por Leibniz en 1676 [1]. A primeira clasificación das ecuacións de primeira orde débese a Newton. A finais de século, os irmán Bernoulli introducen o concepto de integrar unha ecuación e o procedemento de separación de variábeis. Euler sistematiza estes traballos e varios posteriores e crea a primeira teoría da ecuacións diferenciais, que segue sendo útil hoxe, aínda que moi ampliada.
Resolución de ecuacións diferenciais[editar | editar a fonte]
Existen moitos métodos para resolver unha ecuación diferencial, porén non todas as ecuacións teñen solución, e non sempre se pode chegar a ela por métodos analíticos.
unha solución dunha ecuación diferencial é unha función que satisfai a ecuación diferencial para todos os valores de x nun intervalo de interese.[2]
Tipos[editar | editar a fonte]
As ecuacións diferenciais poden dividirse en varios tipos. Á parte de describir as propiedades da ecuación en si, as clases de ecuacións diferenciais poden axudar a facer a escolla da aproximación a unha solución. É moi común que estas distincións inclúan se a ecuación é Ordinaria/Derivadas Parciais, Linear/Non linear e Homoxénea/Non homoxénea.
Ecuacións diferenciais ordinarias[editar | editar a fonte]

Unha ecuación diferencial ordinaria (EDO) é unha ecuación que contén unha función dunha variable independente e as súas derivadas. O temo "ordinaria" emprégase como contraste coa ecuación en derivadas parciais que pode ser respecto a máis dunha variable independente.
As ecuacións diferenciais lineares, que teñen solucións que poden sumarse e ser multiplicadas por coeficientes, están ben definidas e comprendidas, e teñen solucións exactas que poden ser calculadas. En contraste, as EDOs cuxas solucións non poden sumarse son non lineares, e a súa solución é máis intricada, e moi poucas veces poden ser calculadas en forma exacta de funcións elementais: as solucións adoitan obterse en forma de series ou forma integral. Os métodos numéricos e gráficos para EDOs poden aproximar as solucións das ecuacións e o seu resultado pode ser moi útil, moitas veces suficientes como para prescindir da solución exacta e analítica.
Ecuación en derivadas parciais[editar | editar a fonte]

Unha ecuación en derivadas parciais (EDP) é unha ecuación diferencial que contén unha función multivariable e as súas derivadas parciais. Estas ecuacións empréganse para formular problemas que involucran funcións de varias variables, e poden resolverse manualmente, para crear unha simulación por ordeador.
As EDPs poden empregarse para describir unha ampla variedade de fenómenos como o son, a calor, a electrostática, a electrodinámica, a fluidodinámica, a elasticidade, ou a mecánica cuántica. Estes distintos fenómenos físicos poden formalizarse mediante EDPs. Con ecuacións diferenciais ordinarias é moi común realizar modelos unidimensionais de sistemas dinámicos, e as ecuacións diferenciais parciais poden empregarse para modelos de sistemas multidimensionais. As EDPs teñen unha xeneralización nas ecuacións en derivadas parciais estocásticas.
Ecuacións diferenciais lineares[editar | editar a fonte]
Unha ecuación diferencial é linear se a función descoñecida e as súas derivadas que aparecen son de potencia 1 (non se permiten os produtos da función descoñecida e as súas derivadas). A propiedade característica das ecuacións lineares é que as súas solucións teñen a forma dun subespazo afín dun espazo de solucións apropiados, cun resultado que se desenvolve na teoría das ecuacións diferenciais lineares.
As ecuacións diferenciais lineares homoxéneas son unha subclase das ecuacións diferenciais lineares para a que o espazo de solucións é un subespazo linear, é dicir, a suma de calquera conxunto de solucións ou múltiplos de solucións, é tamén unha solución. Os coeficientes da función descoñecida e as súas derivadas nunha ecuación diferencial linear poden ser funcións da variable ou variables independentes; se estes coeficientes son constantes, fálase de ecuacións diferenciais lineares con coeficientes constantes.
Dise que unha ecuación é linear se ten a forma:
É dicir:
- Nin a función nin as súas derivadas están elevadas a ningunha potencia distinta dun ou cero.
- En cada coeficiente que aparece multiplicándoas só intervén a variable independente.
- Unha combinación linear das súas solucións é tamén solución da ecuación.
Exemplos:
- é unha ecuación diferencial ordinaria linear de primeira orde, ten como solucións , con k un número real calquera.
- é unha ecuación diferencial ordinaria linear de segunda orde, en como solucións , con a e b reais.
- é unha ecuación diferencial ordinaria linear de segunda orde, ten como solucións , con a e b reais.
Ecuacións diferenciais non lineares[editar | editar a fonte]
Existen moi poucos métodos para resolver ecuacións diferenciais non lineares de forma exacta. As ecuacións diferenciais non lineares poden amosar un comportamento moi complicado en intervalos grandes de tempo, característica do caos. Cada unha das cuestións fundamentais da existencia, unicidade e extensibilidade das solucións para ecuacións diferenciais non lineares, e o problema das definicións das condicións iniciais e do contorno para EDPs non lineares son problemas difíciles e a súa resolución en casos especiais considérase que é un avance significativo na teoría matemática (por exemplo a existencia e suavidade de Navier-Stokes). Porén, se a ecuación diferencial é unha representación dun proceso físico significativo formulado correctamente, entón espérase que teña solución.[3]
As ecuacións diferenciais lineares adoitan aparecer por medio de aproximacións a ecuacións lineares. Estas aproximacións son válidas unicamente baixo condicións restrinxidas. Por exemplo, a ecuación do oscilador harmónico é unha aproximación da ecuación non linear dun péndulo que é válida para pequenas amplitudes de oscilación.
Ecuacións semilineares e cuasilineares[editar | editar a fonte]
Non existe un procedemento xeral para resolver ecuacións diferenciais non lineares. Non obstante, algúns casos particulares de non linearidade si se poden resolver. Son de interese o caso semilinear e o caso cuasilinear.
Unha ecuación diferencial ordinaria de orde n chámase cuasilinear se é "linear" na derivada de orde n. Máis especificamente, se a ecuación diferencial ordinaria para a función pode escribirse na forma:
dise que a ecuación é cuasilinear se é unha función afín, é dicir, .
Unha ecuación diferencial ordinaria de orde n chámase semilinear se pode escribirse como suma dunha función "linear" da derivada de orde n máis unha función calquera do resto de derivadas. Formalmente, se a ecuación diferencial ordinaria para a función pode escribirse na forma:
dise que a ecuación é semilinear se é unha función linear.
Orde da ecuación[editar | editar a fonte]
As ecuacións diferenciais descríbense pola súa orde, determinada polo termo con derivadas de maior orde. Unha ecuación que contén só derivadas simples é unha ecuación diferencial de primeira orde, unha ecuación que contén ata derivadas segundas é unhaecuación diferencial de segunda orde, e así sucesivamente.[4][5]
Exemplos de orde en ecuacións:
- Ecuación diferencial de primeira orde:
- Ecuación diferencial de segunda orde:
- Ecuación diferencial de terceira orde:
Grao da ecuación[editar | editar a fonte]
É a potencia da derivada de maior orde que aparece na ecuación, sempre e cando a ecuación estea en forma polinómica; de non ser así considérase que non ten grao.
Exemplos[editar | editar a fonte]
No primeiro grupo de exemplos, sexa u unha función descoñecida que depende de x, e c e ω son constantes coñecidas.
- Ecuación diferencial ordinaria linear con coeficientes constantes de primeira orde:
- Ecuación diferencial ordinaria linear homoxénea de segunda orde:

- Ecuación diferencial ordinaria linear con coeficientes constantes homoxénea de segunda orde que describe un oscilador harmónico:
- Ecuación diferencial ordinaria non linear non homoxénea de primeira orde:
- Ecuación diferencial ordinaria non linear (debido á función seno) de segunda orde, que describe o movemento dun péndulo de lonxitude L:
No seguinte grupo de exemplos, a función descoñecida u depende de dúas variables x e t ou x e y.
- Ecuación en derivadas parciais linear homoxénea de primeira orde:
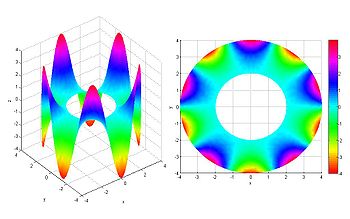
- Ecuación en derivadas parciais linear homoxénea con coeficientes constantes de segunda orde do tipo elíptico, a ecuación de Laplace:
- Ecuación en derivadas parciais non linear de terceira orde, a ecuación de Korteweg-de Vries:
Notas[editar | editar a fonte]
- ↑ "Historia de las ecuaciones diferenciales" (PDF). Arquivado dende o orixinal (PDF) o 06 de marzo de 2007. Consultado o 25 de novembro de 2007.
- ↑ Campell, Haberman, páxina 6
- ↑ Boyce, William E.; DiPrima, Richard C. (1967). Elementary Differential Equations and Boundary Value Problems (en inglés) (4ª ed.). John Wiley & Sons.
- ↑ Weisstein, Eric W. "Ordinary Differential Equation Order". MathWorld (en inglés).
- ↑ "Order and degree of a differential equation" (en inglés). Arquivado dende o orixinal o 01 de abril de 2016. Consultado o 4 de abril de 2016.
Véxase tamén[editar | editar a fonte]
| Wikimedia Commons ten máis contidos multimedia na categoría: Ecuación diferencial |
Bibliografía[editar | editar a fonte]
- Richard Bronson: Ecuaciones diferenciales modernas. McGraw-Hill Mexico 1988
- Frank Ayres: Ecuaciones diferenciales. McGraw-Hill Mexico
- Campbell, Haberman: Ecuaciones diferenciales McGraw-Hill Mexico 1996
- G. Boole A treatise on differential equations[Ligazón morta] (McMillan, Cambridge, 1859) (en inglés)
- W. W. Johnson A treatise on ordinary and partial differential equations. (J. Wiley & Sons, New York, 1889) (en inglés)
- E. Goursat A course of mathematical analysis, part II of volume II (Ginn & co. 1917) (en inglés)
- E. L. Ince Ordinary Differential Equations (Longman Greens, Londres, 1927) (en inglés)
- A. R. Forsyth A Treatise On Differential Equations (MacMillan, Londres, 1929) (en inglés)
- E. G. C. Poole Introduction To The Theory Of Linear Differential Equations (Clarendon Press, Oxford, 1936) (en inglés)
- E. Picard Traité d'Analyse (vol. 3) (Gauthier-Villars, 1896) (en francés)
- C. Jordan Cours d'Analyse de l'Ecole Polytechnique (vol. 3) (Gauthier-Villars, 1913) (en francés)






























