Combinación linear
En matemática, particularmente en álxebra linear, unha combinación linear é unha expresión matemática que consiste na suma entre pares de elementos de determinados conxuntos multiplicados entre si.
En particular, a combinación linear dun sistema de vectores trátase dun vector da forma
cos elementos dun corpo. A definición dá lugar a outras definicións e ferramentas importantes, como son os conceptos de independencia linear e base dun espazo vectorial.
Definición[editar | editar a fonte]
Dados dous conxuntos calquera A e B, defínese como combinación linear toda expresión da forma
Resulta de especial interese a definición de combinación linear de vectores con respecto a un conxunto de escalares.
Espazos vectoriais[editar | editar a fonte]
Dado un espazo vectorial V sobre un corpo e un conxunto de vectores en V, é dicir, , dise que un vector é combinación linear de A se .
En termos informais, dise que é combinación linear de vectores de se se poden expresar como unha suma de produtos por escalar dunha cantidade finita de elementos de . Neste caso, tamén se di que depende linearmente dos vectores de .[1]
Exemplos[editar | editar a fonte]
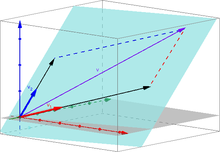
- A terna ordenada (20, 12, 37) é unha combinación linear de (1, 3, 5) e (6, 2, 9):
- En xeral, dado un vector v nun espazo vectorial, todo múltiplo seu é combinación linear. Para o caso particular , os seus múltiplos son vectores no plano coa mesma dirección, é dicir, paralelos.
- Dado , dicir que v é combinación linear doutros dous vectores non paralelos equivale a afirmar que o tres vectores son coplanarios, é dicir, que se atopan nun mesmo plano.
- Na ecuación dise que é combinación linear de e de porque se pode escribir sen máis que despexar . Do mesmo xeito, despexando oportunamente cada unha destas variables poderíase expresar como combinación linear das outras dúas.
Espazo xerado[editar | editar a fonte]
Dado un conxunto de vectores A do espazo vectorial V, finito ou infinito, chámase espazo xerado, denotado como , ao conxunto:[2]
onde é o corpo sobre o cal está definido V. En termos informais, o espazo xerado a partir de A é o conxunto de todas as combinacións lineares que poden formarse cos vectores de A.
Notas[editar | editar a fonte]
- ↑ De Burgos, Juan (2006). Álgebra lineal y geometría cartesiana (3.ª ed.). McGraw-Hill. p. 26. ISBN 9788448149000.
- ↑ Poole, David (2011). Álgebra lineal (en castelán) (3.ª ed.). Cengage Learning. p. 96. ISBN 9786074816082.
Véxase tamén[editar | editar a fonte]
Outros artigos[editar | editar a fonte]
- Independencia linear
- Base (álxebra)
- Sistema de coordenadas cartesianas
- Produto escalar
- Produto vectorial
- Produto mixto
- Produto tensorial






















