Forza

En física, a forza é unha magnitude física que mide a razón de cambio do momento lineal entre dúas partículas ou sistemas de partículas. Segundo unha definición clásica, forza é calquera acción ou influencia capaz de modificar a forma dos materiais ou a cantidade de movemento, producindo unha variación no estado de equilibrio ou de movemento dun corpo, é dicir, capaz de imprimirlle unha aceleración.
Matematicamente , onde p é o momento lineal. A aceleración que experimenta un corpo é, por definición, proporcional á suma das forzas (ou forza neta) que actúa sobre el. A constante de proporcionalidade entre a forza neta e a aceleración denomínase masa (inercial) do corpo. Estas dúas afirmacións resúmense na Lei Fundamental da Dinámica ou Segunda Lei de Newton:
onde representa as forzas que actúan sobre o corpo, a súa masa e a súa aceleración.
As forzas, ao igual que as aceleracións, son magnitudes vectoriais. As magnitudes vectoriais represéntanse matematicamente mediante vectores. A suma na Segunda Lei de Newton é, polo tanto, unha suma vectorial.
Posto que as forzas soamente modifican o estado de movemento dun corpo, para que un corpo se mova non é necesario que actúe sobre el unha forza. As forzas só son necesarias para pór en movemento un corpo que está inmóbil ou para alterar a velocidade dun que está en movemento. Un corpo en movemento sobre o que non actúa ningunha forza seguirá movéndose en liña recta e a velocidade constante indefinidamente. Este feito foi recollido en forma de lei por primeira vez por Newton, na chamada Lei da Inercia ou Primeira Lei de Newton. A observación de que para manter en movemento un corpo non é necesario exercer ningunha acción sobre el era radicalmente contraria á visión clásica, defendida por Aristóteles, que postulaba que un corpo sobre o que non se exercía ningunha influencia sempre terminaba por se deter. O cambio conceptual recollido na Lei da Inercia e o concepto de forza constituíu o punto de partida do desenvolvemento da dinámica moderna e, con ela, da física que hoxe coñecemos.
No Sistema Internacional de Unidades, a unidade de medida de forza é o newton que se representa co símbolo N, nomeada así en recoñecemento a Isaac Newton pola súa achega á física, especialmente á mecánica clásica. O newton é unha unidade derivada do Sistema Internacional de Unidades que se define como a forza necesaria para proporcionar unha aceleración de 1 m/s² a un obxecto de 1 kg de masa.
O concepto de forza non debe confundirse cos de esforzo ou de enerxía. O aparato que permite medir forzas denomínase dinamómetro.
Distintos aspectos da forza
[editar | editar a fonte]A forza é un modelo matemático de intensidade das interaccións, xunto coa enerxía. Así, por exemplo, a forza gravitacional é a atracción entre os corpos que teñen masa, o peso é a atracción que a Terra exerce sobre os obxectos nas proximidades da súa superficie, a forza elástica é o pulo ou tensión que exerce un resorte comprimido ou estirado, respectivamente etc. En física, hai dous tipos de ecuacións de forza: as "de causas", nas cales se especifica a orixe da atracción ou repulsión como, por exemplo, a lei da gravitación universal de Newton ou a lei de Coulomb; e as "de efectos", as cales son, fundamentalmente, formas da segunda lei de Newton.
A forza é unha magnitude física de carácter vectorial capaz de deformar os corpos (efecto estático), modificar a súa velocidade ou vencer a súa inercia, e poñelos en movemento se estaban inmóviles (efecto dinámico). Neste sentido, a forza pode definirse como toda acción ou influencia capaz de modificar o estado de movemento ou de reposo dun corpo (imprimíndolle unha aceleración que modifica o módulo ou a dirección da súa velocidade).
Comunmente referímonos á forza aplicada sobre un obxecto sen ter en conta ao outro obxecto u obxectos cos que está interactuando, e que experimentarán, á súa vez, outras forzas. Actualmente, cabe definir a forza como un ente fisicomatemático, de carácter vectorial, asociado coa interacción do corpo con outros corpos que constitúen a súa contorna.
Historia
[editar | editar a fonte]
O concepto de forza describiuno orixinariamente Arquímedes, se ben unicamente en termos estáticos. Arquímedes e outros creron que o "estado natural" dos obxectos materiais na esfera terrestre era o repouso e que os corpos tendían, por si mesmos, cara ese estado se non se actuaba sobre eles en modo algún. De acordo con Aristóteles, a perseveranza do movemento requiría sempre unha causa eficiente (algo que parece concordar coa experiencia cotiá, onde as forzas de fricción poden pasar desapercibidas).
Galileo Galilei (1564-1642) sería o primeiro en dar unha definición dinámica de forza, oposta á de Arquímedes, establecendo claramente a lei da inercia, afirmando que un corpo sobre o que non actúa ningunha forza permanece en movemento inalterado. Esta lei, que refuta a tese de Arquímedes, aínda hoxe en día non resulta obvia para a maioría das persoas sen formación científica.
Considérase que foi Isaac Newton o primeiro que formulou matematicamente a moderna definición de forza, aínda que tamén usou o termo latino vis impressa ('forza impresa') e vis motrix para outros conceptos diferentes. Ademais postulou que as forzas gravitatorias variaban segundo a lei da inversa do cadrado da distancia.
En 1784, Charles Coulomb foi o primeiro que comprobou que a interacción entre cargas eléctricas ou electrónicas puntuais tamén varía segundo a lei da inversa do cadrado da distancia.
En 1798, Henry Cavendish logrou medir experimentalmente a forza de atracción gravitatoria entre dúas masas pequenas utilizando unha balanza de torsión, grazas ao cal puido determinar o valor da constante da gravitación universal, que lle permitiu calcular a masa da Terra.
Co desenvolvemento da electrodinámica cuántica, a mediados do século XX, constatouse que a "forza" era unha magnitude puramente macroscópica xurdida da conservación do momento lineal ou cantidade de movemento para partículas elementais. Por esta razón, as chamadas forzas fundamentais adoitan denominarse "interaccións fundamentais".
Natureza vectorial das forzas
[editar | editar a fonte]A forza, ao igual que a velocidade ou a aceleración, é unha magnitude vectorial, que se caracteriza por ter:
- Módulo. Número positivo que indica a intensidade da forza.
- Dirección. Coincide coa da recta sobre a cal actúa.
- Sentido. Indica a súa orientación sobre a recta na que actúa.
- Punto de aplicación. Indica o punto no cal se aplica a forza[1].
Forza na mecánica newtoniana
[editar | editar a fonte]A forza pódese definir a partir da derivada temporal do momento linear:
Se a masa permanece constante, pódese escribir:
(*)
onde m é a masa e a a aceleración, que é a expresión tradicional da segunda lei de Newton. No caso da estática, onde non existen aceleracións, as forzas actuantes poden deducirse de consideracións de equilibrio.
A ecuación () é útil sobre todo para describir o movemento de partículas ou corpos cunha forma que non é relevante para o problema formulado. Pero mesmo se se trata de estudar a mecánica de sólidos ríxidos precísanse postulados adicionais para definir a velocidade angular do sólido, ou a súa aceleración angular así como a súa relación coas forzas aplicadas. Para un sistema de referencia arbitrario a ecuación () debe substituírse por:[2]
Onde:
Forzas de contacto e forzas a distancia
[editar | editar a fonte]Nun sentido estrito, todas as forzas naturais son forzas producidas a distancia como produto da interacción entre corpos; non obstante, dende o punto de vista macroscópico, adóitanse dividir as forzas en dos tipos xerais:
- Forzas de contacto, as que se dan como produto da interacción dos corpos en contacto directo; é dicir, impactando as súas superficies libres (como a forza normal).
- Forzas a distancia, como a forza gravitatoria ou a de Coulomb entre cargas, debida á interacción entre campos (gravitatorio, eléctrico etc.) e que se producen cando os corpos están separados certa distancia uns dos outros, por exemplo, o peso.
Forzas internas e de contacto
[editar | editar a fonte]
Nos sólidos, o principio de exclusión de Pauli conduce xunto coa conservación da enerxía a que os átomos teñan os seus electróns distribuídos en capas e teñan impenetrabilidade a pesar de estar baleiros nun 99 %. A impenetrabilidade derívase de que os átomos sexan "extensos" e que os electróns das capas exteriores exerzan forzas electrostáticas de repulsión que fan que a materia sexa macroscopicamente impenetrable.
O anterior tradúcese en que dous corpos postos en contacto experimentarán superficialmente forzas resultantes normais (ou aproximadamente normais) á superficie que impedirán o solapamento das nubes electrónicas de ambos os corpos.
As forzas internas son similares ás forzas de contacto entre ambos os corpos e se ben teñen unha forma máis complicada, xa que non existe unha superficie macroscópica a través da cal se dean a superficie. A complicación tradúcese por exemplo en que as forzas internas necesitan ser modelizadas mediante un tensor de tensións en que a forza por unidade de superficie que experimenta un punto do interior depende da dirección ao longo da cal se consideren as forzas.
O anterior refírese a sólidos, nos fluídos en repouso as forzas internas dependen esencialmente da presión, e nos fluídos en movemento tamén a viscosidade pode desempeñar un papel importante.
Fricción
[editar | editar a fonte]A fricción en sólidos pode darse entre as súas superficies libres en contacto. No tratamento dos problemas mediante mecánica newtoniana, a fricción entre sólidos frecuentemente modelízase como unha forza tanxente sobre calquera dos planos do contacto entre as súas superficies, de valor proporcional á forza normal.
O rozamento entre sólido-líquido e no interior dun líquido ou un gas depende esencialmente de se o fluxo se considera laminar ou turbulento e da súa ecuación constitutiva.
Forza gravitatoria (Newton)
[editar | editar a fonte]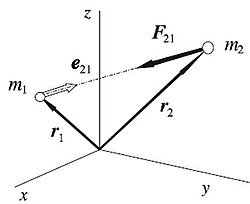
Na mecánica newtoniana a forza de atracción entre dúas masas, con centros de gravidade que están afastados comparados coas dimensións do corpo,[3] vén dada pola lei da gravitación universal de Newton:
Onde:
- é a forza que actúa sobre o corpo 2, exercida polo corpo 1.
- constante da gravitación universal.
- vector de posición relativo do corpo 2 respecto ao corpo 1.
- é o vector unitario dirixido dende 1 cara a 2.
- masas dos corpos 1 e 2.
Cando a masa dun dos corpos é moi grande en comparación coa do outro (por exemplo, se ten dimensións planetarias), a expresión anterior se transforma en outra máis simple:
Onde:
- é a forza dun corpo de gran masa (como un planeta ou unha estrela) sobre o corpo pequeno.
- é un vector unitario dirixido dende o centro do corpo de gran masa ao corpo de menor masa.
- é a distancia entre o centro do corpo de gran masa e o de menor masa.
Forzas de campos estacionarios
[editar | editar a fonte]Na mecánica newtoniana tamén é posible modelizar algunhas forzas constantes no tempo como campos de forza. Por exemplo a forza entre dúas cargas eléctricas inmóbiles, pode representarse adecuadamente mediante a lei de Coulomb:
Onde:
- é a forza exercida pola carga 1 sobre a carga 2.
- unha constante que dependerá do sistema de unidades para a carga.
- vector de posición da carga 2 respecto á carga 1.
- valor das cargas.
Tamén os campos magnéticos estáticos e os debidos a cargas estáticas con distribucións máis complexas poden resumirse en dúas funcións vectoriais chamadas campo eléctrico e campo magnético tales que unha partícula en movemento respecto ás fontes estáticas de devanditos campos vén dada pola expresión de Lorentz:
Onde:
- é o campo eléctrico.
- é o campo magnético.
- é a velocidade da partícula.
- é a carga total da partícula.
Os campos de forzas non constantes con todo presentan unha dificultade especialmente cando están creados por partículas en movemento rápido, porque neses casos os efectos relativistas de retardo poden ser importantes, e a mecánica clásica, dá lugar a un tratamento de acción a distancia que pode resultar inadecuado se as forzas cambian rapidamente co tempo.
Forza eléctrica
[editar | editar a fonte]A forza eléctrica tamén son de acción a distancia, pero ás veces a interacción entre os corpos actúa como unha forza atractiva mentres que, outras veces, ten o efecto inverso, é dicir pode actuar como unha forza repulsiva.
Unidades de forza
[editar | editar a fonte]No Sistema Internacional de Unidades (SI) e no Ceguesimal (CGS), o feito de definir a forza a partir da masa e da aceleración (magnitude en que interveñen lonxitude e tempo), implica que a forza sexa unha magnitude derivada. Polo contrario, no Sistema Técnico a forza é unha unidade fundamental e a partir dela defínese a unidade de masa neste sistema, a unidade técnica de masa, abreviada u.t.m. Este feito atende ás evidencias que posúe a física actual, expresado no concepto de forzas fundamentais.
- Sistema Internacional de Unidades (SI): newton (N)
- Sistema Técnico de Unidades: quilogramo-forza (kgf) ou quilopondio (kp)
- Sistema Ceguesimal de Unidades: dina (dyn)
- Sistema anglosaxón de unidades: poundal, libra forza (lbf) e KIP (= 1000 lbf)
- Equivalencias
- 1 newton = 100 000 dinas
- 1 quilogramo-forza = 9,806 65 newtons
- 1 libra forza ≡ 4,448 222 newtons
Forza en mecánica relativista
[editar | editar a fonte]Na relatividade especial a forza débese definir só como derivada do momento linear, xa que neste caso a forza non resulta simplemente proporcional á aceleración:
De feito en xeral o vector de aceleración e o de forza nin sequera serán paralelos, só no movemento circular uniforme e en calquera movemento rectilíneo serán paralelos o vector de forza e aceleración pero en xeral se o módulo da forza dependerá tanto da velocidade como da aceleración.
Forza gravitatoria (relatividade)
[editar | editar a fonte]Na teoría da relatividade xeral o campo gravitatorio non se trata como un campo de forzas real, senón como un efecto da curvatura do espazo-tempo. Unha partícula másica que non sofre o efecto de ningunha outra interacción que a gravitatoria seguirá unha traxectoria xeodésica de mínima curvatura a través do espazo-tempo, e polo tanto a súa ecuación de movemento será:
Onde:
- son as coordenadas de posición da partícula.
- o parámetro de arco, que é proporcional ao tempo propio da partícula.
- son os símbolos de Christoffel correspondentes á métrica do espazo-tempo.
A forza gravitatoria aparente procede do termo asociado aos símbolos de Christoffel. Un observador en "caída libre" formará un sistema de referencia en movemento no que eses símbolos de Christoffel son nulos, e polo tanto non percibirá ningunha forza gravitatoria tal como sostén o principio de equivalencia que axudou a Einstein a formular as súas ideas sobre o campo gravitatorio.
Forza electromagnética
[editar | editar a fonte]O efecto do campo electromagnético sobre unha partícula relativista vén dado pola expresión covariante da forza de Lorentz:
Onde:
- son as compoñentes covariantes da cuadriforza experimentada pola partícula.
- son as compoñentes do tensor de campo electromagnético.
- son as compoñentes da cuadrivelocidade da partícula.
A ecuación do movemento dunha partícula nun espazo-tempo curvo e sometida á acción da forza anterior vén dada por:
Onde a expresión anterior se aplicou o convenio de sumación de Einstein para índices repetidos, o membro da dereita representa a cuadriaceleración e sendo as outras magnitudes:
- son as compoñentes contravarianetes da cuadriforza electromagnética sobre a partícula.
- é a masa da partícula.
Forzas xeneralizadas
[editar | editar a fonte]O concepto de forza xeneralízase co uso de coordenadas xeneralizadas na mecánica de Lagrange como 'forzas xeneralizadas', definíndose
Forza en física cuántica
[editar | editar a fonte]Forza en mecánica cuántica
[editar | editar a fonte]Na mecánica cuántica non resulta fácil definir para moitos sistemas un equivalente claro da forza. Isto sucede porque na mecánica cuántica un sistema mecánico queda descrito por unha función de onda ou vector de estado que en xeral representa todo o sistema en conxunto e non pode separarse en partes. Só para sistemas onde o estado do sistema poida descompoñerse de xeito non ambiguo na forma onde cada unha desas dúas partes representa unha parte do sistema é posible definir o concepto de forza. Porén, na maioría de sistemas interesantes non é posible esta descomposición. Por exemplo se se considera o conxunto de electróns dun átomo, que é un conxunto de partículas idénticas non é posible determinar unha magnitude que represente a forza entre dous electróns concretos, porque non é posible escribir unha función de onda que describa por separado os dous electróns.
Con todo, no caso dunha partícula illada sometida á acción dunha forza conservativa é posible describir a forza mediante un potencial externo e introducir a noción de forza. Esta situación é a que se dá por exemplo no modelo atómico de Schrödinger para un átomo hidroxenoide onde o electrón e o núcleo son discernibles un do outro. Neste e noutros casos dunha partícula illada nun potencial o teorema de Ehrenfest leva a unha xeneralización da segunda lei de Newton na forma:
Onde:
- é o valor esperado do momento linear da partícula.
- é a función de onda da partícula e a súa complexa conxugada.
- é o potencial do que derivar as forzas.
- denota o operador nabla.
Noutros casos como os experimentos de colisión ou dispersión de partículas elementais de enerxía positiva que son disparados contra outras partículas que fan de albo, como os experimentos típicos levados a cabo en aceleradores de partículas ás veces é posible definir un potencial que está relacionado coa forza típica que experimentará unha partícula en colisión, pero aínda así en moitos casos non pode falarse de forza no sentido clásico da palabra.
Forzas fundamentais na teoría cuántica de campos
[editar | editar a fonte]Na teoría cuántica de campos, o vocábulo "forza" ten un sentido lixeiramente diferente ao que ten na mecánica clásica debido á dificultade específica sinalada na sección anterior de definir un equivalente cuántico das forzas clásicas. Por esa razón a expresión "forza fundamental" na teoría cuántica de campos refírese ao modo de interacción entre partículas ou campos cuánticos, máis que a unha medida concreta da interacción de dúas partículas ou campos.
A teoría cuántica de campos trata de dar unha descrición das formas de interacción existentes entre as diferentes formas de materia ou campos cuánticos existentes no universo. Así, a expresión "forzas fundamentais" refírese actualmente aos modos claramente diferenciados de interacción que coñecemos. Cada forza fundamental quedará descrita por unha teoría diferente e postulará diferentes lagranxianos de interacción que describan como é ese modo peculiar de interacción.
Cando se formulou a idea de forza fundamental considerouse que existían catro forzas fundamentais: a gravitatoria, a electromagnética, a nuclear forte e a nuclear débil. A descrición das forzas fundamentais tradicionais é a seguinte:
- A gravitatoria é a forza de atracción que unha masa exerce sobre outra, e afecta a todos os corpos. A gravidade é unha forza moi débil e dun solo sentido, pero de alcance infinito.
- A forza electromagnética afecta aos corpos electricamente cargados, e é a forza involucrada nas transformacións físicas e químicas de átomos e moléculas. É moito máis intensa que a forza gravitatoria, pode ter dous sentidos (atractivo e repulsivo) e o seu alcance é infinito.
- A forza ou interacción nuclear forte é a que mantén unidos os compoñentes dos núcleos atómicos, e actúa indistintamente entre dous nucleóns calquera, protóns ou neutróns. O seu alcance é da orde das dimensións nucleares, pero é máis intensa cá forza electromagnética.
- A forza ou interacción nuclear débil é a responsable da desintegración beta dos neutróns; os neutrinos son sensibles unicamente a este tipo de interacción (á parte da gravitatoria) electromagnética e a súa alcance é aínda menor que o da interacción nuclear forte.
Porén, cómpre sinalar que o número de forzas fundamentais no sentido anteriormente exposto depende do noso estado de coñecemento, así ata finais dos anos 1960 a interacción débil e a interacción electromagnética considerábanse forzas fundamentais diferentes, mais os avances teóricos permitiron establecer que en realidade ambos tipos de interacción eran manifestacións fenomenoloxicamente diferentes da mesma forza fundamental, a interacción electrodébil. Tense a sospeita de que en última instancia todas as forzas fundamentais son manifestacións fenomenolóxicas dunha única forza que sería descrita por algún tipo de teoría unificada ou teoría do todo.
Notas
[editar | editar a fonte]- ↑ Física y química. Anaya. 2012.
- ↑ W. Noll (2007): "On the concept of Force"
- ↑ Se esta condición non se cumpre a expresión resultante é diferente debido a que as zonas máis próximas entre corpos teñen unha influencia maior que as zonas máis afastadas.
Véxase tamén
[editar | editar a fonte]| Wikimedia Commons ten máis contidos multimedia na categoría: Forza |
Outros artigos
[editar | editar a fonte]- Unidade de medida
- Metroloxía
- Sistema Internacional de Unidades
- Sistema inglés
- Sistema ceguesimal
- Forza electrostática
- Forza electromagnética
- Forza de Coriolis
- Forza gravitacional






























![{\displaystyle \mathbf {F} ={\frac {d}{dt}}\left({\frac {m\mathbf {v} }{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}\right)={\frac {m\mathbf {v} }{\left[1-{\frac {v^{2}}{c^{2}}}\right]^{3/2}}}\left({\frac {\mathbf {v} }{c^{2}}}\cdot \mathbf {a} \right)+{\frac {m\mathbf {a} }{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a4906883865776a7bca11426d8de904d1cee2b2)



















