Frecuencia


Frecuencia é un termo empregado nas matemáticas e na física para indicar a velocidade de repetición de calquera fenómeno periódico. Defínese como o número de veces que se repite un fenómeno na unidade de tempo.
A unidade de medida da frecuencia é o hertz (Hz), onde 1 Hz é un suceso que ten lugar unha vez por segundo. Esta unidade era orixinariamente «ciclo por segundo» (cps), hai outras unidades para indicar a frecuencia de revolucións por minuto (rpm), ou para indicar as pulsacións do corazón e o tempo musical, os «pulsos por minuto» (bpm, do inglés beats per minute).
Definicións
[editar | editar a fonte]
Para procesos cíclicos como a rotación, as oscilacións ou as ondas, a frecuencia defínese como o número de ciclos por unidade de tempo. En disciplinas da física e a enxeñaría como a óptica, a acústica ou a radio, adoita denotarse a frecuencia coa letra latina f ou a grega ou ν (ni). A relación entre a frecuencia e o período dun suceso que se repite ou dunha oscilación vén dada por
Unidades
[editar | editar a fonte]A unidade derivada do Sistema Internacional para a frecuencia é o hertz (Hz), que recibe o seu nome polo físico alemán Heinrich Hertz; un hertz significa que o suceso se repite unha vez cada segundo. Previamente a unidade denominouse ciclo por segundo (cps).
A unidade tradicional da medida empregada para a rotación en aparellos mecánicos é revolucións por minuto, que se abrevia r/min ou rpm. 60 rpm equivale a un hertz.[1]
Frecuencias de ondas
[editar | editar a fonte]A frecuencia dunha onda é a cantidade de veces que alcanza a súa amplitude máxima (ou mínima) polo tempo transcorrido, que garda unha relación inversa co concepto de lonxitude de onda, a maior frecuencia, menor lonxitude de onda e viceversa. A frecuencia f é igual á velocidade v da onda, dividida pola lonxitude de onda λ (lambda):
Período e frecuencia
[editar | editar a fonte]Por unha cuestión de conveniencia, as ondas máis longas e lentas, como as ondas do mar, tenden a ser descritas a partir do período no canto da frecuencia. Pola contra, as ondas máis curtas, como as sonoras ou as de radio (o espectro radioeléctrico), adoitan ser descritas baseándose na súa frecuencia. Estas convencións móstranse na seguinte táboa:
| Frecuencia (hertz) | 1 mHz (10-3) | 1 Hz (100) | 1 kHz (103) | 1 MHz (106) | 1 GHz (109) | 1 THz (1012) |
|---|---|---|---|---|---|---|
| Período (segundo) | 1 ks (103) | 1 s (100) | 1 ms (10-3) | 1 µs (10-6) | 1 ns (10-9) | 1 ps (10-12) |
Frecuencia de mostraxe
[editar | editar a fonte]- Artigo principal: Frecuencia de mostraxe.
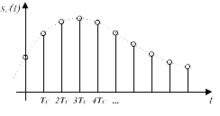
A frecuencia de mostraxe é un dos parámetros básicos que caracterizan o proceso de conversión analóxico-dixital nos sistemas electrónicos de procesamiento de información. Nun sistema electrónico, a información ten que ser codificada nun sinal eléctrico que varía a súa voltaxe co tempo. Falamos de sinal analóxico se varía continuamente no tempo, e de sinal dixital se só presenta un número finito de valores discretos ó longo do tempo. O proceso de mostraxe consiste a converter un sinal analóxico nun sinal dixital medindo e gravando, en momentos específicos do tempo (instantes de mostra), o valor instantáneo do sinal analóxico. A secuencia destes valores, as mostras tomadas, é o sinal dixital. O dispositivo que realiza a conversión de analóxico a dixital do sinal é un conversor analóxico-dixital. A frecuencia de mostraxe é o número de mostras gravadas nun segundo: o Teorema de mostraxe de Nyquist-Shannon, establece que, para que poidamos reconstruír o sinal analóxico a partir das mostras, fai falta que a frecuencia de mostraxe sexa como mínimo o dobre da frecuencia máis alta do sinal analóxico que se tenta dixitalizar:.
Frecuencia angular
[editar | editar a fonte]- Artigo principal: Frecuencia angular.
En electrodinámica clásica, na física teórica e nalgunhas aplicacións é conveniente utilizar un concepto adicional, a frecuencia angular. É unha cantidade física escalar que mide a frecuencia do movemento de vibración ou rotación. No caso do movemento de rotación, a frecuencia angular é igual ó módulo da velocidade angular. No SI e no CGS, mídese en radiáns por segundo, e a súa magnitude é a do inverso do tempo (os radiáns son adimensionais). A relación entre a frecuencia angular ω e a frecuencia f é: ω = 2πf.
No caso de que midamos os ángulos en graos, a relación é ω = 360°·f.
Numericamente, a frecuencia angular representa o número de ciclos (ou vibracións, ou rotacións) por cada 2π segundos. A introdución do concepto de frecuencia angular (na súa dimensión básica, radiáns por segundo) permite simplificar moitas das fórmulas da física teórica e a electrónica. Así, a frecuencia angular da resonancia dun circuíto LC é , mentres que a frecuencia ordinaria de resonancia é . O aspecto a favor da frecuencia angular é que os factores 2π e 1 / (2π), que aparecen en moitas das fórmulas (cando se utilizan os radiáns como unidade de medida de ángulos), desaparecen coa introdución da frecuencia angular.
Frecuencia na música
[editar | editar a fonte]En música, os sons audibles caracterízanse por unha cantidade fisiolóxica: a altura, que é, sinxelamente, a frecuencia fundamental do son correspondente. A altura tamén se expresa en hertzs (Hz). O espectro de frecuencias audibles polo oído humano esténdese desde os 20 Hz aos 20000 Hz aproximadamente.
Por convención, escolleuse a frecuencia de 440 Hz como a frecuencia de referencia para afinar os instrumentos musicais. O motivo é que esta é a frecuencia da nota La3: a nota musical "La" na terceira oitava.
Desde o punto de vista matemático, é posible realizar varios cálculos entre as notas musicais e as súas frecuencias. Se duplicamos unha frecuencia obtemos unha oitava, mentres que se sumamos unha frecuencia e a da súa oitava inferior obtemos unha quinta. Entón, a suma de dúas oitavas inferiores dános unha terceira maior. Por exemplo:
| Frecuencia | Nota | Intervalo | Cálculo |
|---|---|---|---|
| 110 | La1 | Oitava | 440/4 |
| 220 | La2 | Oitava | 440/2 |
| 440 | La3 | Oitava | (referencia) |
| 550 | Do# | Terceira Maior | 440 + 110 |
| 660 | Mi | Quinta xusta | 440 + 220 |
| 990 | Si | Quinta xusta (Mi-Si) | 660 + 330 |
Aínda así, temos que considerar que estes intervalos son puros e non temperados.
Frecuencia en matemáticas
[editar | editar a fonte]En teoría da probabilidade
[editar | editar a fonte]No marco da teoría da probabilidade a frecuencia relativa dun acontecemento é un dos conceptos fundamentais, xunto coa probabilidade real. Terminoloxicamente defínese como a relación entre o número de mostras que cumpren un certo acontecemento, respecto ó número total de mostras realizadas. A frecuencia relativa do acontecemento pode ser calculada só despois da mostraxe. A frecuencia relativa caracterízase pola estabilidade: de acordo cos resultados das observacións, para un número bastante grande de experimentos levados a cabo en condicións idénticas, o indicador non cambia e flutúa ó redor dunha certa constante.[2]
En estatística matemática
[editar | editar a fonte]- Artigo principal: Frecuencia (estatística).

En estatística pódense distinguir até catro tipos de frecuencias:
- Frecuencia absoluta É a media dunha suma predeterminada e, ademais, consiste en saber quen é o número ou símbolo de equivalencia máis grande. (ni) dunha variable estatística Xi, é o número de veces que este valor aparece no estudo. Canto maior é a mostra, máis aumentará o valor da frecuencia absoluta; é dicir, a suma total de todas as frecuencias absolutas ten que dar o total da mostra estudada (N).
- Frecuencia relativa (fi), é o cociente entre a frecuencia absoluta e a medida da mostra (N). É dicir,
- sendo os fi para todo o conxunto de valores i. Preséntase nunha táboa ou nube de puntos nunha distribución de frecuencias.
- Se multiplicamos a frecuencia relativa por 100 obtense a porcentaxe (pi)
- Frecuencia absoluta acumulada (Ni), é o número de veces ni na mostra N.
- Frecuencia relativa acumulada (Fi), é o cociente entre a frecuencia absoluta acumulada Ni respecto da mostra N
Outros tipos de frecuencia
[editar | editar a fonte]A frecuencia angular ω defínese como a taxa de variación do movemento angular, θ, (durante a rotación), ou a taxa de variación da fase da forma de onda senoidal (por exemplo, oscilacións e ondas), ou como a taxa de alteración do argumento da función seno:
A frecuencia angular mídese normalmente en radiáns por segundo (rad/s), mais, para os sinais de tempo discreto, pode tamén expresarse como radiáns por tempo de mostraxe, que é unha cantidade adimensional.
A frecuencia espacial é análoga á frecuencia temporal, mais o eixe do tempo substitúese por un ou máis eixes do movemento espacial. Por exemplo:
onde o número de onda, k, ten como unidade no SI radiáns por metro (rad/m). No caso de máis dunha dimensión espacial, o número de onda é unha magnitude vectorial.
Metroloxía
[editar | editar a fonte]Para medir a frecuencia úsanse frecuenciómetros de diferentes tipos, incluíndo: para medir a frecuencia dos polos - con electróns e condensador, para determinar as frecuencias dos compoñentes espectrais -, resonancia, contadores de frecuencia heterodina e analizadores de espectro. Para reproducir unha frecuencia determinada con precisión utilizando diferentes medidas (patróns de frecuencia de alta precisión), sintetizadores de frecuencia, xeradores de sinaisetc. Pódense comparar as medidas cun comparador de frecuencia ou utilizar un osciloscopio usando a curva de Lissajous.
Cálculos
[editar | editar a fonte]O cálculo da frecuencia do acontecemento pode obterse contando o número de ocorrencias do acontecemento nun prazo determinado de tempo. O número resultante divídese pola lonxitude do intervalo de tempo correspondente. Por exemplo, se nun período de 15 segundo obtense unha medida homoxénea de 71 acontecementos, a frecuencia será:
Se o número de mostras é pequeno, unha técnica máis precisa é medir o intervalo de tempo para un número predeterminado de ocorrencias do acontecemento, e non contar o número de acontecementos dentro dun período predeterminado.[3]
Utilizando este último método introdúcese entre o cero e a primeira lectura aleatoria de erro medianas marco, e isto pode dar lugar a erros na frecuencia mediana calculada Δf = 1/(2 Tm), ou un erro relativo de Δf / f = 1/(2 f Tm), onde Tm é o intervalo de tempo, e f - a frecuencia de medición. O erro diminúe a medida que a frecuencia aumenta, de forma que o problema é máis significativo nas frecuencias baixas, onde o número de mostras 'N' é pequeno.
Uso de estroboscopios
[editar | editar a fonte]O uso dun estroboscopio, dispositivo especial que xera escintileos brillantes de luz intermitente cunha temporización previamente calibrada, permite calcular a frecuencia de obxectos en vibración ou con movementos rotatorios. A fonte de luz diríxese ao obxecto en rotación, e auméntase ou diminúese gradualmente a frecuencia dos raios. Cando a frecuencia da luz estroboscópica se equipara coa frecuencia de rotación ou vibración do obxecto, é dicir cando un ciclo completo de oscilación con regreso á posición orixinal prodúcese no intervalo entre dous escintileos, a luz estroboscópica sobre o obxecto parece estacionaria. A partir de aquí, o valor obtido da frecuencia pódese ler coas diferentes lecturas. Este método, porén, ten un inconveniente: se a velocidade do obxecto (x) é igual á luz estroboscópica de frecuencia (e), pero a proporcionalidade é un número enteiro (2x, 3x, etc.), posto que o obxecto baixo estas situacións devolve unha iluminación que parece estática.
Uso de frecuenciómetros
[editar | editar a fonte]As frecuencias altas mídense normalmente cun frecuenciómetro. É un dispositivo electrónico que avalía a frecuencia dun certo sinal repetitivo, e mostra o resultado en hertzs nunha pantalla dixital. Os procesos cíclicos que non son inherentemente eléctricos (por exemplo, a frecuencia de rotación ó redor dun eixe, vibracións mecánicas ou ondas de son) poden converterse previamente nun sinal eléctrico (mediante algún tipo de transdutor), e entón tratalo da forma normal. Na actualidade, estes dispositivos son capaces de alcanzar un rango de até 100 GHz (na práctica, esta cantidade supón un límite polos métodos directos de medición). As frecuencias máis altas mídense mediante técnicas indirectas.
Técnicas indirectas de medición
[editar | editar a fonte]Ademais dos contadores de frecuencia habituais, a miúdo mídense indirectamente os sinais electromagnéticos mediante osciladores locais (é dicir, conversores de frecuencia). Se partimos dun sinal de referencia coñecido, e combinámolo cun mesturador de frecuencia non-lineal (por exemplo un díodo), obtemos un sinal heterodino, ou alternativamente obsérvase unha diferenza de frecuencia entre os dous sinais da fonte. Se esta diferenza é suficientemente pequena, o sinal resultante pode ser captado polo mesmo contador. En consecuencia, mediante este proceso pódese estimar a diferenza da frecuencia respecto do sinal coñecido e, polo tanto, a frecuencia do sinal orixinal. Se se necesita chegar a frecuencias máis altas, pódense empregar sucesivas etapas de mesturado. Na actualidade, está a investigarse a aplicación deste método indirecto nos sinais na banda do infravermello e o espectro visible.
Exemplos
[editar | editar a fonte]| Banda espectral | Frecuencia (Hz) |
|---|---|
| raios gamma | > 30,0 EHz |
| raios X | > 30,0 PHz |
| ultravioleta distante | > 1,5 PHz |
| ultravioleta próximo | > 789 THz |
| luz visible | > 384 THz |
| infravermello próximo (NIR) | > 120 THz |
| infravermello mediano (MIR) | > 6,00 THz |
| infravermello distante ou submilimétrico (FIR) | > 300 GHz |
| microondas | > 1,0 GHz |
| radio frecuencia ultraalta (UHF) | > 300 MHz |
| radio frecuencia moi alta (VHF) | > 30 MHz |
| radio de onda curta | > 1,7 MHz |
| radio de onda media | > 650 kHz |
| radio de onda longa | > 30 kHz |
| radio de frecuencia moi baixa (VLF) | < 30 kHz |
Radiación electromagnética
[editar | editar a fonte]A radiación electromagnética propágase en forma de ondas transportando enerxía. Este tipo de radiación inclúe desde a luz visible ás ondas de radio, pasando polas microondas. A luz visible que percibimos cos nosos ollos é só unha pequena fracción do espectro electromagnético e está composta por un certo número de cores (violeta, azul, ciano, verde, amarelo, laranxa, vermello) que corresponden a certos intervalos de frecuencias. Na táboa da dereita móstranse algunhas frecuencias do espectro electromagnético, e na de abaixo as frecuencias das diferentes cores da luz visible.
| Cor | Intervalo de frecuencia |
|---|---|
| violeta | ~ 790 a 700 THz |
| azul | ~ 700 a 600 THz |
| ciano | ~ 600 a 580 THz |
| verde | ~ 580 a 530 THz |
| amarelo | ~ 530 a 510 THz |
| laranxa | ~ 510 a 480 THz |
| vermello | ~ 480 a 405 THz |
A radiación ultravioleta (habitualmente simbolizada como UV) que nos chega do Sol é un exemplo común de radiación que non é visible para os nosos ollos. A pesar de non ser visible aféctanos, e por iso utilizamos filtros especiais nos nosos lentes de sol e cremas para protexernos dos seus efectos.
Outra propiedade das ondas electromagnéticas é a lonxitude de onda. A lonxitude de onda é inversamente proporcional á frecuencia, de tal maneira que as ondas electromagnéticas de frecuencia máis alta teñen unha lonxitude de onda curta e viceversa. No baleiro, a lonxitude de onda descríbese como
onde c é a velocidade da luz. Nunha contorna no cal a velocidade da velocidade de fase sexa c diferente da velocidade no baleiro (c = c / n, e n o índice de refracción), a relación entre a lonxitude de onda e a frecuencia é:
Outra característica é o número de onda, que é igual ó número de veces que vibra unha onda nunha unidade de distancia: k = 1 / λ. A miúdo, este valor multiplícase polo factor 2π, por analoxía coa frecuencia circular habitual, ks = 2π / λ. No caso da onda electromagnética:
Son
[editar | editar a fonte]O son é unha sucesión de cambios de presión nun medio (sólido, líquido ou gas), provocados por unha vibración que se transmite en forma de ondas sonoras, que son ondas mecánicas. Estas ondas caracterízanse tamén por unhas frecuencias que son captadas polo oído. No caso dos humanos as frecuencias audibles atópanse entre os 20 e os 20.000 hertzs (20 kHz), a pesar de que estes límites varían de maneira decrecente ó aumentar a idade, especialmente para as frecuencias altas.[4] Outras especies animais teñen outros intervalos de frecuencias audibles, os cans, por exemplo, poden percibir sons a frecuencias superiores ós 20 kHz.
Electricidade
[editar | editar a fonte]
Unha das características que definen a corrente alterna é a súa frecuencia, en Europa, África, Australia, a maior parte de Asia e parte de América do Sur utilízanse alternadores que producen electricidade de 50 Hz. Mentres que en Norteamérica e a parte norte de Suramérica utilizan unha frecuencia de 60 Hz. A frecuencia que xera o alternador depende do número de polos e do número de voltas por minuto.
Case tódolos aparellos eléctricos do fogar funcionan igual de ben en redes cunha frecuencia de 50 Hz e de 60 Hz, sempre que teñan a mesma voltaxe. A finais do século XIX e na primeira metade do século XX, antes da normalización, existían varias redes illadas con frecuencias que ían desde o 16 2⁄3 Hz até o 133 1⁄3 Hz.
Na rede a bordo das aeronaves, submarinos, etc. utilízase a frecuencia de 400 Hz. Esta maior frecuencia posibilita reducir o peso e o tamaño dos transformadores, aínda que aumenta a perda de transmisión a través de longas distancias.
Para determinar a frecuencia da corrente alterna producida por un xerador eléctrico, utilízase a seguinte ecuación:
,
onde F é a frecuencia (en Hz), P é o número de polos (sempre teñen que ser parellos), e Vg é a velocidade de xiro (en rpm).
Frecuencias especiais
[editar | editar a fonte]Hai algúns intervalos de frecuencias que debido á súa utilización ou características reciben un nome especial:
- Audiofrecuencia: Refírese ó rango de frecuencias das ondas sonnoras, de tipo mecánico, que son audibles polos humanos, este intervalo vai dos 20*Hz ós 20.000 Hz.
- Alta frecuencia: O termo é amplamente utilizado no campo das telecomunicacións e refírese a frecuencias entre os 3 e os 30 MHz. Noutros campos as frecuencias poden diferir.
- Frecuencias preferentes: Son un conxunto de intervalos de frecuencias normalizadas definidas na norma EN ISO 266 que se utilizan para medicións acústicos e nas disposicións legais.
Rangos de frecuencias
[editar | editar a fonte]Moitos sistemas caracterízanse polo rango de frecuencia ó que responden. Varios poden darse varios exemplos, os instrumentos musicais que producen rangos de notas diferentes, o espectro que se divide en varios rangos, por exemplo o visible, os infravermellos, os raios X..., e as emisoras de radio, cada unha ocupa un rango de frecuencia determinado... O rango de frecuencia dun sistema é o rango onde se considera que se ofrece un nivel útil do sinal con características de distorsión aceptables. Unha listaxe dos límites superior e inferior dos límites de frecuencia para un sistema non é útil sen saber que representa o rango. Tamén se pode falar de anchura de banda cando se fai referencia ó rango de frecuencias dun sinal analóxico.
Notas
[editar | editar a fonte]- ↑ Davies, A. (1997). Handbook of Condition Monitoring: Techniques and Methodology. Nova York: Springer. ISBN 978-0-412-61320-3.
- ↑ Gmurman, V. E. (2005). Teoriia veroiatnostei i matematicheskaia statistika Uchebnoe posobie dlia vuzov. (en ruso) (11a ed. ed.). Moscova: Vysshaia shkola. ISBN 5-06-004214-6.
- ↑ Bakshi, U.A; Bakshi, A.V. (2009). Electronic Measurement Systems (en inglés). Technical. pp. páx. 4–14. ISBN 9788184316032. Arquivado dende o orixinal o 30 de maio de 2020. Consultado o 25 de setembro de 2018.
- ↑ Ás veces tómase a fronteira entre os sons audibles e os infrasón nos 16 Hz.
Véxase tamén
[editar | editar a fonte]| Wikimedia Commons ten máis contidos multimedia na categoría: Frecuencia |
Bibliografía
[editar | editar a fonte]- Giancoli, D.C. (1988). Physics for Scientists and Engineers (2nd ed.). Prentice Hall. ISBN 0-13-669201-X.
Outros artigos
[editar | editar a fonte]- Frecuencia angular.
- Onda, lonxitude de onda, amplitude, frecuencia de corte.
- Espectro de frecuencia, espectro electromagnético.
- Nota musical.
Ligazóns externas
[editar | editar a fonte]- Conversion: frequency to wavelength and back Arquivado 11 de marzo de 2012 en Wayback Machine.
- Conversion: period, cycle duration, periodic time to frequency
- Keyboard frequencies = naming of notes - The English and American system versus the German system
- Teaching resource for 14-16yrs on sound including frequency Arquivado 13 de marzo de 2012 en Wayback Machine.
- A simple tutorial on how to build a frequency meter
- Frequency - diracdelta.co.uk – JavaScript calculation.
- A frequency generator with sound, useful for hearing tests




















