Radián

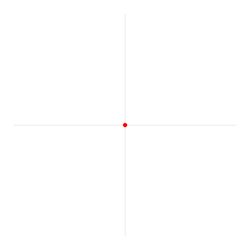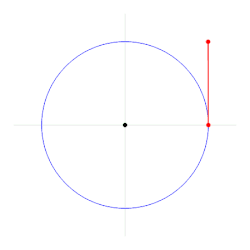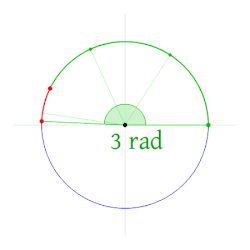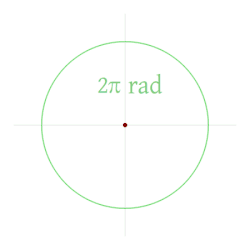
O radián é a unidade do ángulo plano no Sistema Internacional de Unidades. Enténdese por radián o ángulo no que a medida do arco é igual á medida do raio nunha circunferencia, situando o ángulo no centro. O Seu símbolo é rad.

Até 1995 tivo a categoría de unidade suplementaria no Sistema Internacional de Unidades, como o estereorradián. A partir dese ano, e até o presente, ambas unidades figuran na categoría de unidades derivadas.

Emprégase primordialmente na Física, no cálculo infinitesimal, na trigonometría, na goniometría etc.

Ángulos dos polígonos máis comúns medidos en radiáns, expresados como fraccións de π.

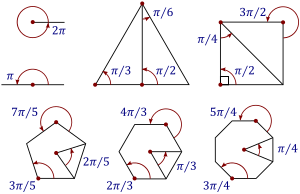
É unha medida moi útil para medir ángulos, posto que pode simplificar os cálculos, xa que os ángulos máis comúns exprésanse mediante múltiplos de π. Outras unidades de medida de ángulos convencionais son o grao sesaxesimal, o grao centesimal e, na astronomía, a hora.

Definición

Un radian é igual ao ángulo que forman dous raios dunha circunferencia cando abranguen un arco da mesma medida que o raio.

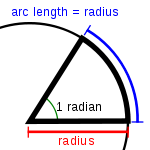
O ángulo formado por dous raios dunha circunferencia, medido en radiáns, é igual á lonxitude do arco que abranguen os raios; é dicir, θ = a /r, sendo θ o ángulo, a a lonxitude do arco, e r o raio. Entón, o ángulo completo, $\scriptstyle {\theta }_{\text{circunferencia}}$, que ten unha circunferencia de radio r, en radiáns, é:

$\theta _{\text{circunferencia}}={\frac {L_{\text{circunferencia}}}{r}}={\frac {2\pi r}{r}}=2\pi \ {\text{rad}}\,$

Equivalencias

• A equivalencia entre graos sesaxesimais e radiáns é: π rad = 180°
• A equivalencia entre graos centesimais e radiáns é: π rad = 200^g

A táboa amosa a conversión dos ángulos máis comúns.

Graos

0°

30°

45°

57,3°

60°

90°

114,6°

120°

135°

150°

171,9°

180°

210°

225°

229,2°

240°

270°

286,5°

300°

315°

330°

343,8°

360°

Radiáns

0

π/6

π/4

1

π/3

π/2

2

2π/3

3π/4

5π/6

3

π

7π/6

5π/4

4

4π/3

3π/2

5

5π/3

7π/4

11π/6

6

2π

Táboa de conversión entre graos sesaxesimais e radiáns.

O radián ten unha unidade derivada chamada radián por segundo (rad/s). Esta ten unha equivalencia coas rpm (revolucións por minuto). As equivalencias pódense calcular rapidamente coa fórmula que segue: De rpm a rad/s:

${\frac {rpm}{60}}\cdot 2=\pi rad/s$ que simplificando:${\frac {rpm}{30}}=\pi rad/s$

De rad/s a rpm:
${\frac {\pi rad/s}{2}}\cdot 60=rpm$ que simplificando:$\pi rad/s\cdot 30=rpm$

---

Este artigo sobre matemáticas é, polo de agora, só un bosquexo. Traballa nel para axudar a contribuír a que a Galipedia mellore e medre.  Existen igualmente outros artigos relacionados con este tema nos que tamén podes contribuír.

---