Función

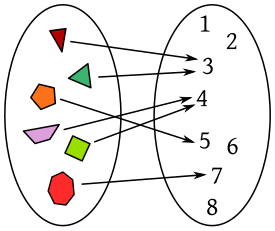
Para outras páxinas con títulos homónimos véxase: Función (homónimos).

Unha función vista como unha «caixa negra», que transforma os valores ou obxectos de «entrada» nos valores ou obxectos de «saída»

O concepto de función é unha xeneralización da noción común de fórmula matemática. As funcións ou aplicacións describen relacións matemáticas especiais entre dous obxectos, x e y=f(x). O obxecto x chámase o argumento da función f e o obxecto y, que depende de x, chámase imaxe de x en f.

Intuitivamente, unha función é un xeito de asociar a cada valor do argumento x un único valor da función f(x). Isto pódese facer especificando a través dunha fórmula, unha relación gráfica entre diagramas representando os dous conxuntos, ou dunha regra de asociación, mesmo pódese construír cunha táboa de correspondencia. Entre conxuntos numéricos é común representarmos funcións polos seus gráficos, cada par de elementos relacionados pola función determina un punto nesta representación, a restrición de unicidade da imaxe implica que existe un único punto para f en cada valor independente x. Este concepto é determinístico, sempre produce o mesmo resultado a partir dunha dada entrada (a xeneralización aos valores aleatorios é chamada de función estocástica). Unha función pode ser vista como unha "máquina" ou "caixa negra" que converte entradas válidas en saídas de forma unívoca, por iso algúns autores chaman ás funcións "relacións unívocas".

O tipo de función máis común é aquel onde o argumento e mailo valor da función son ambos numéricos, a relación entre os dous é expresado por unha fórmula e o valor da función obtense a través da substitución directa dos argumentos. Considérese o exemplo

f(x)=x^{2}

Que resulta en calquera valor de x ao cadrado.

Unha xeneralización directa é permitir que funcións dependan non só dun único valor, mais de varios. Por exemplo esta función de dúas variables,

g(x,y)=xy

recibe dous números x e y e resulta no produto deles, xy.

En base ao xeito en que se especifica unha función, esta pode chamarse función explícita (exemplo de riba) ou función implícita, como en

xf(x)=1

Función implícita

que implicitamente especifica a función

f(x)=1/x

Función explícita

Vimos que a noción intuitiva de funcións non se limita a computacións usando apenas números e tampouco se limita a computacións; a noción matemática de funcións é máis xeral e non se limita tampouco a situacións que inclúan números. En vez diso, unha función liga un "dominio" (conxunto de valores de entrada) cun segundo conxunto o "contra- dominio" (ou codominio) de tal forma que a cada elemento do dominio está asociado exactamente un elemento do contra-dominio, o conxunto dos elementos do contra-dominio que son relacionados pola f a algún x do dominio, chámase "conxunto-imaxe" ou "imaxe" . As funcións defínense abstractamente por certas relacións, como veremos mais adiante. Por causa da súa xeneralización, as funcións aparecen en moitos contextos matemáticos, e moitos campos da matemática baséanse no estudo de funcións.

Pode notarse que as palabras "función","aplicación", "transformación", "mapeado", "mapear" son xeralmente usadas como sinónimos.

Historia

Dirichlet foi quen introduciu a definición formal de función moderna.

Como un termo matemático, "función" foi introducido por Leibniz en 1694, para describir cantidades relacionadas a unha curva; tales como a inclinación da curva ou un punto específico da dita curva. Funcións relacionadas á curvas son actualmente chamadas funcións diferenciábeis e son aínda o tipo de funcións máis atopado por non-matemáticos. Para este tipo de funcións, pódese falar de límites e derivadas; ambos sendo medida da mudanza nos valores de saída asociados á variación dos valores de entrada, formando a base do cálculo infinitesimal.

A palabra función foi posteriormente usada por Euler a mediados do século XVIII para describir unha expresión comprendendo varios argumentos; i.e:y = F(x). Ampliando a definición de funcións, os matemáticos foron capaces de estudar "estraños" obxectos matemáticos tales como funcións que non son diferenciábeis en calquera dos seus puntos. Tales funcións, inicialmente tidas como puramente imaxinarias e chamadas xenericamente de "monstros", foron xa no final do século XX, identificadas como importantes para a construción de modelos físicos de fenómenos tales como o movemento Browniano.

Durante o Século XIX, os matemáticos comezaron a formalizar todos os diferentes ramos da matemática. Weierstrass defendía que se se construíse o cálculo infinitesimal sobre a Aritmética no canto de sobre a Xeometría, o que favorecía a definición de Euler en relación á de Leibniz (vexa aritmetización da análise). Máis para o final do século, os matemáticos comezaron a tentar formalizar toda a Matemática usando teoría de conxuntos, e conseguiron obter definicións de todos os obxectos matemáticos en termos do concepto de conxunto. Foi Dirichlet quen criou a definición "formal" de función moderna.

Na definición de Dirichlet, unha función é un caso especial dunha relación. A relación é un conxunto de pares ordenados, onde cada elemento do par pertence a un dos conxuntos relacionados (nas relacións non existen restricións en canto á lei de correspondencia entre os elementos dos conxuntos, xa que é costume que as funcións introduzan restricións). Na maioría dos casos de interese práctico, porén, as diferenzas entre as definicións moderna e de Euler son desprezábeis.

Definición formal

Considere dous conxuntos X e Y. Unha función f de X en Y:

f:X\rightarrow Y

relaciona a cada elemento x de X, cun único elemento y=f(x) de Y.

Outra maneira de dicir isto é afirmar que f é unha relación binaria entre os dous conxuntos tal que:

f é unívoca: se y = f(x) e z = f(x), entón y = z.
f é total: para todos x en X, existe un y en Y tal que y = f(x).

Se se atende á segunda condición, e non á primeira, temos unha función multivalorada (tamén se usa ás veces o termo función multívoca na mesma acepción).

Se se atende á primeira condición, e non á segunda, temos unha función parcial.

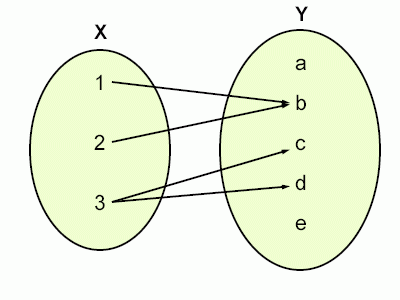
Considere as tres funcións seguintes:

	Esta non é unha función, pois o elemento 3 en X está asociado con dous elementos (b e c) en Y (a función non é funcional). Este é un exemplo de función multivalorada.
	Esta non é unha función, pois o elemento 1 en X non é asociado con ao menos un elemento en Y. Este é un exemplo de función parcial.
	Esta é unha función (no caso, unha función discreta). Esta pode definirse explicitamente pola expresión: $f(x)=\left\{{\begin{matrix}a,&{\mbox{se }}x=1\\c,&{\mbox{se }}x=2\\d,&{\mbox{se }}x=3.\end{matrix}}\right.$

Dominio, contradominio e imaxe

Son tres conxuntos especiais asociados á función. O dominio é o conxunto A do exemplo dado no inicio deste capítulo: contén todos os elementos x para os cales a función se debe definir. Xa o conxunto B do exemplo é o contradominio: o conxunto que contén os elementos poden ser relacionados a elementos do dominio.

Tamén se define o conxunto imaxe como o conxunto de valores que f(x) asume efectivamente. O conxunto imaxe é, pois, sempre un subconxunto do contradominio.

Funcións sobrexectivas , inxectivas e bixectivas

Artigo principal: Bixección,_inxección_e_sobrexección.

Os tipos de aplicacións poden clasificarse de acordo co seu comportamento con relación á regra unha única saída para cada entrada. Como non se dixo nada sobre as entradas, ou se as saídas teñen que ser únicas temos que resolver estas ambigüidades. Ao facer isto atopamos apenas tres tipos de clases de funcións (clase como en 'clasificación' non clases de equivalencia):

Funcións inxectoras (ou inxectivas), son funcións en que cada elemento do contra-dominio (da saída) esta asociado a apenas un elemento do dominio (da entrada), é dicir unha relación un para un entre os elementos do dominio e do contra-dominio. Isto é, cando $x\neq y$ no dominio (X) entón $f(x)\neq f(y)$ no contradominio (Y).

Funcións sobrexectoras (ou sobrexectiva), unha función en que todos os elementos do contra-dominio (da saída) están asociados a algún elemento do dominio (da entrada). Noutras palabras, iso significa que o conxunto imaxe é igual ao conxunto contra-dominio.

Funcións bixectoras (ou bixectiva), se fose á vez sobrexectora e inxectora, isto é, se todos os elementos do dominio están asociados un a un a todos os elementos do contra-dominio.

Notación

Existen varias formas estándar de denotar funcións. A notación máis usada é a notación funcional, que é a primeira notación que se describe a continuación.

Notación funcional

A notación funcional require que se lle dea un nome á función que, no caso dunha función inespecífica, adoita ser a letra $f$ . Entón, a aplicación da función a un argumento denotase polo seu nome seguido do seu argumento (ou, no caso dunha función multivariable, os seus argumentos) entre parénteses, como en

f(x),\quad \sin(3),\quad {\text{ou}}\quad f(x^{2}+1).

O argumento entre as parénteses pode ser unha variable, moitas veces $x$ , que representa un elemento arbitrario do dominio da función, un elemento específico do dominio ( $3$ no exemplo anterior), ou unha expresión que se pode avaliar a un elemento do dominio ( $x^{2}+1$ no exemplo anterior). O uso dunha variable non especificada entre parénteses é útil para definir unha función explicitamente como en "sexa $f(x)=\sin(x^{2}+1)$ ".

Cando o símbolo que denota a función consta de varios caracteres e non pode xurdir ambigüidade, é posible que se omitan os parénteses da notación funcional. Por exemplo, é común escribir $sin x$ en lugar de $sin(x)$ .

Utilízase habitualmente un tipo romano para as funcións con varias letras, como " $sin$ " para a función seno, en contraste coa fonte cursiva para símbolos dunha soa letra.

A notación funcional utilízase a miúdo de xeito coloquial para referirse a unha función e simultaneamente nomear o seu argumento, como en "sexa $f(x)$ unha función". Este é un abuso de notación que é útil para unha formulación máis sinxela.

Notación de frecha

A notación de frechas define a regra dunha función en liña, sen requirir que se lle dea un nome. Por exemplo, $x\mapsto x+1$ é a función que toma un número real como entrada e ten como saída ese número máis 1. De novo, un dominio e codominio de $\mathbb {R}$ está implícito.

O dominio e o codominio tamén se poden indicar explicitamente, por exemplo:

{\begin{aligned}\operatorname {sqr} :\mathbb {Z} &\rightarrow \mathbb {Z} \\x&\mapsto x^{2}.\end{aligned}}

Isto define unha función $sqr$ (elevar ao cadrado) desde os enteiros ata os enteiros que devolve o cadrado da súa entrada.

Como aplicación común da notación de frecha, supoña que $f:X\times X\to Y;\;(x,t)\mapsto f(x,t)$ é unha función en dúas variables, e queremos referirnos a unha función aplicada parcialmente $X\to Y$ producida fixando o segundo argumento ao valor $t 0$ sen introducir un novo nome de función. O mapa en cuestión pódese denotar $x\mapsto f(x,t_{0})$ usando a notación de frecha. A expresión $x\mapsto f(x,t_{0})$ (léase: "o mapa leva $x$ a $f$ de $x$ coma $t$ cero") representa esta nova función cun só argumento, mentres que a expresión $f (x 0, t 0)$ fai referencia ao valor da función $f$ no punto $(x 0, t 0)$ .

Notación de índice

Pódese usar a notación de índice en lugar da notación funcional. É dicir, en lugar de escribir $f (x)$ , escribe $f_{x}.$

Este é normalmente o caso de funcións cuxo dominio é o conxunto dos números naturais. Tal función chámase secuencia e, neste caso, o elemento $f_{n}$ chámase $n$ -ésimo elemento da secuencia.

A notación de índice tamén se pode usar para distinguir algunhas variables chamadas parámetros das "variables verdadeiras". De feito, os parámetros son variables específicas que se consideran fixas durante o estudo dun problema. Por exemplo, o mapa $x\mapsto f(x,t)$ (ver arriba) denotaríase $f_{t}$ usando a notación de índice, se definimos a colección de mapas $f_{t}$ pola fórmula $f_{t}(x)=f(x,t)$ para todo $x,t\in X$ .

Mapa

Unha función tamén se pode denominar mapa e usar o verbo mapear, mais algúns autores fan unha distinción entre o termo "mapa" e "función". Por exemplo, o termo "mapa" adoita reservarse para unha "función" con algún tipo de estrutura especial (por exemplo, mapa de variedades). En particular, pódese usar mapa en lugar de homomorfismo por motivos de concisión (por exemplo, mapa linear ou mapa de $G$ a $H$ en lugar de homomorfismo de grupo de $G$ a $H$ ).

Algúns autores, como Serge Lang, usan "función" só para referirse a mapas para os que o codominio é un subconxunto dos reais ou dos números complexos e usa o termo mapeamento para funcións máis xerais.

Na teoría dos sistemas dinámicos, un mapa denota unha función de evolución utilizada para crear sistemas dinámicos discretos. Ver tamén mapa de Poincaré.

Sexa cal sexa a definición de mapa que se use, termos relacionados como dominio, codominio, inxectiva, continua teñen o mesmo significado que para unha función.

Termo	Distinción de "función"
Mapa/Mapear	Ningúnha; os termos son sinónimos.^[1]
	Un mapa pode ter calquera conxunto como o seu codominio, mentres que, nalgúns contextos, normalmente en libros máis antigos, o codominio dunha función é especificamente o conxunto dos números reais ou complexos.^[2]
	Un mapa está asociado cunha estrutura especial (por exemplo, especificando explicitamente un codominio estruturado na súa definición). Por exemplo, un mapa linear.
Homomorfismo	Unha función entre dúas estruturas do mesmo tipo que conserva as operacións da estrutura (por exemplo, un homomorfismo de grupo).^[3]
Morfismo	Unha xeneralización de homomorfismos a calquera categoría, mesmo cando os obxectos da categoría non son conxuntos (por exemplo, un grupo define unha categoría cun só obxecto, que ten os elementos do grupo como morfismos.^[4]

Notas

↑ Weisstein, Eric W. "Map". mathworld.wolfram.com (en inglés). Consultado o 2019-06-12.
↑ Lang, Serge (1987). "III §1. Asignations". En Springer. Linear Algebra (3rd ed.). p. 43. ISBN 978-0-387-96412-6. Unha función é un tipo especial de asignación, é dicir, é unha asignación dun conxunto ao conxunto de números, é dicir, a R, ou a C ou a un campo K.
↑ James, Robert C.; James, Glenn (1992). Van Nostrand Reinhold, ed. Dicionario de matemáticas (5ª ed.). p. 202. ISBN 0-442-00741-8. OCLC 25409557.
↑ James & James 1992, p. 48

Véxase tamén

Bibliografía

Bartle, Robert (1976). The Elements of Real Analysis (2nd ed.). Wiley. ISBN 978-0-471-05465-8. OCLC 465115030.
Bloch, Ethan D. (2011). Proofs and Fundamentals: A First Course in Abstract Mathematics. Springer. ISBN 978-1-4419-7126-5.
Cunningham, Daniel W. (2016). Set theory: A First Course. Cambridge University Press. ISBN 978-1-107-12032-7.
Gödel, Kurt (1940). The Consistency of the Continuum Hypothesis. Princeton University Press. ISBN 978-0-691-07927-1.
Halmos, Paul R. (1970). Naive Set Theory. Springer-Verlag. ISBN 978-0-387-90092-6.
Jech, Thomas (2003). Set theory (3rd ed.). Springer-Verlag. ISBN 978-3-540-44085-7.
Spivak, Michael (2008). Calculus (4th ed.). Publish or Perish. ISBN 978-0-914098-91-1.

Outros artigos

[1] Weisstein, Eric W. "Map". mathworld.wolfram.com (en inglés). Consultado o 2019-06-12.

[Lang87p43-2] Lang, Serge (1987). "III §1. Asignations". En Springer. Linear Algebra (3rd ed.). p. 43. ISBN 978-0-387-96412-6. Unha función é un tipo especial de asignación, é dicir, é unha asignación dun conxunto ao conxunto de números, é dicir, a R, ou a C ou a un campo K.

[3] James, Robert C.; James, Glenn (1992). Van Nostrand Reinhold, ed. Dicionario de matemáticas (5ª ed.). p. 202. ISBN 0-442-00741-8. OCLC 25409557.

[4] James & James 1992, p. 48

[1]

[2]

[3]

[4]