Arco (xeometría)

Para outras páxinas con títulos homónimos véxase: Arco.

Arco dunha circunferencias.

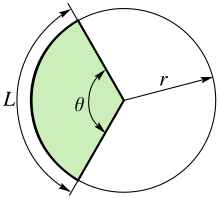
Na xeometría, arco é calquera curva continua que une dous puntos. Existen arco de circunferencia, de elipse, de parábola e outras figuras xeométricas.

O arco circunferencia fica definido por tres puntos, ou dous puntos extremos e o raio ou a corda da circunferencia. A corda une os dous extremos do arco, estando a frecha unindo os puntos medios.

Arco dun cuadrante (en vermello)

Cálculo da lonxitude dun arco (rectificación dunha curva)

Métodos históricos

Antigüidade

No longo da historia das matemáticas moitos grandes pensadores consideraron imposible calcular a lonxitude dun arco irregular. Arquimedes ideou un método por aproximación de rectángulos para calcular a área dun polígono curvilíneo mediante o método de exhaustión, aínda que poucos creron que era posible que unha curva tivese unha lonxitude medible como as da liñas rectas.

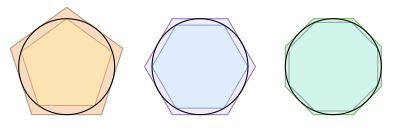
As primeiras medicións fixéronse a través de métodos de aproximación. Os matemáticos da época empezaron a trazar polígonos dentro da curva, e calculando a lonxitude dos lados destes, obtendo así a lonxitude aproximada da curva. Cantos máis segmentos se usasen, máis diminuía a lonxitude de cada segmento, e obtíñase unha aproximación cada vez mellor.

Método de exhaustión: cálculo da lonxitude da circunferencia mediante a aproximación de polígonos inscritos e circunscritos.

Século XVII

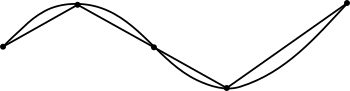
Nesta época, o método de esgotamento levou á rectificación por métodos xeométricos de moitas curvas transcendentais: a espiral logarítmica por Torricelli en 1645 (algúns pensan que foi John Wallis en 1650); o cicloide por Christopher Wren en 1658, e a catenaria por Gottfried Leibniz en 1691.

Determinar a lonxitude dun arco dun segmento irregular, facer a rectificación dunha curva, historicamente foi difícil. Aínda que foron utilizados varios métodos para curvas específicas, a chegada do cálculo trouxo consigo fórmulas xerais que daban solucións concretas para algúns casos.

A lonxitude dun arco de circunferencia de radio r e ángulo θ (medido en radiáns), con centro na orixe, é igual a θr. Para un ángulo α, medido en graos, a lonxitude en radiáns é α/180° × π, sendo a lonxitude de arco igual a (α/180°)πr.

Métodos modernos

Ao considerar unha función $f \left ( x \right )$ e a súa respectiva derivada $f' \left ( x \right )$, que son continuas nun intervalo [a, b], a lonxitude do arco delimitado por a e b vén dada pola fórmula:

$s = \int_{a}^{b} \sqrt{1 + \left [ f' \left ( x \right ) \right ] ^2} \, dx$

Se a función está definida parametricamente, onde $x = f \left ( t \right )$ e $y = g \left ( t \right )$:

$s = \int_{a}^{b} \sqrt{\left [ f' \left ( t \right ) \right ] ^2 + \left [ g' \left ( t \right ) \right ] ^2} \, dt$

Se a función está en coordenadas polares, onde a coordenada radial e o ángulo están relacionados $r = f (\theta)$, a lonxitude dunha curva redúcese a:

$s = \int_{a}^{b} \sqrt{r^2 + \left [ \frac {dr}{d \theta\ } \right ] ^2} \, d \theta\$

Na maioría dos casos non hai unha solución dispoñible e será necesario usar métodos de integración. Por exemplo, aplicar esta fórmula a unha elipse levaría a unha integral elíptica de segunda orde.

Entre as curvas con solucións coñecidas están a circunferencia, catenaria, cicloide, espiral logarítmica e parábola.

Lonxitude de arco

A lonxitude de arco é unha medida da lonxitude dun arco dunha curva calquera, se vén dada en coordenadas cartesianas, a lonxitude de arco pode calcularse como:

$L_a = \int_{x_1}^{x_2} \sqrt{1 + f'(x)^2}\ dx$

Se a curva vén especificada en coordenadas polares, a lonxitude entre o ángulo $\phi_1$ e $\phi_2$ vén dada por:

$L_a = \int_{\phi_1}^{\phi_2} \sqrt{\rho'(\phi)^2 + \rho(\phi)^2}\ d\phi$

Desta última dedúcese que para unha circunferencia, dado que $\scriptstyle \rho(\phi) = R$ e $\scriptstyle \rho'(\phi) = 0$, a lonxitude de arco pode expresarse simplemente como:

$L_a = R(\phi_2-\phi_1)\,$

Véxase tamén

Bibliografía

• Spiegel, Murray R.; Abellanas, Lorenzo (1992). Fórmulas y tablas de matemática aplicada. Aravaca (Madrid): McGraw-Hill. ISBN 84-7615-197-7. 

Ligazóns externas

• Arc, en mathworld