Cicloide

cicloide xerada por un círculo rodando.

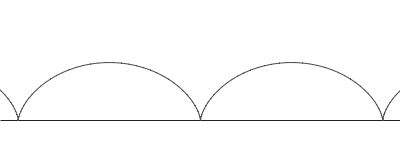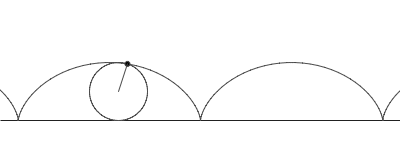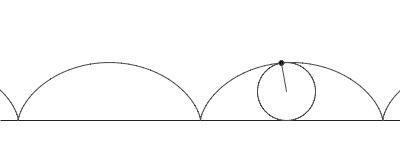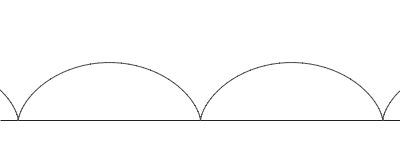
Unha cicloide é a curva definida polo camiño seguido por un punto na beira dunha circunferencia rodando ó longo dunha liña recta. É un exemplo dunha ruleta, unha curva xerada por unha curva rodando sobre outra.

A cicloide é ademais a solución ó problema da braquistócrona (i.e. a curva de descenso máis rápido entre dous puntos en diferente vertical baixo gravidade) e o problema relacionado co anterior da isócrona ou tautócrona (i.e. curva coa propiedade de que o tempo de descenso dun obxecto esvarando sen rozamento non depende da posición inicial na mesma).

Historia

A cicloide foi estudada en primeiro lugar por Nicolás de Cusa e despois por Marin Mersenne. Foi nomeada por Galileo no 1599. No 1634 G.P. de Roberval amosou que a área baixo unha cicloide é tres veces a área da súa circunferencia xeratriz. No 1658 Christopher Wren amosou que a lonxitude dunha cicloide é catro veces o diámetro da súa circunferencia xeratriz.

No 1696 o matemático Johann Bernoulli anunciou a solución ó problema da braquistócrona (a curva que proporciona o descenso máis rápido en condicións ideais cando existe gravidade, obxecto de estudo no cálculo de variacións), amosando que a solución era unha cicloide. Leibniz, Newton, Jacob Bernoulli e Guillaume de l'Hôpital, atoparon a solución do problema enunciado por Bernoulli. A cicloide emprégase para resolver o problema isócrono (proposto por Christiaan Huygens), no que, se desprezamos o rozamento e invertemos unha cicloide deixando deslizar un obxecto por ela, este chegará á parte máis baixa da curva nun intervalo de tempo que non depende do punto de partida.

Entre as demostracións sobre as súas propiedades atópanse as do matemático René Descartes, que obtivo mediante demostracións efectivas e elegantes a fórmula da recta tanxente nun punto calquera do arco da cicloide, empregando técnicas que despois desenvolvería como a xeometría diferencial.

A causa das continuas disputas entre os matemáticos do século XVII, ou polas propiedades de beleza da curva, a cicloide ten sido chamada "a Helena dos Xeómetras". No 1658 Blaise Pascal lanza un desafío ós matemáticos propoñendo determinar a lonxitude dun arco da cicloide, así como o seu centro de gravidade e a superficie do volume de revolución que xera a área plana que varre o arco de cicloide ó xirar, ben en torno ó eixo de abscisas, ou en torno ó de ordenadas, ou en torno ó eixo de simetría do arco de cicloide. Foron moitos os esforzos realizados no século XVII para tratar de comprender esta curva e as súas propiedades, tanto xeométricas como físicas, que teñen permitido desenvolver un gran número de aplicacións industriais.

Ecuacións

Unha cicloide xerada por unha circunferencia de radio r = 2.

A cicloide dende a orixe, xerada por un círculo de radio r, consiste no lugar xeométrico dos puntos (x, y) que cumpren

$x=r(t-\sin t)\,$

$y=r(1-\cos t)\,$

onde t é un parámetro real, correspondente ó ángulo rotado pola circunferencia xeratriz, medido en radiáns. Para un t dado, o centro da circunferencia sitúase en x = rt, y = r.

Resolvendo para t e substituíndo o seu valor, a ecuación cartesiana resulta

$x=r\cos ^{-1}\left(1-{\frac {y}{r}}\right)-{\sqrt {y(2r-y)}}$

O primeiro arco da cicloide constitúeno os puntos tales que

$0\leq t\leq 2\pi .\,$

A cicloide é diferenciable excepto nos vértices, os puntos nos que toca o eixo x, con derivada tendendo cara a $\infty$ ou $-\infty$ ó aproximarse a ditos puntos. O mapa dende t a (x, y) danos unha curva diferenciable ou paramétrica de clase C^∞ e a singularidade no que a derivada é 0 é un vértice ordinario.

A cicloide satisfai a ecuación diferencial

$\left({\frac {dy}{dx}}\right)^{2}={\frac {2r-y}{y}}.$

Área

Un arco de cicloide xerado por un círculo de radio r pode ser parametrizado por

$x=r(t-\sin t),\,$

$y=r(1-\cos t),\,$

con

$0\leq t\leq 2\pi .\,$

Como

${\frac {dx}{dt}}=r(1-\cos t),$

atopamos que a área baixo o arco é

${\begin{aligned}A&=\int _{t=0}^{t=2\pi }y\,dx=\int _{t=0}^{t=2\pi }r^{2}(1-\cos t)^{2}\,dt\\&=\left.r^{2}\left({\frac {3}{2}}t-2\sin t+{\frac {1}{2}}\cos t\sin t\right)\right|_{t=0}^{t=2\pi }\\&=3\pi r^{2}.\end{aligned}}$

Lonxitude do arco

A lonxitude dun arco S vén dada por

${\begin{aligned}S&=\int _{t=0}^{t=2\pi }\left(\left({\frac {dy}{dt}}\right)^{2}+\left({\frac {dx}{dt}}\right)^{2}\right)^{1/2}\,dt\\&=\int _{t=0}^{t=2\pi }2r\sin \left({\frac {t}{2}}\right)\,dt\\&=8r.\end{aligned}}$

Péndulo cicloide

Se a lonxitude dun péndulo é igual á da metade dunha cicloide, a masa suspendida dun péndulo pode percorrer asemade unha cicloide se o movemento lateral do fío de suspensión se ve limitado asemade por dúas metades de arcos de cicloide. Un péndulo tal é isócrono, non tendo desviación algunha o seu período ó variar a súa amplitude debido a que o camiño corresponde ó camiño isócrono ou tautócrono, unha das propiedades das cicloides.

Tipos de cicloides e Curvas relacionadas

Dependendo de onde se atope o punto P xerador da cicloide respecto da circunferencia xeratriz (Onde a circunferencia ten radio a, e a distancia do centro ó punto P é b), podemos distinguir:

• cicloide acurtada, se P atópase dentro da circunferencia xeratriz, (b < a),
• cicloide ('cicloide común'), se P pertence á circunferencia xeratriz, (a = b),
• cicloide alongada, se P está fóra da circunferencia xeratriz, (b > a).

Así, unha cicloide sería un conxunto de liñas particular dentro das trocoides.

Permitindo que a liña sobre a que roda a circunferencia sexa un círculo arbitrario, obtemos unha epicicloide (se a liña é trazada pola rodadura externa), unha hipocicloide (se a liña é trazada por rodadura interna), unha epitrocoide (epicicloide acurtada ou alongada), ou unha hipotrocoide (hipocicloide acurtada ou alongada).

Todas as curvas anteriores son ruletas, xeradas a partir dunha circunferencia rodando ó longo dunha liña de curvatura continua. As cicloides, epicicloides, e hipocicloides teñen a propiedade de ser cada unha semellante á súa evoluta. Se q é o produto da curvatura polo radio do círculo, con signo positivo para as epi- e negativo para as hipo-, entón a razón de semellanza curva:evoluta é 1 + 2q.

O espirógrafo clásico constrúe hipotrocoides e epitrocoides.

Uso en arquitectura

Arcos cicloides no Kimbell Art Museum.

O arco cicloide foi usado en diversas construcións, entre elas, polo arquitecto Louis Kahn no seu deseño do Museo de Arte Kimbell en Fort Worth (Texas), ou no Hopkins Center en Hanover (Nova Hampshire).

Véxase tamén

Ligazóns externas

• Ghatak, A. e Mahadevan, L.: "An application from physics", en Crack street: the cycloidal wake of a cylinder tearing through a sheet. Physical Review Letters, 91, (2003).
• Cicloides
• A Treatise on The Cycloid and all forms of Cycloidal Curves, monografía por Richard A. Proctor, B.A. en Cornell University Library.
• Cicloides e trocoides.
• Cycloid Curves por Sean Madsen con contribucións de David von Seggern.