Relatividade especial

A Teoría (Especial, Restrinxida ou Restrita) da Relatividade (tamén coñecida como relatividade especial, relatividade restrinxida ou RE), publicada pola primeira vez por Albert Einstein en 1905, describe a física do movemento en ausencia de campos gravitacionais.[1] Estes conceptos foron presentados anteriormente por Henri Poincaré e Hendrik Lorentz, que tamén son considerados iniciadores da teoría. Antes, a meirande parte dos físicos pensaban que a mecánica clásica de Isaac Newton, baseada na chamada relatividade de Galileo (orixe das ecuacións matemáticas coñecidas como transformacións de Galileo) describía os conceptos de velocidade e forza para todos os observadores (ou sistemas de referencia). Porén, Hendrik Lorentz e outros, comprobaran que as ecuacións de Maxwell, que gobernan o electromagnetismo, non se comportaban en acordo ás leis de Newton cando o sistema de referencia muda (por exemplo, cando se considera o mesmo problema físico dende o punto de vista de dous observadores que se moven un en relación ó outro). A noción de transformación das leis da física en respecto ós observadores é a que dá nome á teoría, que se axusta co cualificativo de especial ou restrinxida por cinxirse a casos de sistemas nos que non se teñen en conta campos gravitatorios. Unha extensión desta teoría é a Teoría Xeral da Relatividade, publicada igualmente por Einstein en 1916 e incluíndo os ditos campos.[2]
Motivación da teoría[editar | editar a fonte]
As leis de Newton consideran que tempo e espazo son os mesmos para os diferentes observadores dun mesmo fenómeno físico. Antes da formulación da teoría especial da relatividade, Hendrik Lorentz e outros tiñan descuberto que o electromagnetismo difería da física newtoniana en que as observacións dun fenómeno poderían diferir dunha persoa a outra que estivera movéndose en relación á primeira a velocidades próximas ás da luz. Así, unha pode observar a inexistencia dun campo magnético en canto a outra observa o dito campo no mesmo espazo físico.
Lorentz suxeriu unha teoría do éter na que obxectos e observadores viaxarían a través dun éter estacionario, sufrindo un acurtamento físico (hipótese de contracción de Lorentz) e unha mudanza no paso do tempo (dilatación do tempo). Isto subministraba unha reconciliación parcial entre a física newtoniana e o electromagnetismo, que se conxugaban aplicando a transformación de Lorentz, que viría a substituír a transformación de Galileo vixente no sistema newtoniano. Cando as velocidades involucradas son moito menores que c (velocidade da luz), as leis resultantes son na práctica as mesmas que na teoría de Newton, e as transformacións redúcense ás de Galileo. De calquera xeito, a teoría do éter foi criticada aínda polo mesmo Lorentz debido á súa natureza ad hoc.
Cando Lorentz suxeriu a súa transformación como unha descrición matemática precisa dos resultados dos experimentos, Einstein derivou as mesmas ecuacións de dúas hipóteses fundamentais: a constancia da velocidade da luz, c, e a necesidade de que as leis da física sexan iguais (invariantes en diferentes sistemas inerciais, quer dicir, para diferentes observadores. Desta idea xurdiu o título orixinal da teoría, “Teoría dos invariantes“. Foi Max Planck quen suxeriu despois o termo "relatividade" para resaltar a noción de transformación das leis da física entre observadores movéndose relativamente entre si.
A relatividade especial estuda o comportamento de obxectos e observadores que permanecen en repouso ou móvense con movemento uniforme (i.e., velocidade relativa constante). Neste caso, dise que o observador está nun sistema de referencia inercial. A comparación de espazos e tempos entre observadores inerciais pode ser realizada usando as transformacións de Lorentz. A teoría especial da relatividade pode predicir así mesmo o comportamento de corpos acelerados cando a devandita aceleración non implique forzas gravitacionais, caso no que é necesaria a relatividade xeral.
Campos magnéticos xerados pola corrente eléctrica[editar | editar a fonte]
A relación entre a electricidade e o magnetismo, baseada na capacidade da corrente eléctrica para desviar unha agulla magnética, foi descuberta de xeito independente por Gian Domenico Romagnosi e Hans Christian Ørsted. Ningún dos dous deron coas consecuencias nin desenvolveron ningunha teoría para explicalo. Romagosi descubriuno en 1802 e enviou un informe á Academia de París, pero naquel intre a comunidade científica ignórao.[3] En 1820, Hans Christian Ørsted redescubre o fenómeno e presenta o seu experimento en Xenebra. Francesc Aragó presenciou o experimento de Ørsted en Xenebra, repetiuno en París e animou a Ampère a investigar sobre o fenómeno.[4] Ampère deduciu que as accións magnéticas son producidas polo movemento da electricidade.
Este feito presenta un problema fundamental. Por unha banda se unha corrente eléctrica crea un campo magnético, unha carga eléctrica en movemento ten que crear un campo magnético. Mais se un observador se move conxuntamente coa carga, ora non observa ningún campo magnético (xa que para el a carga non se move), ora a lei do campo magnético inducido por unha corrente non é a mesma dependendo da velocidade do observador.
De feito, se dúas cargas eléctricas fican inmóbiles entre si e o observador, este só tería que observar a forza calculada segundo a lei da electrostática:

.
En troques, se as dúas cargas se moven conxuntamente a unha velocidade v respecto do observador, entón segundo as leis do campo magnético, ademais tería que observar unha forza magnética.
O campo magnético xerado pola segunda carga ó punto onde se atopa a primeira sería:
E a forza que este campo magnético faría sobre a primeira carga:
Polo tanto agora a forza total que se observaría entre as dúas cargas sería:
Mais iso é independente de se a velocidade relativa entre as cargas e o observador se produciu porque as cargas puxéronse en movemento ou porque se acelerou o observador. Un observador pode comezar o experimento medindo a forza entre dúas cargas en repouso en terra, subir a un vagón de tren e poñer en marcha o tren, ver como a forza entre as cargas varía.
A forza magnética comparada coa forza electrostática é extraordinariamente pequena:
Onde v é a velocidade relativa entre as cargas e o observador e α é o ángulo entre o vector que vai dunha carga á outra e o vector velocidade.
Tendo en conta que:
Resulta que o coeficiente que multiplica a velocidade é:
Para que esta forza sexa apreciable cómpre que, ou ben a velocidade sexa moi grande, ou ben que as forzas electrostáticas sexan moi grandes e se cancelen de xeito que só se aprecie a forza magnética. Isto é o que pasa no caso de fíos condutores da corrente, os fíos teñen cargas positivas e negativas que cancelan as forzas electrotáticas e só quedan as forzas magnéticas entre os portadores en movemento respecto do observador.
O experimento de Francesc Aragó de 1810[editar | editar a fonte]

En 1810, Francesc Aragó fai un experimento, que presenta oralmente na Academia de Ciencias o 10 de decembro (malia que non se publicou até 1853 xusto antes da súa morte, máis de corenta anos máis tarde): tratábase de medir a velocidade da luz que ve das estrelas, comparando o valor pola mañá ás 6 h e polo serán ás 18 h. Ás 6 h, cando se observa un estrela no cénit, a Terra achégase á estrela, teríase que medir c + V, onde V é a velocidade tanxencial de rotación da Terra e c a velocidade da luz; ás 18 h, para unha estrelo no cénit, a Terra afástase, teríase que medir c - V. Agora ben, a experiencia resultou negativa. As diferenzas observadas foron moi pequenas, da mesma orde de magnitude que as observadas entre diferentes estrelas e perfectamente atribuíbles a erros de experimentación. En outubro, Aragó repetiu o experimente e o resultado volve ser o mesmo. A velocidade de rotación da terra arredor do sol tampouco afectou a velocidade observada da luz.[5]
Neste experimento, Aragó non mide directamente a velocidade da luz senón que o fai indirectamente a partir do índice de refracción. Isto fai que haxa unha posible explicación que permita conciliar este resultado coas leis de Newton, Aragó di:
Semella que non se pode dar razón máis que supoñendo que os corpos luminosos emiten raios con toda clase de velocidades, coa condición de que se admita igualmente que estes raios non son visibles máis que cando as súas velocidades están comprendidas entre uns límites determinados: baixo estas hipéteses, en efecto, a visibilidade dos raios dependerá das súas velocidades relativas e, como estas velocidades determinan a cantidade de refracción, os raios visibles serán sempre igualmente refractadosFrancesc Aragó
O único xeito de resolver a cuestión era a medida directa da velocidade da luz. Aragó definiu os principios xerais do sistema para medir directamente a velocidade da luz pero os seus problemas de visión impedíronlle participar nos experimentos.
Finalmente Fizeau mediu directamente en 1849,[6] máis tarde Léon Foucault en 1862[7] e Albert Abraham Michelson en 1878[8]
As medidas experimentais tiñan cada vez máis precisión e sempre daban o mesmo resultado do experimento de Aragó de 1810: A velocidade da luz era constante e independente da velocidade relativa entre o emisor e o receptor.
Invarianza da velocidade da luz[editar | editar a fonte]
Para fundamentar a RE, Einstein postulou que a velocidade da luz no baleiro é a mesma para todos os observadores inerciais.[9][10] De igual xeito, resaltou que toda a teoría física debe ser descrita por leis que teñan forma matemática semellante en calquera sistema de referencia inercial. O primeiro postulado está en concordancia coas ecuacións de Maxwell do electromagnetismo, e o segundo usa un principio de razoamento lóxico, do xeito do principio antrópico.
Einstein amosou que dos ditos principios dedúcense as ecuacións de Lorentz, e, ó aplicalas baixo estes conceptos, a mecánica resultante ten varias propiedades interesantes:
- Cando as velocidades dos obxectos considerados son moito menores que a velocidade da luz, as leis resultantes son as descritas por Newton.
De igual xeito, o electromagnetismo non é xa un conxunto de leis que necesite unha transformación diferente da aplicada en mecánica.
- O tempo e o espazo deixan de ser invariantes ó mudar de sistema de referencia, pasando a ser dependente das velocidades relativas dos sistemas de referencia dos observadores: Dous eventos que ocorren de xeito simultáneo en diferentes lugares para un sistema de referencia, poden ocorrer en tempos diferentes noutro sistema de referencia (a simultaneidade é relativa). De igual xeito, se ocorren nun mesmo lugar nun sistema, poden ocorrer en lugares diferentes noutro.
- Os intervalos temporais entre sucesos dependen do sistema de referencia no que se miden (por exemplo, o célebre paradoxo dos xemelgos). As distancias entre sucesos, tamén.
As dúas primeiras propiedades resultaban atractivas, pois calquera teoría nova debe explicar as observacións xa existentes, e estas indicaban que as leis de Newton eran moi precisas. A terceira conclusión foi inicialmente moi discutida, pois tiraba por terra moitos conceptos ben coñecidos e aparentemente obvios, como o concepto de simultaneidade.

Inexistencia dun sistema de referencia absoluto[editar | editar a fonte]
Outra consecuencia é o rexeito da noción dun único e absoluto sistema de referencia. Antes críase que o universo viaxaba a través dunha substancia coñecida como éter (identificable como o espazo absoluto) en relación á que podían ser medidas velocidades. Porén, os resultados de varios experimentos, que culminaron no famoso experimento de Michelson-Morley, suxeriron que, ben a Terra estaba sempre estacionaria (o que é un absurdo), ben a noción dun sistema de referencia absoluto era errónea e debía de ser rexeitada. Einstein concluíu coa teoría especial da relatividade que calquera movemento é relativo, non existindo ningún concepto universal de "estacionario".
Equivalencia de masa e enerxía[editar | editar a fonte]
Pero pode ser que moito máis importante foi a demostración de que enerxía e masa, antes consideradas propiedades medibles diferenciadas, eran equivalentes, e relacionábanse a través da que é, sen dúbida, a ecuación máis famosa da teoría:
onde E é a enerxía, m é a masa e c é a velocidade da luz no baleiro. Se o corpo estase movendo á velocidade v relativa ó observador, a enerxía total do corpo é:
- E = γ·m·c2,
O γ é frecuente en relatividade. Derívase das ecuacións de transformación de Lorentz. Cando v é moito menor que c pódese usar unha aproximación de γ (obtida polo desenvolvemento en serie de Taylor), igual á enerxía en repouso, mc2, máis a enerxía cinética newtoniana, ½mv2. Este é un exemplo de como as dúas teorías coinciden cando as velocidades son pequenas.
Ademais, á velocidade da luz, a enerxía será infinita, o que impide que as partículas que teñen masa en repouso poidan acadar a velocidade da luz.
A implicación máis práctica da teoría é que pon un límite superior ás leis (ver Lei da natureza) da Mecánica clásica e a gravidade propostas por Isaac Newton cando as velocidades se achega á da luz. Nada que poida transportar masa ou información pode moverse máis rápido ca a devandita velocidade. Cando un obxecto se achega á velocidade da luz (en calquera sistema) a cantidade de enerxía requirida para seguir aumentando a súa velocidade aumenta de xeito rápido e sintótico cara ó infinito, facendo imposible acadar a velocidade da luz. Só partículas sen masa, como os fotóns, poden acadar esa velocidade (e ademais deben trasladarse en calquera sistema de referencia a esa velocidade) que é aproximadamente 300000 quilómetros por segundo (3·108 ms−1).
O nome taquión foi usado para nomear partículas hipotéticas que se poderían mover máis rápido ca a velocidade da luz. Na actualidade, aínda non hai evidencia experimental da súa existencia.
A relatividade especial tamén amosa que o concepto de simultaneidade é relativo ó observador: Se a materia pode viaxar ó longo dunha liña (traxectoria) no espazo-tempo sen mudar de velocidade, a teoría chama a esta liña intervalo temporal, pois un observador, seguíndoa, non podería sentir movemento (estaría en repouso), senón tan só viaxar no tempo en acordo ó seu sistema de referencia. De xeito semellante, un intervalo espacial significa unha liña recta no espazo-tempo ó longo da que nin a luz nin outra sinal máis lenta podería viaxar. Sucesos ó longo dun intervalo espacial non poden influenciarse un ó outro transmitindo luz ou materia, e poden aparecer como simultáneos a un observador nun sistema de referencia adecuado. Para observadores en diferentes sistemas de referencia, o suceso A pode parecer anterior ó B ou viceversa. Isto non sucede cando consideramos sucesos separados por intervalos temporais.
A Relatividade Especial é universalmente aceptada pola comunidade física na actualidade, ó contrario da Relatividade Xeral que está confirmada, pero con experiencias que poderían non excluír algunha teoría alternativa da gravitación. Porén, hai aínda un conxunto de xente oposta á RE en varios campos, téndose proposto varias alternativas, como as chamadas Teorías do Éter.
A teoría[editar | editar a fonte]
A RE usa tensores ou cuadrivectores para definir un espazo non-euclídeo. Este espazo, porén, é semellante en moitos aspectos e doado de traballar con el. A diferencial da distancia (ds) nun espazo euclídeo ven definida como:
- ds2=dx12+dx22+dx32
onde dx1, dx2, dx3 son diferenciais das tres dimensións espaciais. Na xeometría da relatividade especial, unha carta dimensión, o tempo, foi engadida, pero é tratada como unha cantidade imaxinaria con unidades de c, ficando a ecuación para a distancia, en forma diferencial, como:
- ds2=dx12+dx22+dx32-c2dt2
Se reducimos as dimensións espaciais a 2, podemos facer unha representación física nun espazo tridimensional,
- ds2=dx12+dx22-c2dt2
Podemos ver que as xeodésicas con medida cero forman un cono dual.

definido pola ecuación
- ds2=0=dx12+dx22-c2dt2
, ou
- dx12+dx22=c2dt2
A anterior ecuación é a do círculo con r=c*dt. Se estendemos o anterior ás tres dimensións espaciais, as xeodésicas nulas son esferas concéntricas, con raio =distancia= c*(+ o -)tempo. 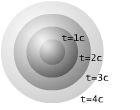
- ds2=0=dx12+dx22+dx32-c2dt2
- dx12+dx22+dx32=c2dt2
Este duplo cono de distancias nulas representa o "horizonte de visión" dun punto no espazo. Isto é, cando miramos ás estrelas e dicimos "A estrela da que estou recibindo luz ten X anos.", estamos vendo a través desa liña de visión: unha xeodésica de distancia nula. Estamos vendo un suceso a d=√{x12+x22+x32} metros, e d/c segundos no pasado. Por esta razón o duplo cono é tamén coñecido como cono de luz. O punto inferior da esquerda do diagrama inferior representa a estrela, a orixe representa o observador e a liña representa a xeodésica nula, o "horizonte de visión" ou cono de luz.

Xeometricamente, todos os "pintos" ó longo do cono de luz dan información (representan) o mesmo punto no espazo-tempo (a causa de que a distancia entre eles é 0). Isto pode ser pensado como 'un punto de neutralización' de forzas. ("A conexión prodúcese cando dous movementos, cada un deles excluínte do outro, xúntanse nun momento." - cita de James Morrison) É onde os sucesos no espazo-tempo intersectan, onde o espazo interactúa consigo mesmo. É como un punto ve o resto do universo e é visto. O cono na rexión -t inclúe a información que o punto recibe, mentres a rexión +t do cono engloba a información que o punto envía. Desta forma, o que podemos visionar é un espazo de horizontes de visión, e recaer no concepto de autómata celular, aplicándoo nunha secuencia continua espazo-temporal. Isto tamén conta para puntos en movemento uniforme de translación relativo sistemas inerciais.
Isto significa que a xeometría do universo permanece a mesma sexa cal sexa a velocidade(δx/δ t) (inercial) do observador. Así recaemos na lei de movemento de Newton: un obxecto en movemento tende a permanecer en movemento; un obxecto en repouso tende a permanecer en repouso.
Lei de conservación da enerxía cinética[editar | editar a fonte]
Con todo, a xeometría non permanece constante cando hai implicada aceleración (δx2/δ t2) , o que comporta unha aplicación de forza (F=ma), e en consecuencia unha mudanza en enerxía, o que nos leva á relatividade xeral, na que a curvatura intrínseca do espazo-tempo é directamente proporcional á densidade de enerxía no dito punto.
Modificacións da relatividade especial[editar | editar a fonte]
A comezos do século XXI foron postuladas un certo número de versións modificadas da RE.
Tests de postulados da relatividade especial[editar | editar a fonte]
- Experimento Michelson-Morley – arrastre do éter
- Experimento Hamar – obstrución do fluxo do éter
- Experimento Trouton-Noble - torque nun condensador
- Experimento Kennedy-Thorndike – contracción do tempo
- Experimento sobre as formas de emisión
Notas[editar | editar a fonte]
- ↑ Albert Einstein (1905) "Zur Elektrodynamik bewegter Körper", Annalen der Physik 17: 891
- ↑ Tom Roberts and Siegmar Schleif (outubro de 2007). Usenet Physics FAQ, ed. "What is the experimental basis of Special Relativity?". Consultado o 7 de setembro de 2008.
- ↑ "Romagnosi fisico". Arquivado dende o orixinal o 05 de decembro de 2008. Consultado o 22 de xaneiro de 2016.
- ↑ Iniciación á física. Julian Fernandez Ferrer y Marcos Pujal Carrera, Tomo II páxina 108 ISBN 84-400-6771-2
- ↑ Mémoire sur la vitesse de la lumière Memoria lida por Aragó na Academia das Ciencias en 1810 e publicada en 1853.
- ↑ Fizeau, H. L., «Sur une experience relative a la vitesse de propogation de la lumiere», Comptes Rendus 29, 90-92, 132, 1849
- ↑ Foucault, J. L., «Determination experimentale de la vitesse de la lumiere: parallaxe du Soleil», a Comptes Rendus 55, 501-503, 792-796, 1862
- ↑ Michelson, A. A., «Experimental Determination of the Velocity of Light», Proceedings of the American Association for the Advancement of Science 27, 71-77, 1878
- ↑ Albert Einstein (2001). Routledge, ed. Relativity: The Special and the General Theory (Reprint of 1920 translation by Robert W. Lawson ed.). p. 48. ISBN 0-415-25384-5.
- ↑ Richard Phillips Feynman (1998). Basic Books, ed. Six Not-so-easy Pieces: Einstein's relativity, symmetry, and space–time (PDF). p. 68. ISBN 0-201-32842-9. Consultado o 4 de marzo de 2023.[Ligazón morta]
Véxase tamén[editar | editar a fonte]
| Wikimedia Commons ten máis contidos multimedia na categoría: Relatividade especial |
Bibliografía[editar | editar a fonte]
- Einstein, Albert (2017). Verbo da teoría da relatividade restrinxida e xeral. Consello da Cultura Galega.
- Einstein, Albert (1996). The Meaning of Relativity. Fine Communications. ISBN 1-56731-136-9
- Logunov, Anatoly A. (2005) Henri Poincaré and the Relativity Theory (transl. from Russian by G. Pontocorvo e V. O. Soleviev, editado por V. A. Petrov) Nauka, Moscova.
- Charles Misner, Kip Thorne, e John Archibald Wheeler (1971) Gravitation. W. H. Freeman & Co. ISBN 0-7167-0334-3
- Post, E.J., 1997 (1962) Formal Structure of Electromagnetics: General Covariance and Electromagnetics. Dover Publications.
- Wolfgang Rindler (1991). Introduction to Special Relativity (2nd ed.), Oxford University Press. ISBN 978-0-19-853952-0; ISBN 0-19-853952-5
- Harvey R. Brown (2005). Physical relativity: space–time structure from a dynamical perspective, Oxford University Press, ISBN 0-19-927583-1; ISBN 978-0-19-927583-0
- Qadir, Asghar (1989). World Scientific Publications, ed. Relativity: An Introduction to the Special Theory. Singapur. p. 128. ISBN 9971-5-0612-2.
- Silberstein, Ludwik (1914) The Theory of Relativity.
- Lawrence Sklar (1977). University of California Press, ed. Space, Time and Spacetime. ISBN 0-520-03174-1.
- Lawrence Sklar (1992). Westview Press, ed. Philosophy of Physics. ISBN 0-8133-0625-6.
- Taylor, Edwin, e John Archibald Wheeler (1992) Spacetime Physics (2nd ed.). W.H. Freeman & Co. ISBN 0-7167-2327-1
- Tipler, Paul, e Llewellyn, Ralph (2002). Modern Physics (4th ed.). W. H. Freeman & Co. ISBN 0-7167-4345-0
Outros artigos[editar | editar a fonte]
Ligazóns externas[editar | editar a fonte]
Atención: Este artigo ou apartado precisa dun traballo de revisión. Por favor, vexa a lista de problemas indicados neste modelo e de acordo coas indicacións. Cando os problemas se resolvan, retire esta mensaxe, pero non quite esta mensaxe ata que estea todo solucionado. De ser posible, sería mellor substituír este marcador por outro máis específico. (Desde xaneiro de 2017) |
- Traballos orixinais
- Zur Elektrodynamik bewegter Körper traballo orixinal de Einstein en alemán, Annalen der Physik, Berna 1905
- On the Electrodynamics of Moving Bodies tradución inglesa publicada en 1923 no libro The Principle of Relativity.
- Visualización
- Raytracing Special Relativity Software visualizing several scenarios under the influence of special relativity.
- Real Time Relativity Arquivado 08 de maio de 2013 en Wayback Machine. The Australian National University. Relativistic visual effects experienced through an interactive program.
- Spacetime travel A variety of visualizations of relativistic effects, from relativistic motion to black holes.
- Through Einstein's Eyes Arquivado 14 de maio de 2013 en Wayback Machine. The Australian National University. Relativistic visual effects explained with movies and images.
- Warp Special Relativity Simulator A computer program to show the effects of traveling close to the speed of light.
- Animation clip no YouTube visualizing the Lorentz transformation.
- Original interactive FLASH Animations from John de Pillis illustrating Lorentz and Galilean frames, Train and Tunnel Paradox, the Twin Paradox, Wave Propagation, Clock Synchronization, etc.
- Relativistic Optics at the ANU
- lightspeed An OpenGL-based program developed to illustrate the effects of special relativity on the appearance of moving objects.
- Animation showing the stars near Earth, as seen from a spacecraft accelerating rapidly to light speed.







