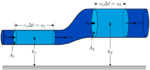
Ecuacións de Navier-Stokes
Este artigo contén varias ligazóns externas e/ou bibliografía ao fin da páxina, mais poucas ou ningunha referencia no corpo do texto. Por favor, mellora o artigo introducindo notas ao pé, citando as fontes. Podes ver exemplos de como se fai nestes artigos. |
As ecuacións de Navier-Stokes son un conxunto de ecuacións diferenciais que describen o escoamento de fluídos. Son ecuacións de derivadas parciais que permiten determinar os campos de velocidade e de presión.
Son de grande interese nun sentido puramente matemático. A pesar da súa gran variedade de usos prácticos, aínda non se comprobou se as solucións sempre existen en tres dimensións e, se existen, se son suaves, é dicir, son infinitamente diferenciables en todos os puntos do dominio. Son os chamadaos problemas de existencia e suavidade de Navier-Stokes. O Instituto de Matemáticas Clay incluíu este problema entre os sete problemas abertos máis importantes en matemáticas e ofreceu un premio de 1 millón de dólares por unha solución ou contraexemplo.[1]
Introdución[editar | editar a fonte]
As ecuacións de Navier-Stokes foron denominadas así despois de que Claude-Louis Navier e George Gabriel Stokes desenvolvesen un conxunto de ecuacións que describirían o movemento das substancias fluídas tales como líquidos e gases. Estas ecuacións estabelecen que os cambios no momento e aceleración dunha partícula fluída son simplemente o produto (resultado) dos cambios na presión e forzas viscosas disipativas (similar á fricción) actuando dentro do fluído. Esta forza viscosa orixínase na interacción molecular. Por tanto, son un dos máis útiles conxuntos de ecuacións porque describen a física dun gran número de fenómenos de interese económico e académico. Son usadas para crear modelos de clima, correntes oceánicas, fluxos da auga en canos, movementos das estrelas dentro da galaxia, fluxo ao redor de aerofolios (asas), propagación de fume en incendios etc. Tamén son usadas nos proxectos de aeronaves e coches, o estudo do fluxo sanguíneo, proxectos de centrais hidroeléctricas, análise dos efectos da polución etc. Xuntamente coas ecuacións de Maxwell, poden ser usadas para a modelaxe en estudos na magnetodinámica.
As ecuacións de Navier-Stokes son ecuacións diferenciais que describen o movemento dun fluído. Estas ecuacións, diferentes das ecuacións alxébricas, non procuran estabelecer unha relación entre as variábeis de interese (por exemplo velocidade e presión). En vez disto, estabelecen relacións entre as taxas de variación ou fluxos destas cantidades. En termos matemáticos, estas razóns corresponden ás súas derivadas. As ecuacións de Navier-Stokes para o caso máis simple dun fluído ideal con viscosidade cero, estabelecen que a aceleración (a razón de variación da velocidade) é proporcional á derivada da presión interna.
Isto significa que as solucións das ecuacións de Navier-Stokes para un problema físico dado deben ser obtidas coa axuda do cálculo. En termos prácticos, só os casos máis simples poden ser resoltos desta forma e as súas solucións exactas son coñecidas. Estes casos frecuentemente envolven fluxo non-turbulento en estado estacionario (o fluxo non varía como o tempo) no cal a viscosidade do fluído é grande ou a súa velocidade pequena (número de Reynolds pequeno).
Para situacións máis complexas, tales como un sistema de clima global como El Niño ou a sustentación nunha asa, as solucións para a ecuación de Navier-Stokes frecuentemente deben ser encontradas coa axuda de computadoras. Este é un campo da ciencia coñecido como CFD, sigla do inglés Computational Fluid Dynamics ou Dinámica dos Fluídos Computacional.
Aínda que a turbulencia sexa un fenómeno de nosa experiencia diaria, é extremadamente difícil encontrar solucións para esta clase de problemas. Un premio de 1 000 000 U$ foi ofrecido en maio de 2000 polo Instituto de Matemática Clay para calquera persoa que fixese progresos substanciais na dirección dunha matemática teórica que poida axudar a entender este fenómeno.
Suposicións básicas[editar | editar a fonte]
Antes de entrar nos detalles da ecuación de Navier-Stokes, é necesario facer varias suposicións sobre os fluídos. A primeira é que un fluído é un medio continuo, o que significa que non contén baleiros —como por exemplo, burbullas disoltas no gas— ou que non consiste en partículas como a borraxeira. Outra hipótese necesaria é que todas as variábeis de interese tales como presión, velocidade, densidade, temperatura etc., son diferenciábeis (isto é, non ten transición de fase).
Estas ecuacións son obtidas de principios básicos de conservación da masa, momento e enerxía. Para este obxectivo, algunhas veces é necesario considerar un volume arbitrariamente finito, chamado volume de control, sobre o cal estes principios poidan ser facilmente aplicados. Este volume é representado por e a súa superficie de confinamento por . O volume de control permanece fixo no espazo ou pode moverse como o fluído. Isto conduce, con todo, a consideracións especiais, como se mostrará a seguir.
A derivada material[editar | editar a fonte]
Os cambios nas propiedades dun fluído en movemento poden ser medidos de dúas formas diferentes. Iso será ilustrado a través dun exemplo, utilizando a medición da velocidade do vento na atmosfera. Unha forma de medir estas mudanzas é coa axuda do anemómetro nunha estación climática, ou pola liberación dun balón atmosférico. Claro que o primeiro caso é máis indicado para a medición da velocidade de todas as partículas que pasan a través dun punto fixo no espazo. No segundo caso, o instrumento está medindo mudanzas na velocidade a medida que se move co fluído. A mesma situación xorde con medidas da mudanza da densidade, temperatura etc. Cando aplicamos unha diferenciación debemos destacar as diferenzas destes dous casos. A derivada dun campo con respecto a unha posición fixa no espazo é coñecida como espacial ou derivada de Euler. A derivación acompañando o movemento dunha partícula é chamada substantiva ou derivada langraxiana.
A derivada material é definida polo operador:
onde é a velocidade do fluído. O primeiro termo do lado dereito da ecuación é a derivada tradicional de Euler (isto é, a derivada con referencia a un punto fixo); o segundo termo representa os cambios provocados polo movemento do fluído.
Leis de conservación[editar | editar a fonte]
As ecuacións de Navier-Stokes son derivadas dos principios da conservación da:
Adicionalmente, é necesario asumir unha relación constitutiva ou ecuación de estado para o fluído.
Na súa forma máis xeral, unha lei de conservación estabelece que a razón de cambio dunha propiedade continua , definida en todo volume de control, debe ser igual a aquilo que se perde a través das fronteiras do volume, cargado para fóra polo movemento do fluído, mais o que é creado/consumido polas fontes e sorbedoiros dentro do volume de control. Isto exprésase pola ecuación integral:
Onde v é a velocidade do fluído e representa as fontes e sorbedoiros no fluído.
Se o volume de control é fixado no espazo entón a ecuación integral pode ser expresada así:
Nótese que o teorema da diverxencia de Gauss foi usado na dedución desta última ecuación, de forma a expresar o primeiro termo do lado dereito no interior do volume de control. Por tanto:
Esta expresión é válida para , que é un volume de control que permanece fixo no espazo. Debido a que non varía no tempo, é posíbel trocar os operadores "" e "". E como esta expresión é valida para todos os dominios podemos, alén diso, remover a integral.
Coa introdución da derivada material obtemos, cando (ningunha fonte ou sorbedoiro):
Ecuación da continuidade[editar | editar a fonte]
A conservación da masa é descrita así:
onde é a densidade de masa (masa por unidade de volume), e v é a velocidade do fluído.
No caso dun fluído incompresíbel, non é unha función do tempo ou espazo e a ecuación redúcese a:
Conservación do momento[editar | editar a fonte]
A conservación do momento é expresa de maneira similar á ecuación de continuidade, co compoñente vector do momento substituíndo o de densidade, e cun termo fonte para representar as forzas que actúan no fluído.
Substituímos na ecuación de continuidade co momento rede por unidade de volume ao longo dunha dirección en particular, , onde é o compoñente da velocidade, isto é, a velocidade ao longo das direccións x, y ou z.
é a compoñente da forza actuando no fluído (sempre forza por unidade de volume). As forzas comunmente encontradas inclúen a gravidade e gradientes de presión. Isto tamén pode ser expresado como:
Nótese que é un tensor, o representa o produto tensorial.
Podemos simplificar isto máis, usando a ecuación de continuidade, obtendo:
que é frecuentemente escrita como:
Onde recoñecemos o usual F=ma.
A ecuación[editar | editar a fonte]
Forma xeral[editar | editar a fonte]
A forma das ecuacións[editar | editar a fonte]
A forma xeral das ecuacións de Navier-Stokes para a conservación do momento é:
onde é a densidade do fluído, v é o vector velocidade, e f é o vector de forza do corpo. O tensor representa as forzas superficiais aplicadas na partícula fluída (o tensor tensión). A menos que o fluído posúa un grao de liberdade de rotación, tal como nun vórtice, é un tensor simétrico. En xeral, temos a forma:
onde os son a tensión normal, a tensión tanxencial (tensión de cisallamento), e p é a presión estática, asociada como a parte isotrópica do tensor de tensións sen considerar se o fluído está ou non en equilibrio.
Finalmente, temos:
onde é a sumatoria da diagonal principal de .
Esta ecuación está aínda incompleta. Para completala, debe facerse unha hipótese en forma de , que é unha necesaria lei constitutiva para o tensor de tensións como se mostra abaixo.
O fluxo é tido como sendo diferenciábel e continuo, permitindo que as leis de conservación sexan expresas como ecuacións diferenciais parciais. No caso de fluídos incompresíbeis (densidade constante), as variábeis a seren seleccionadas son os compoñentes da presión e velocidade. Os tres compoñentes das ecuacións de Navier-Stokes mais a conservación da masa (ecuación de continuidade) forman un sistema fechado de ecuacións diferenciais parciais ben definidas para estas variábeis, que pode ser resolto, en principio, para condicións de contorno adecuadas.
A ecuación pode ser convertida para ecuacións de Wilkinson polo uso de variábeis secundarias vorticidade e función de fluxo. A solución depende das propiedades do fluxo (tales como viscosidade, calor específico, e condutividade térmica), e das solucións de contorno do dominio de estudo.
Ecuacións[editar | editar a fonte]
A forma xeral das ecuacións de Navier-Stokes é:
A interpretación desta ecuación vectorial (realmente tres ecuacións, unha para cada dimensión) é que a variación da cantidade de movemento dunha partícula fluída ou un volume de control é igual á suma do gradiente de presións, o tensor de tensións e as forzas aplicadas.
Formas especiais[editar | editar a fonte]
Estas son algunhas simplificacións usuais do problema para as cales algunhas solucións son coñecidas.
Fluídos Newtonianos[editar | editar a fonte]
Nos fluídos Newtonianos as seguintes hipóteses son válidas:
onde:
- é a viscosidade do fluído.
- é o delta Kronecker (1 para i=x; 0 se i x).
Para entender como isto foi derivado, notemos primeiro que no equilibrio, pix=-pδix. Para un fluído newtoniano, a variación do tensor forza covariante do valor de equilibrio é lineal no gradiente da velocidade. Obviamente non pode depender da propia velocidade debido á Covariancia de Galileo. Noutras palabras, pix+pδix é lineal na . Os fluídos que son considerados aquí son invariantes rotacionalmente (isto é, non son cristais líquidos).
Fluídos Binghan[editar | editar a fonte]
Nos fluídos de Binghan, temos algo lixeiramente diferente:
Estes son fluídos capaces de soportar algunha forza de cisallamento antes de iniciar o fluxo. Algúns exemplos comúns son a pasta de dentes ou a masa de modelaxe.
Fluídos incompresíbeis[editar | editar a fonte]
A meirande parte dos usos das ecuacións é en fluxos que se poden considerar incompresíbeis, isto non só se limita a fluídos incompresíbeis (líquidos) senón tamén a gases en fluxos con números de Mach inferiores a 0.3, onde o efecto da compresión é desprezábel. Se asumimos fluxo incompresíbel e viscosidade constante:
f representa "outras" forzas volumétricas (forzas por unidade de volume).
Explicando cada termo:
As ecuacións de Navier-Stokes separadas son
Para conservación de momento e
para conservación de masa.
onde
- é a densidade,
- () son os tres compoñentes da velocidade,
- forzas que actúan no corpo (tales como a gravidade),
- a presión,
- a viscosidade dinámica, dun punto do fluído;
- ;
- é a diverxencia,
- é o delta Kronecker.
Se é constante en todo o fluído, o momento da ecuación anterior é simplificado a
Se agora adicionalmente é asumido constante obtemos o seguinte sistema:
Ecuación de continuidade (asumindo incompresibilidade):
Nótese que as ecuacións de Navier-Stokes só poden describir o fluxo dun fluído aproximadamente. A unha escala extremamente pequena ou baixo condicións extremas, os fluídos reais están constituídos por unha mestura de moléculas discretas e outros materiais, tales como partículas en suspensión e gases disoltos, o que vai producir resultados diferentes dos obtidos dun fluído continuo e homoxéneo modelado pola ecuacións de Navier-Stokes. Dependendo do número Knudsen do problema, a mecánica estatística debe ser unha abordaxe máis apropiada. Con todo, as ecuacións de Navier-Stokes son útiles para un gran número de problemas prácticos, dentro das súas limitacións.
Notas[editar | editar a fonte]
- ↑ "Navier–Stokes Equation Clay Mathematics Institute". www.claymath.org. Arquivado dende o orixinal o 22 de decembro de 2015. Consultado o 2019-01-01.
Véxase tamén[editar | editar a fonte]
Bibliografía[editar | editar a fonte]
- White: MECÁNICA DE FLUÍDOS 5ª edición 2004 McGraw-Hill ISBN 84-481-4076-1. ISBN 978-84-481-4076-2
- Inge L. Rhyming Dynamique des fluides, 1991 PPUR
- A.D. Polyanin, A.M. Kutepov, A.V. Vyazmin, e D.A. Kazenin, Hydrodynamics, Mass and Heat Transfer in Chemical Engineering, Taylor & Francis, Londres, 2002. ISBN 0-415-27237-8
















































![{\displaystyle \rho {\frac {Du_{i}}{Dt}}=f_{i}-{\frac {\partial p}{\partial x_{i}}}+{\frac {\partial }{\partial x_{j}}}\left[2\mu \left(e_{ij}-{\frac {\Delta \delta _{ij}}{3}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee5cf61374bb6f0e6f36831b925bc2c34bce73cf)








![{\displaystyle \rho \left({\partial v_{x} \over \partial t}+v_{x}{\partial v_{x} \over \partial x}+v_{y}{\partial v_{x} \over \partial y}+v_{z}{\partial v_{x} \over \partial z}\right)=\mu \left[{\partial ^{2}v_{x} \over \partial x^{2}}+{\partial ^{2}v_{x} \over \partial y^{2}}+{\partial ^{2}v_{x} \over \partial z^{2}}\right]-{\partial p \over \partial x}+\rho g_{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa8820475e9c7b7606cb38f0a2157cbc021e8f0e)
![{\displaystyle \rho \left({\partial v_{y} \over \partial t}+v_{x}{\partial v_{y} \over \partial x}+v_{y}{\partial v_{y} \over \partial y}+v_{z}{\partial v_{y} \over \partial z}\right)=\mu \left[{\partial ^{2}v_{y} \over \partial x^{2}}+{\partial ^{2}v_{y} \over \partial y^{2}}+{\partial ^{2}v_{y} \over \partial z^{2}}\right]-{\partial p \over \partial y}+\rho g_{y}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e7cd99c16d16fdea688f0d68655d18a03e326d46)
![{\displaystyle \rho \left({\partial v_{z} \over \partial t}+v_{x}{\partial v_{z} \over \partial x}+v_{y}{\partial v_{z} \over \partial y}+v_{z}{\partial v_{z} \over \partial z}\right)=\mu \left[{\partial ^{2}v_{z} \over \partial x^{2}}+{\partial ^{2}v_{z} \over \partial y^{2}}+{\partial ^{2}v_{z} \over \partial z^{2}}\right]-{\partial p \over \partial z}+\rho g_{z}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/82ef96cc80ee7ad196ade223ba3e6a7a19176999)