Centroide (Baricentro)

Baricentro (Centroide) dun triángulo

En matemáticas e física, o baricentro ou centroide, tamén coñecido como centro xeométrico, dunha figura plana ou sólida é a posición media aritmética de todos os puntos da superficie da figura. A mesma definición esténdese a calquera obxecto nun espazo euclidiano n-dimensional.

En xeometría, adóitase asumir unha densidade de masa uniforme, nese caso o baricentro ou centro de masas coincide co centroide. Informalmente, pódese entender como o punto no que un obxecto (con masa uniformemente distribuída) podería estar perfectamente equilibrado na punta dun alfinete.

En xeografía, o centroide dunha proxección radial dunha rexión da superficie terrestre ata o nivel do mar é o centro xeográfico da rexión.

Propiedades

O centroide xeométrico dun obxecto convexo sempre reside no obxecto. Un obxecto non convexo pode ter un centroide que estea fóra da propia figura. O centroide dun anel ou dunha cunca, por exemplo, atópase no oco central do obxecto.

Se o centroide está definido, é un punto fixo de todas as isometrías do seu grupo de simetría. En particular, o centroide xeométrico dun obxecto atópase na intersección de todos os seus hiperplanos de simetría. O centroide de moitas figuras (polígono regular, poliedro regular, cilindro, rectángulo, rombo, círculo, esfera, elipse, elipsoide, superelipse, superelipsoide, etc.) pódese determinar só por este principio.

En particular, o centroide dun paralelogramo é o punto de encontro das súas dúas diagonais. Isto non é certo para outros cuadriláteros.

Polo mesmo motivo, o centroide dun obxecto con simetría de translación non está definido (ou está fóra do espazo circundante), porque unha translación non ten punto fixo.

Exemplos

O baricentro dun triángulo é a intersección das tres medianas do triángulo (cada mediana conecta un vértice co punto medio do lado oposto).

Determinación

Dun conxunto finito de puntos

O centroide dun conxunto finito de $k$ puntos $\mathbf {x} _{1},\mathbf {x} _{2},\ldots ,\mathbf {x} _{k}$ en $\mathbb {R} ^{n}$ é $$\mathbf {C} ={\frac {\mathbf {x} _{1}+\mathbf {x} _{2}+\cdots +\mathbf {x} _{k}}{k}}.$$Este punto minimiza a suma das distancias euclidianas ao cadrado entre el mesmo e cada punto do conxunto.

Por descomposición xeométrica

O centroide dunha figura plana $X$ pódese calcular dividíndoo nun número finito de figuriñas máis sinxelas $X_{1},X_{2},\dots ,X_{n},$ calculando o centroide $C_{i}$ e zona $A_{i}$ de cada parte, e despois calculando para as coordenadas x e y

$$C_{x}={\frac {\sum _{i}{C_{i}}_{x}A_{i}}{\sum _{i}A_{i}}},\quad C_{y}={\frac {\sum _{i}{C_{i}}_{y}A_{i}}{\sum _{i}A_{i}}}.$$

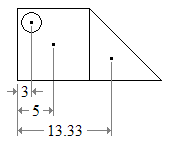
Por exemplo, a figura seguinte (a) divídese facilmente nun cadrado e nun triángulo, ambos con área positiva; e un buraquiño circular, con área negativa (b).

(a) 2D Obxecto

(b) Obxecto descrito utilizando elementos máis sinxelos

(c) Centroides dos elementos do obxecto

O centroide de cada parte pódese atopar nunha lista de centroides de formas simples (c). Logo, o centroide da figura é a media ponderada dos tres puntos. A posición horizontal do centroide, dende o bordo esquerdo da figura é $$x={\frac {5\times 10^{2}+13.33\times {\frac {1}{2}}10^{2}-3\times \pi 2.5^{2}}{10^{2}+{\frac {1}{2}}10^{2}-\pi 2.5^{2}}}\approx 8.5{\text{ unidades}}.$$ A posición vertical do centroide atópase do mesmo xeito.

A mesma fórmula vale para calquera subconxunto de $\mathbb {R} ^{d},$ para calquera dimensión $d,$ coas áreas substituídas polas $d$-medidas dimensionais das pezas.

Por fórmula integral

O centroide dun subconxunto $X$ de $\mathbb {R} ^{n}$ tamén se pode calcular mediante a fórmula

$$C={\frac {\int xg(x)\ dx}{\int g(x)\ dx}}$$

onde as integrais son tomadas sobre todo o espazo $\mathbb {R} ^{n},$ e $g$ é a función indicadora do subconxunto $X$ de $\mathbb {R} ^{n}\!:\ g(x)=1$ se $x\in X$ e $g(x)=0$ en caso contrario. Teña en conta que o denominador é simplemente a medida do conxunto $X.$ Esta fórmula non se pode aplicar se o conxunto $X$ ten medida cero, ou se calquera das integrais diverxe.

Dunha rexión delimitada

O centroide $({\bar {x}},\;{\bar {y}})$ dunha rexión limitada polas gráficas das funcións continuas $f$ e $g$ tal que $f(x)\geq g(x)$ no intervalo $[a,b],$$a\leq x\leq b$ está dada por

$${\begin{aligned}{\bar {x}}&={\frac {1}{A}}\int _{a}^{b}x{\bigl (}f(x)-g(x){\bigr )}\,dx,\\[5mu]{\bar {y}}&={\frac {1}{A}}\int _{a}^{b}{\tfrac {1}{2}}{\bigl (}f(x)+g(x){\bigr )}{\bigl (}f(x)-g(x){\bigr )}\,dx,\end{aligned}}$$

onde $A$ é a área da rexión (dada por ${\textstyle \int _{a}^{b}{\bigl (}f(x)-g(x){\bigr )}dx}$ ).

Dun triángulo

Artigo principal: Centros do triángulo.

O centroide ou baricentro dun triángulo é o punto de intersección das súas medianas (as liñas que unen cada vértice co punto medio do lado oposto). O centroide divide cada unha das medianas na relación $2:1,$ é dicir está situado ${\tfrac {1}{3}}$ da distancia de cada lado ao vértice oposto (ver as figuras laterais). As súas coordenadas cartesianas son as medias das coordenadas dos tres vértices. É dicir, se os tres vértices o son $L=(x_{L},y_{L}),$$M=(x_{M},y_{M}),$ e $N=(x_{N},y_{N}),$ a continuación, o centroide (indicado $C$ aquí pero denotado máis habitualmente $G$ en xeometría do triángulo ) é

$$C={\tfrac {1}{3}}(L+M+N)={\bigl (}{\tfrac {1}{3}}(x_{L}+x_{M}+x_{N}),{\tfrac {1}{3}}(y_{L}+y_{M}+y_{N}){\bigr )}.$$

O centroide está polo tanto en ${\tfrac {1}{3}}:{\tfrac {1}{3}}:{\tfrac {1}{3}}$ en coordenadas baricéntricas.

En coordenadas triliniares o centroide pódese expresar de calquera destes xeitos equivalentes en termos de lonxitudes dos lados $a,b,c$ e ángulos vértices $L,M,N$:

$${\begin{aligned}C&={\frac {1}{a}}:{\frac {1}{b}}:{\frac {1}{c}}=bc:ca:ab=\csc L:\csc M:\csc N\\[6pt]&=\cos L+\cos M\cdot \cos N:\cos M+\cos N\cdot \cos L:\cos N+\cos L\cdot \cos M\\[6pt]&=\sec L+\sec M\cdot \sec N:\sec M+\sec N\cdot \sec L:\sec N+\sec L\cdot \sec M.\end{aligned}}$$

O centroide tamén é o centro físico de masas se o triángulo está feito dunha folla uniforme de material.

O conxugado isogonal do centroide dun triángulo é o seu punto simediano.

Dun polígono

O centroide dun polígono pechado non autointersecante definido por $n$ vértices $(x_{0},y_{0}),\;$$(x_{1},y_{1}),\;\ldots ,\;$$(x_{n-1},y_{n-1}),$ é o punto $(C_{x},C_{y}),$

$$C_{\mathrm {x} }={\frac {1}{6A}}\sum _{i=0}^{n-1}(x_{i}+x_{i+1})(x_{i}\ y_{i+1}-x_{i+1}\ y_{i}),$$

$$C_{\mathrm {y} }={\frac {1}{6A}}\sum _{i=0}^{n-1}(y_{i}+y_{i+1})(x_{i}\ y_{i+1}-x_{i+1}\ y_{i}),$$

e onde $A$ é a área con signo do polígono, como se describe pola fórmula da área de Gauss:

$$A={\frac {1}{2}}\sum _{i=0}^{n-1}(x_{i}\ y_{i+1}-x_{i+1}\ y_{i}).$$

Nestas fórmulas, suponse que os vértices están numerados por orde de aparición ao longo do perímetro do polígono; ademais, o vértice $(x_{n},y_{n})$ suponse que é o mesmo que $(x_{0},y_{0}),$ pechando o polígono.

Dun tetraedro e un simplex n-dimensional

Un tetraedro é un obxecto no espazo tridimensional que ten como caras catro triángulos. Un segmento de liña que une un vértice dun tetraedro co centroide da cara oposta chámase mediana, e un segmento de liña que une os puntos medios de dúas arestas opostas chámase bimediana. Polo tanto, hai catro medianas e tres bimedianas. Estes sete segmentos de liña reúnense no centroide do tetraedro. As medianas divídense polo centroide na relación $3:1.$ O centroide dun tetraedro é o punto medio entre o seu punto de Monge e o circuncentro (centro da esfera circunscrita). Estes tres puntos definen a recta de Euler do tetraedro que é análoga á recta de Euler dun triángulo.

Estes resultados xeneralízanse a calquera simplex $n$-dimensional do seguinte xeito. Se o conxunto de vértices dun simplex é ${v_{0},\ldots ,v_{n}},$ entón considerando os vértices como vectores, o centroide é

$$C={\frac {1}{n+1}}\sum _{i=0}^{n}v_{i}.$$

O centroide xeométrico coincide co centro de masas se a masa se distribúe uniformemente por todo o simplex ou se concentra nos vértices como $n+1$ masas iguais.

Véxase tamén

Bibliografía

• Altshiller-Court, Nathan (1925). College Geometry: An Introduction to the Modern Geometry of the Triangle and the Circle (2nd ed.). New York: Barnes & Noble. LCCN 52013504. 
• Bourke, Paul (xullo 1997). "Calculating the area and centroid of a polygon". 
• Johnson, Roger A. (2007). Advanced Euclidean Geometry. Dover. 
• Kay, David C. (1969). College Geometry. New York: Holt, Rinehart and Winston. LCCN 69012075. 
• Larson, Roland E.; Hostetler, Robert P.; Edwards, Bruce H. (1998). Calculus of a Single Variable (6th ed.). Houghton Mifflin Company. 
• Protter, Murray H.; Morrey, Charles B. Jr. (1970). College Calculus with Analytic Geometry (2nd ed.). Reading: Addison-Wesley. LCCN 76087042. 
• Sangwin, C.J. Locating the centre of mass by mechanical means (PDF). Arquivado dende o orixinal (PDF) o 13 de novembro de 2013. 

Outros artigos

• Centro de Chebyshev
• algoritmo das k-medias
• Lista de centroides
• Teorema de Pappus-Guldin

Ligazóns externas

• Weisstein, Eric W. "Geometric Centroid". MathWorld. 
• Encyclopedia of Triangle Centers by Clark Kimberling. O baricentro está indicado como X(2).
• Characteristic Property of Centroid en cut-the-knot
• Animacións interactivas a mostrar o baricentro do triángulo e a construción do centroide con compás e regra
• procura experimentalmente as medianas e o centroide dun triángulo en Dynamic Geometry Sketches, un bosquexo interactivo de xeometría dinámica usando o simulador de gravidade de Cinderella.