Hipótese de Riemann

En matemática pura, a hipótese de Riemann, formulada por primeira vez por Bernhard Riemann en 1859, é unha conxectura sobre a distribución dos ceros da función zeta de Riemann ζ(s).[1]
A hipótese de Riemann, pola súa relación coa distribución dos números primos no conxunto dos naturais, é un dos problemas abertos máis importantes na matemática contemporánea.
O Instituto Clay de Matemáticas ofreceu un premio dun millón de dólares á primeira persoa que desenvolva unha demostración correcta da conxectura.[2] A maior parte da comunidade matemática pensa que a conxectura é correcta, aínda que outros grandes matemáticos como J. E. Littlewood e Atle Selberg se mostraron escépticos, aínda que o escepticismo de Selberg foi diminuíndo dende os seus días de mocidade. Nun artigo en 1989 suxeriu que un análogo debe ser certo para unha clase moito máis ampla de funcións (a clase de Selberg).
Definición
[editar | editar a fonte]A función zeta de Riemann ζ(s) está definida da seguinte maneira:
Para todos os números complexos s ≠ 1, pódese prolongar analiticamente mediante a ecuación funcional:
Esta posúe certos valores, chamados ceros "triviais" para os cales a función zeta se anula. Da ecuación pódese ver que s = −2, s = −4, s = −6, ... son ceros triviais. Existen outros valores complexos s comprendidos entre 0 < Re(s) < 1, para os cales a función zeta tamén se anula, chamados ceros "non triviais". A conxectura de Riemann fai referencia a estes ceros non triviais afirmando:
A parte real de todo cero non trivial da función zeta de Riemann é 1/2
Por tanto os ceros non triviais deberían atoparse na liña crítica s = 1/2 + it onde t é un número real e i é a unidade imaxinaria. A función zeta de Riemann, ao longo da liña crítica foi estudada en termos da función Z, cuxos ceros corresponden aos ceros da función zeta sobre a liña crítica.
Todos os ceros non triviais da función zeta de Riemann teñen unha parte real igual a 1/2?
Historia
[editar | editar a fonte]Riemann mencionou a conxectura en 1859, que sería chamada a hipótese de Riemann, na súa tese de doutoramento Sobre os números primos menores que unha magnitude dada, ao desenvolver unha fórmula explícita para calcular a cantidade de primos menores que x. Posto que non era esencial para o propósito central do seu artigo, non tentou dar unha demostración da mesma. Riemann sabía que os ceros non triviais da función zeta están distribuídos ao redor da recta s = 1/2 + it, e sabía tamén que todos os ceros non triviais debían estar no rango 0 ≤ Re(s) ≤ 1.[3]
En 1896, Hadamard e de la Vallée-Poussin probaron independentemente, que ningún cero podía estar sobre a recta Re(s) = 1. Xunto coas outras propiedades dos ceros non triviais demostradas por Riemann, isto mostrou que todos os ceros non triviais deben estar no interior da banda crítica 0 < Re(s) < 1. Este foi un paso fundamental para as primeiras demostracións do teorema dos números primos.
En 1900, Hilbert incluíu a hipótese de Riemann na súa famosa lista dos 23 problemas non resoltos: é parte do problema 8 na lista de Hilbert xunto coa conxectura de Goldbach. Cando se lle preguntou que faría se se espertase tras durmir cincocentos anos, Hilbert contestou que a súa primeira pregunta sería se a hipótese de Riemann fora probada. A hipótese de Riemann é o único problema dos que propuxo Hilbert que está no premio do milenio do Instituto Clay de Matemáticas.
En 1914, Hardy demostrou que existe un número infinito de ceros sobre a recta crítica Re(s) = 1/2. Con todo aínda era posible que un número infinito (e posiblemente a maioría) dos ceros non triviais se atopasen nalgún outro lugar sobre a banda crítica. En traballos posteriores de Hardy e Littlewood en 1921 e de Selberg en 1942 déronse estimacións para a densidade media dos ceros sobre a liña crítica.
Traballos recentes concentráronse no cálculo explícito da localización de grandes cantidades de ceros (coa esperanza de achar algún contraexemplo) e no establecemento de límites superiores na proporción de ceros que poidan estar lonxe da liña crítica (coa esperanza de reducilas a cero).
A hipótese de Riemann e os números primos
[editar | editar a fonte]A formulación tradicional da hipótese de Riemann escurece un pouco a importancia real da conxectura. A función zeta de Riemann ten unha profunda conexión cos números primos e Helge von Koch demostrou en 1901 que a hipótese de Riemann é equivalente ao considerable refinamento do teorema dos números primos: Existe unha constante C > 0 tal que
para todo x suficientemente grande, onde π(x) é a función contadora de primos e ln(x) é o logaritmo neperiano de x. Lowell Schoenfeld mostrou que se pode tomar C = 1/(8 π) para todo x ≥ 2657.
Os ceros da función zeta e os números primos satisfán certas propiedades de dualidade, coñecidas como fórmulas explícitas, que mostran, usando análises de Fourier, que os ceros da función zeta de Riemann poden interpretarse como frecuencias harmónicas na distribución dos números primos.
Máis aínda, se a conxectura de Hilbert-Polya é certa, entón calquera operador que nos dea as partes imaxinarias dos ceros como os seus valores propios debe satisfacer:
onde tr é a traza do operador (suma dos seus valores propios), é un número imaxinario e é a función de Chebyshev que suma o log(x) sobre os primos e as súas potencias enteiras, dita fórmula é unha conclusión da fórmula explícita de V. Mangoldt.[4] Varios operadores propostos por C. Perelman, J. Macheca e J. García, parecen corroborar os resultados da conxectura de Hilbert sobre o operador, reproducindo a parte imaxinaria dos ceros.
Cálculo numérico
[editar | editar a fonte]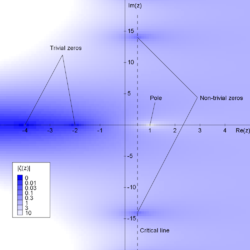
No ano 2004 Xavier Gourdon verificou a conxectura de Riemann numericamente ao longo do primeiros dez trillóns de ceros non triviais da función. Con todo, isto non é estritamente unha demostración e numericamente sería máis interesante atopar un contraexemplo, é dicir un valor de cero que non cumpra con que a súa parte real é 1/2, pois isto botaría polos chans a validez da conxectura.
Até o 2005, o intento máis serio para explorar os ceros da función-ζ, é o ZetaGrid, un proxecto de computación distribuída coa capacidade de verificar billóns de ceros por día. O proxecto acabou en decembro de 2005, e ningún dos ceros puido ser identificado como contraexemplo da hipótese de Riemann.
Notas
[editar | editar a fonte]- ↑ Bombieri, Enrico (2000). The Riemann Hypothesis - official problem description (PDF) (en inglés). Clay Mathematics Institute. Consultado o 21-2-2011.. Reimpreso en (Borwein et al. 2008).
- ↑ «The Millennium Prize Problems» Arquivado 08 de xaneiro de 2008 en Wayback Machine. (en inglés).
- ↑ Riemann, Bertrand (1859). "Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse". Consultado o 29-12-2008.
- ↑ "Fórmula explícita" (PDF). Arquivado dende o orixinal (PDF) o 19 de xuño de 2010. Consultado o 15 de xaneiro de 2017.
Véxase tamén
[editar | editar a fonte]Outros artigos
[editar | editar a fonte]Ligazóns externas
[editar | editar a fonte]- The Riemann Hypothesis in a Nutshell Arquivado 15 de xuño de 2008 en Wayback Machine. (en inglés)
- Andrew Odlyzko: Tables of zeros of the Riemann zeta function (en inglés)
- Riemann zeros Quantum chaos (en inglés)
- Zetagrid (en inglés)
- Algoritmos para calcular os ceros da función de Riemann, por Michael Rubinstein (en inglés)




![{\displaystyle \sum _{n}e^{-\beta E_{n}}=\operatorname {tr} [e^{-\beta {\hat {H}}}]=e^{u/2}-e^{-u/2}{\frac {d\psi _{0}}{du}}-{\frac {e^{u/2}}{e^{3u}-e^{u}}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/89764162348181454cda8b451b58cf0066636006)

