Función zeta de Riemann

A función zeta de Riemann ζ(s) trazada con cor de dominio.

O polo en $s=1$ e dous ceros na liña crítica.

A función zeta de Riemann, denotada pola letra grega ζ (zeta ), é unha función matemática dunha variábel complexa definida como $$\zeta (s)=\sum _{n=1}^{\infty }{\frac {1}{n^{s}}}={\frac {1}{1^{s}}}+{\frac {1}{2^{s}}}+{\frac {1}{3^{s}}}+\cdots$$ para $\operatorname {Re} (s)>1$, e a súa continuación analítica para unha variábel complexa.

A función zeta de Riemann xoga un papel fundamental na teoría analítica de números, e ten aplicacións en física, teoría da probabilidade e estatística aplicada.

Leonhard Euler introduciu e estudou por primeira vez a función sobre os reais na primeira metade do século XVIII. O artigo de Bernhard Riemann de 1859 "Sobre o número de primos menores que unha magnitude dada" estendeu a definición de Euler a unha variable complexa, demostrou a súa continuación meromorfa e a súa ecuación funcional e estabeleceu unha relación entre os seus ceros e a distribución dos números primos. Ese artigo tamén contiña a hipótese de Riemann, unha conxectura sobre a distribución dos ceros complexos da función zeta de Riemann que moitos matemáticos consideran o problema sen resolver máis importante da matemática pura.

Euler calculou os valores da función zeta de Riemann para enteiros positivos pares. O primeiro deles, ζ(2), proporciona unha solución ao problema de Basilea. En 1979 Roger Apéry demostrou a irracionalidade de ζ(3). Os valores en puntos enteiros negativos, tamén atopados por Euler, son números racionais e xogan un papel importante na teoría das formas modulares. Coñécense varias xeneralizacións da función zeta de Riemann, como as series de Dirichlet, as L-funcións e as L-funcións de Dirichlet.

Definición

A función zeta de Riemann ζ(s) é unha función dunha variábel complexa s = σ + it, onde σ e t son números reais. (A notación s, σ e t utilízase tradicionalmente no estudo da función zeta, seguindo a Riemann.) Cando Re(s) = σ > 1, a función pódese escribir como unha suma converxente ou como unha integral:

$\zeta (s)=\sum _{n=1}^{\infty }{\frac {1}{n^{s}}}={\frac {1}{\Gamma (s)}}\int _{0}^{\infty }{\frac {x^{s-1}}{e^{x}-1}}\,\mathrm {d} x\,$

onde

$\Gamma (s)=\int _{0}^{\infty }x^{s-1}\,e^{-x}\,\mathrm {d} x$

é a función gamma. A función zeta de Riemann defínese para outros valores complexos mediante a continuación analítica da función definida para σ > 1.

A serie anterior é unha serie de Dirichlet prototípica que converxe absolutamente nunha función analítica para s tal que σ > 1 e diverxe para todos os demais valores de s. Riemann demostrou que a función definida pola serie no semiplano de converxencia pode continuarse analíticamente ata todos os valores complexos s ≠ 1. Para s = 1, a serie correspóndese coa serie harmónica que diverxe cara a +∞ e

$\lim _{s\to 1}(s-1)\zeta (s)=1.$

Así, a función zeta de Riemann é unha función meromorfa en todo o plano complexo, que é holomorfa en todas as partes agás nun polo simple en s = 1 con residuo 1.

Fórmula do produto de Euler

En 1737, a conexión entre a función zeta e os números primos foi descuberta por Euler, quen probou a identidade

$\zeta (s)=\sum _{n=1}^{\infty }{\frac {1}{n^{s}}}=\prod _{p{\text{ primo}}}{\frac {1}{1-p^{-s}}},$

onde o produto infinito do lado dereito esténdese sobre todos os números primos p (esas expresións chámanse produtos de Euler):

$\prod _{p{\text{ primo}}}{\frac {1}{1-p^{-s}}}={\frac {1}{1-2^{-s}}}\cdot {\frac {1}{1-3^{-s}}}\cdot {\frac {1}{1-5^{-s}}}\cdot {\frac {1}{1-7^{-s}}}\cdot {\frac {1}{1-11^{-s}}}\cdots {\frac {1}{1-p^{-s}}}\cdots$

A fórmula do produto de Euler pódese usar para calcular a probabilidade asintótica de que s enteiros seleccionados aleatoriamente sexan coprimos.

Esta probabilidade asintótica de que s enteiros sexan coprimos está dada por

$\prod _{p{\text{ primo}}}\left(1-{\frac {1}{p^{s}}}\right)=\left(\prod _{p{\text{ primo}}}{\frac {1}{1-p^{-s}}}\right)^{-1}={\frac {1}{\zeta (s)}}.$

Ecuación funcional de Riemann

Esta función zeta satisfai a ecuación funcional $$\zeta (s)=2^{s}\pi ^{s-1}\ \sin \left({\frac {\pi s}{2}}\right)\ \Gamma (1-s)\ \zeta (1-s),$$onde Γ(s) é a función gamma. Esta é unha igualdade de funcións meromorfas válida en todo o plano complexo. A ecuación relaciona os valores da función zeta de Riemann nos puntos s e 1 − s, en particular relacionando enteiros pares positivos con enteiros negativos impares. Debido aos ceros da función seno, a ecuación funcional implica que ζ(s) ten un cero simple en cada número enteiro par negativo s = −2n, coñecidos como ceros triviais de ζ(s).

Cando s é un enteiro positivo par, o produto sin(πs/2)Γ(1 − s) no lado dereito é distinto de cero porque Γ(1 − s) ten un polo, que cancela o cero simple do factor seno.

Os ceros, a liña crítica e a hipótese de Riemann

Artigo principal: hipótese de Riemann.

Espiral zeta de Riemann ao longo da liña crítica desde a altura 999000 ata un millón (de vermello a violeta)

A función zeta de Riemann non ten ceros á dereita de σ = 1 ou (ademais dos ceros triviais) á esquerda de σ = 0 (tampouco os ceros poden estar demasiado preto desas liñas). A maiores, os ceros non triviais son simétricos sobre o eixo real e a recta σ = 1/2

Esta imaxe mostra unha gráfica da función zeta de Riemann ao longo da liña crítica para os valores reais de t que van de 0 a 34. Os primeiros cinco ceros da franxa crítica son claramente visíbeis como o lugar onde pasan as espirais pola orixe.

A parte real (vermello) e a parte imaxinaria (azul) da función zeta de Riemann ao longo da recta crítica Re( s ) = 1/2. Os primeiros ceros non triviais pódense ver en Im( s ) = ±14,135, ±21,022 e ±25,011.

Animación que mostra a función zeta de Riemann ao longo da liña crítica. Zeta(1/2 + I y) para y que varía de 1000 a 1005.

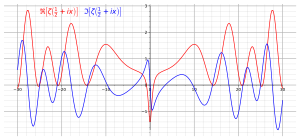
A ecuación funcional mostra que a función zeta de Riemann ten ceros en −2, −4, -6, .... Estes chámanse ceros triviais. Son triviais no sentido de que a súa existencia é fáciliña de demostrar, por exemplo, porque sin πs/2 é 0 na ecuación funcional. Os ceros non triviais captaron moita máis atención porque a súa distribución non só se entende moito menos senón que, o que é máis importante, o seu estudo provoca resultados importantes en relación cos números primos e outros elementos relacionados na teoría de números. Sábese que calquera cero non trivial está na franxa aberta $\{s\in \mathbb {C} :0<\operatorname {Re} (s)<1\}$, que se chama a franxa crítica. O conxunto $\{s\in \mathbb {C} :\operatorname {Re} (s)=1/2\}$ chámase liña crítica. A hipótese de Riemann, considerada un dos maiores problemas sen resolver en matemáticas, afirma que todos os ceros non triviais están na liña crítica. En 1989, Conrey demostrou que máis do 40% dos ceros non triviais da función zeta de Riemann están na liña crítica.

Para a función zeta de Riemann na liña crítica, consulte Z-función.

Primeiros ceros non triviais

Cero
1/2 ± 14,134725 i
1/2 ± 21,022040 i
1/2 ± 25,010858 i
1/2 ± 30,424876 i
1/2 ± 32,935062 i
1/2 ± 37,586178 i
1/2 ± 40,918719 i

Número de ceros na franxa crítica

Sexa $N(T)$ o número de ceros de $\zeta (s)$ na franxa crítica $0<\operatorname {Re} (s)<1$, cuxas partes imaxinarias están no intervalo $0<\operatorname {Im} (s)<T$. Trudgian demostrou que, se $T>e$, entón

$\left|N(T)-{\frac {T}{2\pi }}\log {\frac {T}{2\pi e}}\right|\leq 0.112\log T+0.278\log \log T+3.385+{\frac {0.2}{T}}$.

As conxecturas de Hardy-Littlewood

En 1914, G. H. Hardy demostrou que ζ (1/2 + it) ten infinitos ceros reais.

Hardy e J. E. Littlewood formulou dúas conxecturas sobre a densidade e a distancia entre os ceros de ζ (1/2 + it) en intervalos de grandes números reais positivos. A continuación, N(T) é o número total de ceros reais e N₀( T) o número total de ceros de orde impar da función ζ (1/2 + it) situada no intervalo (0, T].

• Para calquera ε > 0, existe un T₀(ε) > 0 tal que cando

$T\geq T_{0}(\varepsilon )\quad {\text{ e }}\quad H=T^{{\frac {1}{4}}+\varepsilon },$

o intervalo (T, T + H] contén un cero de orde impar.

• Para calquera ε > 0, existe un T₀(ε) > 0 e c_ε > 0 tal que a desigualdade

$N_{0}(T+H)-N_{0}(T)\geq c_{\varepsilon }H$ cúmprese cando $T\geq T_{0}(\varepsilon ){\text{ e }}H=T^{{\frac {1}{2}}+\varepsilon }.$

Estas dúas conxecturas abriron novas direccións na investigación da función zeta de Riemann.

Rexión sen ceros

A localización dos ceros da función zeta de Riemann é de gran importancia na teoría de números. O teorema dos números primos é equivalente ao feito de que non hai ceros da función zeta na liña Re(s) = 1. Un mellor resultado , que se desprende dunha forma efectiva do teorema do valor medio de Vinogradov, é que ζ (σ + it) ≠ 0 sempre que $\sigma \geq 1-{\frac {1}{57.54(\log {|t|})^{\frac {2}{3}}(\log {\log {|t|}})^{\frac {1}{3}}}}$ e |t| ≥ 3.

En 2015, Mossinghoff e Trudgian demostraron que zeta non ten ceros na rexión

$\sigma \geq 1-{\frac {1}{5.573412\log |t|}}$ para |t| ≥ 2.

Esta é a maior rexión libre de ceros coñecida na franxa crítica para $3.06\cdot 10^{10}<|t|<\exp(10151.5)\approx 5.5\cdot 10^{4408}$.

O resultado máis forte deste tipo que se pode esperar é a verdade da hipótese de Riemann, que tería moitas consecuencias profundas na teoría dos números.

Valores específicos

Artigo principal: Valores específicos da función zeta de Riemann.

Para calquera enteiro par positivo 2n,

$\zeta (2n)={\frac {|{B_{2n}}|(2\pi )^{2n}}{2(2n)!}},$

onde B_2n é o 2n-ésimo número de Bernoulli.

Para os números enteiros positivos impares, non se coñece ningunha expresión simple, consulte Valores especiais das L-funcións.

O cálculo de $\zeta (2)$ coñécese como o problema de Basilea. O valor de $\zeta (4)$ está relacionado coa Lei de Stefan–Boltzmann e a aproximación de Viena en física. Os primeiros valores son:

${\begin{aligned}\zeta (2)&=1+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+\cdots ={\frac {\pi ^{2}}{6}}\\[4pt]\zeta (4)&=1+{\frac {1}{2^{4}}}+{\frac {1}{3^{4}}}+\cdots ={\frac {\pi ^{4}}{90}}\\[4pt]\zeta (6)&=1+{\frac {1}{2^{6}}}+{\frac {1}{3^{6}}}+\cdots ={\frac {\pi ^{6}}{945}}\\[4pt]\zeta (8)&=1+{\frac {1}{2^{8}}}+{\frac {1}{3^{8}}}+\cdots ={\frac {\pi ^{8}}{9450}}\\[4pt]\zeta (10)&=1+{\frac {1}{2^{10}}}+{\frac {1}{3^{10}}}+\cdots ={\frac {\pi ^{10}}{93555}}\\[4pt]\zeta (12)&=1+{\frac {1}{2^{12}}}+{\frac {1}{3^{12}}}+\cdots ={\frac {691\pi ^{12}}{638512875}}.\end{aligned}}$

Tomando o límte cando $n\rightarrow \infty$, obtemos $\zeta (\infty )=1$. Mais no infinito complexo da esfera de Riemann a función zeta ten unha singularidade esencial.

Valores seleccionados para enteiros pares

Valor	Expansión decimal	Secuencia OEIS
$\zeta (2)$	1.6449340668482264364...	(secuencia A013661 na OEIS)
$\zeta (4)$	1.0823232337111381915...	(secuencia A013662 na OEIS)
$\zeta (6)$	1.0173430619844491397...	(secuencia A013664 na OEIS)
$\zeta (8)$	1.0040773561979443393...	(secuencia A013666 na OEIS)
$\zeta (10)$	1.0009945751278180853...	(secuencia A013668 na OEIS)
$\zeta (12)$	1.0002460865533080482...	(secuencia A013670 na OEIS)

Para os enteiros non positivos, temos

$\zeta (-n)=-{\frac {B_{n+1}}{n+1}}$ para n ≥ 0 (usando a convención de que B₁ = 1/2).

A constante de Apéry é o valor

$\zeta (3)=1+{\frac {1}{2^{3}}}+{\frac {1}{3^{3}}}+\cdots =1.202056903159594285399...$.

Series diverxentes

A través da continuación analítica, pódese demostrar

$\zeta (-1)=-{\tfrac {1}{12}}$

Isto dá un pretexto para asignar un valor finito á serie diverxente 1 + 2 + 3 + 4 + ⋯, que se utilizou en certos contextos (Sumatorio de Ramanujan) como na teoría de cordas. De xeito análogo, o valor particular

$\zeta (0)=-{\tfrac {1}{2}}$

pódese ver como a asignación dun resultado finito á serie diverxente 1 + 1 + 1 + 1 + ⋯ .

O valor

$\zeta {\bigl (}{\tfrac {1}{2}}{\bigr )}=-1.46035450880958681288\ldots$

emprégase no cálculo de problemas de capa límite cinética de ecuacións cinéticas lineares. Aínda que

$\zeta (1)=1+{\tfrac {1}{2}}+{\tfrac {1}{3}}+\cdots$

diverxe, o seu principal valor de Cauchy

$\lim _{\varepsilon \to 0}{\frac {\zeta (1+\varepsilon )+\zeta (1-\varepsilon )}{2}}$

existe, sendo igual á constante de Euler-Mascheroni γ = 0.5772....

Representacións

Serie de Dirichlet

Pódese obter unha extensión da área de converxencia reordenando a serie orixinal. A serie

$\zeta (s)={\frac {1}{s-1}}\sum _{n=1}^{\infty }\left({\frac {n}{(n+1)^{s}}}-{\frac {n-s}{n^{s}}}\right)$

converxe para Re(s) > 0, mentres que

$\zeta (s)={\frac {1}{s-1}}\sum _{n=1}^{\infty }{\frac {n(n+1)}{2}}\left({\frac {2n+3+s}{(n+1)^{s+2}}}-{\frac {2n-1-s}{n^{s+2}}}\right)$

converxe mesmo para Re(s) > −1. Deste xeito, a área de converxencia pódese estender a Re(s) > −k para calquera número enteiro negativo −k.

A recorrencia é claramente visíbel coa expresión válida para Re(s) > −2 o que permite unha maior expansión mediante a integración por partes.

${\begin{aligned}\zeta (s)=&1+{\frac {1}{s-1}}-{\frac {s}{2!}}[\zeta (s+1)-1]\\-&{\frac {s(s+1)}{3!}}[\zeta (s+2)-1]\\&-{\frac {s(s+1)(s+2)}{3!}}\sum _{n=1}^{\infty }\int _{0}^{1}{\frac {t^{3}dt}{(n+t)^{s+3}}}.\end{aligned}}$

Integrais tipo Mellin

A transformada de Mellin dunha función f(x) defínese como

$\int _{0}^{\infty }f(x)x^{s}\,{\frac {\mathrm {d} x}{x}}$

na rexión onde a integral está definida. Hai varias expresións para a función zeta como integrais tipo transformada de Mellin. Se a parte real de s é maior que un, temos

$\Gamma (s)\zeta (s)=\int _{0}^{\infty }{\frac {x^{s-1}}{e^{x}-1}}\,\mathrm {d} x\quad$ e $\quad \Gamma (s)\zeta (s)={\frac {1}{2s}}\int _{0}^{\infty }{\frac {x^{s}}{\cosh(x)-1}}\,\mathrm {d} x$ ,

onde Γ denota a función gamma. Ao modificar o contorno, Riemann mostrou que

$2\sin(\pi s)\Gamma (s)\zeta (s)=i\oint _{H}{\frac {(-x)^{s-1}}{e^{x}-1}}\,\mathrm {d} x,$

para todo s (onde H denota o contorno de Hankel).

Tamén podemos atopar expresións relacionadas con números primos e co teorema dos números primos. Se π(x) é a función de contaxe de primos, entón

$\ln \zeta (s)=s\int _{0}^{\infty }{\frac {\pi (x)}{x(x^{s}-1)}}\,\mathrm {d} x,$

para valores con Re(s) > 1.

Funcións theta

A función zeta de Riemann pódese dar mediante unha transformada de Mellin

$2\pi ^{-{\frac {s}{2}}}\Gamma \left({\frac {s}{2}}\right)\zeta (s)=\int _{0}^{\infty }{\bigl (}\theta (it)-1{\bigr )}t^{{\frac {s}{2}}-1}\,\mathrm {d} t,$

en termos da función theta de Jacobi

$\theta (\tau )=\sum _{n=-\infty }^{\infty }e^{\pi in^{2}\tau }.$

No entanto, esta integral só converxe se a parte real de s é maior que 1, mais pódese regularizar. Isto dá a seguinte expresión para a función zeta, que está ben definida para todos os s agás 0 e 1:

$\pi ^{-{\frac {s}{2}}}\Gamma \left({\frac {s}{2}}\right)\zeta (s)={\frac {1}{s-1}}-{\frac {1}{s}}+{\frac {1}{2}}\int _{0}^{1}\left(\theta (it)-t^{-{\frac {1}{2}}}\right)t^{{\frac {s}{2}}-1}\,\mathrm {d} t+{\frac {1}{2}}\int _{1}^{\infty }{\bigl (}\theta (it)-1{\bigr )}t^{{\frac {s}{2}}-1}\,\mathrm {d} t.$

Serie de Laurent

A función zeta de Riemann é meromorfa cun só polo de orde un en s = 1. Polo tanto, pódese expandir como unha serie de Laurent en s = 1; o desenvolvemento da serie é logo

$\zeta (s)={\frac {1}{s-1}}+\sum _{n=0}^{\infty }{\frac {\gamma _{n}}{n!}}(1-s)^{n}.$

As constantes γ_n aquí chámanse constantes de Stieltjes e pódense definir polo límite

$\gamma _{n}=\lim _{m\rightarrow \infty }{\left(\left(\sum _{k=1}^{m}{\frac {(\ln k)^{n}}{k}}\right)-{\frac {(\ln m)^{n+1}}{n+1}}\right)}.$

O termo constante γ₀ é a constante de Euler-Mascheroni.

Factorial ascendente

Outro desenvolvemento en serie usando o factorial ascendente válido para todo o plano complexo é

$\zeta (s)={\frac {s}{s-1}}-\sum _{n=1}^{\infty }{\bigl (}\zeta (s+n)-1{\bigr )}{\frac {s(s+1)\cdots (s+n-1)}{(n+1)!}}.$

Transformada de Mellin do mapa de Engel

A función $g(x)=x\left(1+\left\lfloor x^{-1}\right\rfloor \right)-1$ itérase para atopar os coeficientes que aparecen nas expansións de Engel.

A transformada de Mellin do mapa $g(x)$ está relacionada coa función zeta de Riemann pola fórmula

${\begin{aligned}\int _{0}^{1}g(x)x^{s-1}\,dx&=\sum _{n=1}^{\infty }\int _{\frac {1}{n+1}}^{\frac {1}{n}}(x(n+1)-1)x^{s-1}\,dx\\[6pt]&=\sum _{n=1}^{\infty }{\frac {n^{-s}(s-1)+(n+1)^{-s-1}(n^{2}+2n+1)+n^{-s-1}s-n^{1-s}}{(s+1)s(n+1)}}\\[6pt]&={\frac {\zeta (s+1)}{s+1}}-{\frac {1}{s(s+1)}}.\end{aligned}}$

Algoritmos numéricos

Un algoritmo clásico, en uso antes de aproximadamente 1930, procede aplicando a fórmula de Euler-Maclaurin para obter, para n e m enteiros positivos,

$\zeta (s)=\sum _{j=1}^{n-1}j^{-s}+{\tfrac {1}{2}}n^{-s}+{\frac {n^{1-s}}{s-1}}+\sum _{k=1}^{m}T_{k,n}(s)+E_{m,n}(s)$

onde $B_{2k}$ denota o número de Bernoulli correspondente,

$T_{k,n}(s)={\frac {B_{2k}}{(2k)!}}n^{1-s-2k}\prod _{j=0}^{2k-2}(s+j)$

e o erro cumpre

$|E_{m,n}(s)|<\left|{\frac {s+2m+1}{\sigma +2m+1}}T_{m+1,n}(s)\right|,$con σ = Re(s).

Un algoritmo numérico moderno é o algoritmo de Odlyzko-Schönhage.

Xeneralizacións

Hai unha serie de funcións zeta relacionadas que poden considerarse xeneralizacións da función zeta de Riemann. Estas inclúen:

A función zeta de Hurwitz

$\zeta (s,q)=\sum _{k=0}^{\infty }{\frac {1}{(k+q)^{s}}}$.

O polilogaritmo

$\operatorname {Li} _{s}(z)=\sum _{k=1}^{\infty }{\frac {z^{k}}{k^{s}}}$.

O trascendente de Lerch

$\Phi (z,s,q)=\sum _{k=0}^{\infty }{\frac {z^{k}}{(k+q)^{s}}}$.

Véxase tamén

Bibliografía

• Recoméndase empregar os marcadores   e/ou  .

Outros artigos

• Ligazóns entre [[ ]].

Ligazóns externas

• Modelo:Commons category-inline
• "Zeta-function". Encyclopedia of Mathematics. EMS Press. 2001 [1994]. 
• Riemann Zeta Function, in Wolfram Mathworld — an explanation with a more mathematical approach
• Prime Numbers Get Hitched A general, non-technical description of the significance of the zeta function in relation to prime numbers.
• X-Ray of the Zeta Function Visually oriented investigation of where zeta is real or purely imaginary.
• Formulas and identities for the Riemann Zeta function functions.wolfram.com
• Riemann Zeta Function and Other Sums of Reciprocal Powers, section 23.2 of Abramowitz and Stegun
• Frenkel, Edward. "Million Dollar Math Problem". Brady Haran. Arquivado dende o orixinal (video) o 2021-12-11. Consultado o 11 marzo 2014. 
• Mellin transform and the functional equation of the Riemann Zeta function—Computational examples of Mellin transform methods involving the Riemann Zeta Function
• Visualizing the Riemann zeta function and analytic continuation a video from 3Blue1Brown