Función totiente de Euler

Os primeiros mil valores de φ(n). Os puntos da liña superior representan φ(p) cando p é un número primo, que é p − 1.

En teoría de números, a función totiente de Euler conta os enteiros positivos ata un número enteiro dado n que son coprimos con n. Escríbese usando a letra grega fi como $\varphi (n)$ ou $\phi (n)$, e tamén se pode chamar función fi de Euler. Noutras palabras, é o número de enteiros k no rango 1 ≤ k ≤ n para os que o máximo común divisor gcd(n, k) é igual a 1. Os números enteiros k desta forma denomínanse ás veces como totativos de n.

Por exemplo, os totativos de n = 9 son os seis números 1, 2, 4, 5, 7 e 8. Todos son relativamente primos para 9, mais os outros tres números deste rango, 3, 6 e 9 non o son, xa que gcd(9, 3) = gcd(9, 6) = 3 e gcd(9, 9) = 9 . Polo tanto, φ(9) = 6 . Como outro exemplo, φ(1) = 1 xa que para n = 1 o único enteiro no intervalo de 1 a n é o propio 1, e gcd(1, 1) = 1 .

A función totiente de Euler é unha función multiplicativa, o que significa que se dous números m e n son coprimos, daquela φ(mn) = φ(m)φ(n). Esta función dá a orde do grupo multiplicativo de enteiros módulo n (o grupo de unidades do anel $\mathbb {Z} /n\mathbb {Z}$). Tamén se usa para definir o sistema de cifrado RSA.

Historia, terminoloxía e notación

Leonhard Euler introduciu a función en 1763. Porén, non escolleu nese momento ningún símbolo específico para denotalo. Nunha publicación de 1784, Euler estudou máis a función, escollendo a letra grega π para denotala: escribiu πD para "a multitude de números inferiores a D, e que non teñen divisor común con ela". A notación agora estándar φ(A) provén do tratado Disquisitiones Arithmeticae de Gauss de 1801, aínda que Gauss non utilizou parénteses ao redor do argumento e escribiu φA. Así, a miúdo chámase función phi de Euler ou simplemente función phi.

En 1879, J.J. Sylvester acuñou o termo "totient" para esta función, polo que tamén se chama función totiente de Euler, totiente de Euler ou totiente de Euler.

O cototiente de n defínese como n − φ(n). Conta o número de enteiros positivos inferiores ou iguais a n que teñen polo menos un factor primo en común con n.

Cálculo da función total de Euler

Hai varias fórmulas para calcular φ(n) .

Fórmula do produto de Euler

$\varphi (n)=n\prod _{p\mid n}\left(1-{\frac {1}{p}}\right),$

onde o produto é sobre os distintos números primos que dividen n. (Para notación, consulte Función aritmética).

Unha formulación equivalente é $$\varphi (n)=p_{1}^{k_{1}-1}(p_{1}{-}1)\,p_{2}^{k_{2}-1}(p_{2}{-}1)\cdots p_{r}^{k_{r}-1}(p_{r}{-}1),$$ onde $n=p_{1}^{k_{1}}p_{2}^{k_{2}}\cdots p_{r}^{k_{r}}$ é a descomposición en factores primos de $n$ (é dicir, $p_{1},p_{2},\ldots ,p_{r}$ son números primos distintos).

A proba destas fórmulas depende de dous feitos importantes.

Phi é unha función multiplicativa

Isto significa que se gcd(m, n) = 1, daquela φ(m) φ(n) = φ(mn). Esquema de demostración: Sexan A, B, C os conxuntos de enteiros positivos que son coprimos e inferiores a m, n, mn, respectivamente, de xeito que |A| = φ(m), etc. Entón hai unha bixección entre A × B e C polo teorema chinés do resto.

Valor de phi para un argumento que sexa potencia dun primo

Se p é primo e k ≥ 1, daquela

$\varphi \left(p^{k}\right)=p^{k}-p^{k-1}=p^{k-1}(p-1)=p^{k}\left(1-{\tfrac {1}{p}}\right).$

Proba da fórmula do produto de Euler

O teorema fundamental da aritmética estabelece que se n > 1 hai unha expresión única $n=p_{1}^{k_{1}}p_{2}^{k_{2}}\cdots p_{r}^{k_{r}},$ onde p₁ < p₂ < ... < p_r son números primos e cada k_i ≥ 1. (O caso n = 1 corresponde ao produto baleiro) Usando repetidamente a propiedade multiplicativa de φ e a fórmula para φ(p^k) dá

${\begin{array}{rcl}\varphi (n)&=&\varphi (p_{1}^{k_{1}})\,\varphi (p_{2}^{k_{2}})\cdots \varphi (p_{r}^{k_{r}})\\[.1em]&=&p_{1}^{k_{1}}\left(1-{\frac {1}{p_{1}}}\right)p_{2}^{k_{2}}\left(1-{\frac {1}{p_{2}}}\right)\cdots p_{r}^{k_{r}}\left(1-{\frac {1}{p_{r}}}\right)\\[.1em]&=&p_{1}^{k_{1}}p_{2}^{k_{2}}\cdots p_{r}^{k_{r}}\left(1-{\frac {1}{p_{1}}}\right)\left(1-{\frac {1}{p_{2}}}\right)\cdots \left(1-{\frac {1}{p_{r}}}\right)\\[.1em]&=&n\left(1-{\frac {1}{p_{1}}}\right)\left(1-{\frac {1}{p_{2}}}\right)\cdots \left(1-{\frac {1}{p_{r}}}\right).\end{array}}$

Isto dá ambas as versións da fórmula do produto de Euler.

Exemplo

$\varphi (20)=\varphi (2^{2}5)=20\,(1-{\tfrac {1}{2}})\,(1-{\tfrac {1}{5}})=20\cdot {\tfrac {1}{2}}\cdot {\tfrac {4}{5}}=8.$

A fórmula alternativa usa só números enteiros: $$\varphi (20)=\varphi (2^{2}5^{1})=2^{2-1}(2{-}1)\,5^{1-1}(5{-}1)=2\cdot 1\cdot 1\cdot 4=8.$$

Transformada de Fourier

O totiente é a transformada discreta de Fourier do mcd, avaliada en 1. Sexa

${\mathcal {F}}\{\mathbf {x} \}[m]=\sum \limits _{k=1}^{n}x_{k}\cdot e^{{-2\pi i}{\frac {mk}{n}}}$

onde x_k = gcd(k,n) para k ∈ {1, ..., n}. Daquela

$\varphi (n)={\mathcal {F}}\{\mathbf {x} \}[1]=\sum \limits _{k=1}^{n}\gcd(k,n)e^{-2\pi i{\frac {k}{n}}}.$

A parte real desta fórmula é

$\varphi (n)=\sum \limits _{k=1}^{n}\gcd(k,n)\cos {\tfrac {2\pi k}{n}}.$

Por exemplo, usando $\cos {\tfrac {\pi }{5}}={\tfrac {{\sqrt {5}}+1}{4}}$ e $\cos {\tfrac {2\pi }{5}}={\tfrac {{\sqrt {5}}-1}{4}}$ : $${\begin{array}{rcl}\varphi (10)&=&\gcd(1,10)\cos {\tfrac {2\pi }{10}}+\gcd(2,10)\cos {\tfrac {4\pi }{10}}+\gcd(3,10)\cos {\tfrac {6\pi }{10}}+\cdots +\gcd(10,10)\cos {\tfrac {20\pi }{10}}\\&=&1\cdot ({\tfrac {{\sqrt {5}}+1}{4}})+2\cdot ({\tfrac {{\sqrt {5}}-1}{4}})+1\cdot (-{\tfrac {{\sqrt {5}}-1}{4}})+2\cdot (-{\tfrac {{\sqrt {5}}+1}{4}})+5\cdot (-1)\\&&+\ 2\cdot (-{\tfrac {{\sqrt {5}}+1}{4}})+1\cdot (-{\tfrac {{\sqrt {5}}-1}{4}})+2\cdot ({\tfrac {{\sqrt {5}}-1}{4}})+1\cdot ({\tfrac {{\sqrt {5}}+1}{4}})+10\cdot (1)\\&=&4.\end{array}}$$ A diferenza do produto de Euler e da fórmula da suma dos divisores, esta fórmula non require coñecer os factores de n. Porén, implica o cálculo do máximo común divisor de n e de cada número enteiro positivo menor que n, o que é abondo para proporcionar a factorización.

Suma de divisores

A propiedade estabelecida por Gauss para os divisores d dun número n di

$\sum _{d\mid n}\varphi (d)=n$.

.

A inversión de Möbius aplicada á fórmula da suma do divisor dá

$\varphi (n)=\sum _{d\mid n}\mu \left(d\right)\cdot {\frac {n}{d}}=n\sum _{d\mid n}{\frac {\mu (d)}{d}},$

onde μ é a función de Möbius, función multiplicativa definida por $\mu (p)=-1$ e $\mu (p^{k})=0$ para cada primo p e k ≥ 2. Esta fórmula tamén se pode derivar da fórmula do produto realizando ese produto ${\textstyle \prod _{p\mid n}(1-{\frac {1}{p}})}$ para conseguir ${\textstyle \sum _{d\mid n}{\frac {\mu (d)}{d}}.}$

Un exemplo: $${\begin{aligned}\varphi (20)&=\mu (1)\cdot 20+\mu (2)\cdot 10+\mu (4)\cdot 5+\mu (5)\cdot 4+\mu (10)\cdot 2+\mu (20)\cdot 1\\[.5em]&=1\cdot 20-1\cdot 10+0\cdot 5-1\cdot 4+1\cdot 2+0\cdot 1=8.\end{aligned}}$$

Algúns valores

Os primeiros 100 valores (secuencia [[OEIS:{{{id}}}|{{{id}}}]] na OEIS) móstranse na táboa e no gráfico a continuación:

Gráfico dos 100 primeiros valores

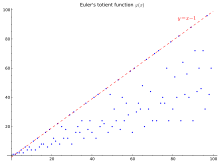
Na gráfica da dereita, a liña superior y = n − 1 é un límite superior válido para tódolos n distintos de 1, e acadado se e só se n é un número primo. Un límite inferior simple é $\varphi (n)\geq {\sqrt {n/2}}$, que é bastante lixeiro: de feito, o límite inferior da gráfica é proporcional a n/log log n

Teorema de Euler

Indica que se a e n son primos relativos, daqula

$a^{\varphi (n)}\equiv 1\mod n.$

O caso especial onde n é primo coñécese como pequeno teorema de Fermat.

Isto segue do teorema de Lagrange e do feito de que φ(n) é a orde do grupo multiplicativo de enteiros módulo n.

Outras fórmulas

• $a\mid b\implies \varphi (a)\mid \varphi (b)$
• $m\mid \varphi (a^{m}-1)$
• $\varphi (mn)=\varphi (m)\varphi (n)\cdot {\frac {d}{\varphi (d)}}\quad {\text{where }}d=\operatorname {gcd} (m,n)$ In particular:
  • $\varphi (2m)={\begin{cases}2\varphi (m)&{\text{ if }}m{\text{ is even}}\\\varphi (m)&{\text{ if }}m{\text{ is odd}}\end{cases}}$
  • $\varphi \left(n^{m}\right)=n^{m-1}\varphi (n)$
• $\varphi (\operatorname {lcm} (m,n))\cdot \varphi (\operatorname {gcd} (m,n))=\varphi (m)\cdot \varphi (n)$ Compare this to the formula ${\textstyle \operatorname {lcm} (m,n)\cdot \operatorname {gcd} (m,n)=m\cdot n}$ (see least common multiple).
• φ(n) is even for n ≥ 3. Moreover, if n has r distinct odd prime factors, 2^r | φ(n)
• For any a > 1 and n > 6 such that 4 ∤ n there exists an l ≥ 2n such that l | φ(aⁿ − 1).
• ${\frac {\varphi (n)}{n}}={\frac {\varphi (\operatorname {rad} (n))}{\operatorname {rad} (n)}}$ where rad(n) is the radical of <span about="#mwt315" class="texhtml mvar" data-cx="[{&quot;adapted&quot;:true,&quot;partial&quot;:false,&quot;targetExists&quot;:true,&quot;mandatoryTargetParams&quot;:[&quot;1&quot;],&quot;optionalTargetParams&quot;:[]}]" data-mw="{&quot;parts&quot;:[{&quot;template&quot;:{&quot;target&quot;:{&quot;wt&quot;:&quot;Mvar&quot;,&quot;href&quot;:&quot;./Modelo:Mvar&quot;},&quot;params&quot;:{&quot;1&quot;:{&quot;wt&quot;:&quot;n&quot;}},&quot;i&quot;:0}}]}" data-ve-no-generated-contents="true" id="mwAhw" style="font-style:italic;" typeof="mw:Transclusion">n</span> (the product of all distinct primes dividing n).
• $\sum _{d\mid n}{\frac {\mu ^{2}(d)}{\varphi (d)}}={\frac {n}{\varphi (n)}}$ 
• $\sum _{1\leq k\leq n-1 \atop gcd(k,n)=1}\!\!k={\tfrac {1}{2}}n\varphi (n)\quad {\text{for }}n>1$
• $\sum _{k=1}^{n}\varphi (k)={\tfrac {1}{2}}\left(1+\sum _{k=1}^{n}\mu (k)\left\lfloor {\frac {n}{k}}\right\rfloor ^{2}\right)={\frac {3}{\pi ^{2}}}n^{2}+O\left(n(\log n)^{\frac {2}{3}}(\log \log n)^{\frac {4}{3}}\right)$ ( cited in)
• $\sum _{k=1}^{n}\varphi (k)={\frac {3}{\pi ^{2}}}n^{2}+O\left(n(\log n)^{\frac {2}{3}}(\log \log n)^{\frac {1}{3}}\right)$ [Liu (2016)]
• $\sum _{k=1}^{n}{\frac {\varphi (k)}{k}}=\sum _{k=1}^{n}{\frac {\mu (k)}{k}}\left\lfloor {\frac {n}{k}}\right\rfloor ={\frac {6}{\pi ^{2}}}n+O\left((\log n)^{\frac {2}{3}}(\log \log n)^{\frac {4}{3}}\right)$ 
• $\sum _{k=1}^{n}{\frac {k}{\varphi (k)}}={\frac {315\,\zeta (3)}{2\pi ^{4}}}n-{\frac {\log n}{2}}+O\left((\log n)^{\frac {2}{3}}\right)$ 
• $\sum _{k=1}^{n}{\frac {1}{\varphi (k)}}={\frac {315\,\zeta (3)}{2\pi ^{4}}}\left(\log n+\gamma -\sum _{p{\text{ prime}}}{\frac {\log p}{p^{2}-p+1}}\right)+O\left({\frac {(\log n)^{\frac {2}{3}}}{n}}\right)$ (where γ is the Euler–Mascheroni constant).

Identidade de Menon

En 1965 P. Kesava Menon demostrou que

$\sum _{\stackrel {1\leq k\leq n}{\gcd(k,n)=1}}\!\!\!\!\gcd(k-1,n)=\varphi (n)d(n),$

onde d(n) = σ₀(n) é o número de divisores de n.

Funcións xeradoras

A serie de Dirichlet para φ(n) pódese escribir en termos da función zeta de Riemann como:

$\sum _{n=1}^{\infty }{\frac {\varphi (n)}{n^{s}}}={\frac {\zeta (s-1)}{\zeta (s)}}$

onde o lado esquerdo converxe para $\Re (s)>2$ .

A función xeradora da serie de Lambert é

$\sum _{n=1}^{\infty }{\frac {\varphi (n)q^{n}}{1-q^{n}}}={\frac {q}{(1-q)^{2}}}$

que converxe para |q| < 1.

Taxa de crecemento

Segundo as palabras de Hardy e Wright, a orde de φ(n) é "sempre case n".

Primeiro

$\lim \sup {\frac {\varphi (n)}{n}}=1,$

mais cando n vai ao infinito, para todo δ > 0

${\frac {\varphi (n)}{n^{1-\delta }}}\rightarrow \infty .$

Estas dúas fórmulas pódense probar usando pouco máis que as fórmulas para φ(n) e a función suma de divisores σ(n) .

De feito, durante a proba da segunda fórmula, próbase a desigualdade

${\frac {6}{\pi ^{2}}}<{\frac {\varphi (n)\sigma (n)}{n^{2}}}<1$.

Tamén temos que

$\lim \inf {\frac {\varphi (n)}{n}}\log \log n=e^{-\gamma }.$

Aquí γ é a constante de Euler-Mascheroni, γ = 0.577215665... , polo que e^γ = 1.7810724... e e^−γ = 0.56145948... .

Para a orde media, temos

$\varphi (1)+\varphi (2)+\cdots +\varphi (n)={\frac {3n^{2}}{\pi ^{2}}}+O\left(n(\log n)^{\frac {2}{3}}(\log \log n)^{\frac {4}{3}}\right)\quad {\text{as }}n\rightarrow \infty ,$

debido a Arnold Walfisz, a súa proba aproveita estimacións sobre sumas exponenciais debidas a I.M. Vinogradov e N.M. Korobov. Por unha combinación dos métodos de van der Corput e Vinogradov, H.-Q. Liu (Sobre a función de Euler.Proc. Roy. Soc. Edinburgh Sect. A 146 (2016), no 4, 769–775) mellorou o termo de erro a

$O\left(n(\log n)^{\frac {2}{3}}(\log \log n)^{\frac {1}{3}}\right)$

(esta é actualmente a estimación máis coñecida deste tipo). A notación "O grande" representa unha cantidade que está limitada por unha constante multiplicada pola función de n dentro dos parénteses (que é pequena en comparación con n²).

Este resultado pódese usar para demostrar que a probabilidade de que dous números escollidos aleatoriamente sexan coprimos é 6/π², que é a recíproca da zeta de Riemann de 2, igual a $1/\zeta (2)$.

Ratio de valores consecutivos

En 1950 Somayajulu demostrou

${\begin{aligned}\lim \inf {\frac {\varphi (n+1)}{\varphi (n)}}&=0\quad {\text{and}}\\[5px]\lim \sup {\frac {\varphi (n+1)}{\varphi (n)}}&=\infty .\end{aligned}}$

En 1954 Schinzel e Sierpiński reforzaron isto, demostrando que o conxunto

$\left\{{\frac {\varphi (n+1)}{\varphi (n)}},\;\;n=1,2,\ldots \right\}$

é denso nos números reais positivos. Tamén demostraron que o conxunto

$\left\{{\frac {\varphi (n)}{n}},\;\;n=1,2,\ldots \right\}$

é denso no intervalo (0,1).

Números totientes

Un número totiente é un valor da función totiente de Euler: é dicir, un m para o cal hai polo menos un n para o cal φ(n) = m . A valencia ou multiplicidade dun número totiente m é o número de solucións desa ecuación. Un número non totiente é un número natural que non é un número totiente. Todo número enteiro impar que exceda 1 é trivialmente un non totiente. Tamén hai infinitos non totientes pares, e de feito cada número enteiro positivo ten un múltiplo que é un non tociente par.

O número de números totientes ata un límite dado x é

${\frac {x}{\log x}}e^{{\big (}C+o(1){\big )}(\log \log \log x)^{2}}$

para unha constante C = 0.8178146....

Se se conta segundo a multiplicidade, o número de números totientes ata un determinado límite x é

${\Big \vert }\{n:\varphi (n)\leq x\}{\Big \vert }={\frac {\zeta (2)\zeta (3)}{\zeta (6)}}\cdot x+R(x)$

onde o termo de erro R é de orde como máximo

Aplicacións

Ciclotomía

Na última sección das Disquisitiones Gauss demostra que un n-gono regular pode construírse con regra e compás se φ(n) é unha potencia de 2. Se n é unha potencia dun número primo impar, a fórmula para o totiente di que o seu totiente pode ser unha potencia de dous só se n é unha primeira potencia e n − 1 é unha potencia de 2. Os primos que son un máis que unha potencia de 2 chámanse primos de Fermat e só se coñecen cinco: 3, 5, 17, 257 e 65537. Fermat e Gauss sabían destes. Ninguén puido demostrar se hai máis.

Así, un n-gono regular ten unha construción con escadro e compás se n é un produto de distintos números primos de Fermat e calquera potencia de 2. Os primeiros n son

2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30, 32, 34, 40,... (secuencia [[OEIS:{{{id}}}|{{{id}}}]] na OEIS) .

O criptosistema RSA

Configurar un sistema RSA implica escoller grandes números primos p e q, calcular n = pq e k = φ(n) e atopar dous números e e d tal que ed ≡ 1 (mod k). Os números n e e (a "chave de cifrado") son liberados ao público, e d (a "chave de descifrado") mantense en privado.

Unha mensaxe, representada por un número enteiro m, onde 0 < m < n, encriptase calculando S = m^e (mod n).

Descífrase calculando t = S^d (mod n). O teorema de Euler pódese usar para demostrar que se 0 < t < n, daquela t = m .

A seguridade dun sistema RSA veríase comprometida se o número n puidese factorizarse eficientemente ou se φ(n) puidese calcularse eficientemente sen factorizar n.

Problemas sen resolver

Conxectura de Lehmer

Se p é primo, daquela φ(p) = p − 1. En 1932 D. H. Lehmer preguntou se hai números compostos n tal que φ(n) divide a n − 1. Non se coñece ningún.

En 1933 demostrou que se existe algún n dese tipo, debe ser impar, libre de cadrados e divisíbel por polo menos sete números primos (é dicir, ω(n) ≥ 7 ). En 1980 Cohen e Hagis demostraron que n > 10²⁰ e que ω(n) ≥ 14. Alén diso, Hagis demostrou que se 3 divide n logo n > 10^1937042 e ω(n) ≥ 298848 .

A conxectura de Carmichael

Di que non hai un número n coa propiedade de que para todos os demais números m, m ≠ n, φ(m) ≠ φ(n).

Como se indica no artigo principal, se hai un único contraexemplo para esta conxectura, debe haber infinitos contraexemplos, e o máis pequeno ten polo menos dez mil millóns de díxitos en base 10.

Hipótese de Riemann

A hipótese de Riemann é certa se e só se a desigualdade

${\frac {n}{\varphi (n)}}<e^{\gamma }\log \log n+{\frac {e^{\gamma }(4+\gamma -\log 4\pi )}{\sqrt {\log n}}}$

é certa para todos os n ≥ p₁₂₀₅₆₉# onde γ é a constante de Euler-Macheroni e p₁₂₀₅₆₉# é o produto dos primeiros 120569 primos.

Véxase tamén

Bibliografía

• Abramowitz, M.; Stegun, I. A. (1964). Handbook of Mathematical Functions. New York: Dover Publications. ISBN 0-486-61272-4. . See paragraph 24.3.2.
• Bach, Eric; Shallit, Jeffrey (1996). Algorithmic Number Theory (Vol I: Efficient Algorithms). MIT Press Series in the Foundations of Computing. Cambridge, MA: The MIT Press. ISBN 0-262-02405-5. Zbl 0873.11070. 
• Dickson, Leonard Eugene, "History Of The Theory Of Numbers", vol 1, chapter 5 "Euler's Function, Generalizations; Farey Series", Chelsea Publishing 1952
• Ford, Kevin (1999). The number of solutions of φ(x) = m. Annals of Mathematics 150. pp. 283–311. ISSN 0003-486X. JSTOR 121103. MR 1715326. Zbl 0978.11053. doi:10.2307/121103. .
• Gauss, Carl Friedrich (1986). Disquisitiones Arithmeticae (Second, corrected edition). Traducido por Clarke, Arthur A. New York: Springer. ISBN 0-387-96254-9. 
• Gauss, Carl Friedrich (1965). Untersuchungen uber hohere Arithmetik (Disquisitiones Arithmeticae & other papers on number theory) (Second edition). Traducido por Maser, H. New York: Chelsea. ISBN 0-8284-0191-8. 
• Graham, Ronald; Knuth, Donald; Patashnik, Oren (1994). Concrete Mathematics: a foundation for computer science (2nd ed.). Reading, MA: Addison-Wesley. ISBN 0-201-55802-5. Zbl 0836.00001. 
• Guy, Richard K. (2004). Unsolved Problems in Number Theory. Problem Books in Mathematics (3rd ed.). New York, NY: Springer-Verlag. ISBN 0-387-20860-7. Zbl 1058.11001. 
• Hardy, G. H.; Wright, E. M. (1979). An Introduction to the Theory of Numbers (Fifth ed.). Oxford: Oxford University Press. ISBN 978-0-19-853171-5. 
• Liu, H.-Q. (2016). On Euler’s function. Proc. Roy. Soc. Edinburgh Sect. A 146. .
• Long, Calvin T. (1972). Elementary Introduction to Number Theory (2nd ed.). Lexington: D. C. Heath and Company. LCCN 77-171950. 
• Pettofrezzo, Anthony J.; Byrkit, Donald R. (1970). Elements of Number Theory. Englewood Cliffs: Prentice Hall. LCCN 77-81766. 
• Ribenboim, Paulo (1996). The New Book of Prime Number Records (3rd ed.). New York: Springer. ISBN 0-387-94457-5. Zbl 0856.11001. 
• Sandifer, Charles (2007). The early mathematics of Leonhard Euler. MAA. ISBN 978-0-88385-559-1. 
• Sándor, József; Mitrinović, Dragoslav S.; Crstici, Borislav, eds. (2006). Handbook of number theory I. Dordrecht: Springer-Verlag. pp. 9–36. ISBN 1-4020-4215-9. Zbl 1151.11300. 
• Sándor, Jozsef; Crstici, Borislav (2004). Handbook of number theory II. Dordrecht: Kluwer Academic. pp. 179–327. ISBN 1-4020-2546-7. Zbl 1079.11001. 
• Schramm, Wolfgang (2008). The Fourier transform of functions of the greatest common divisor. Electronic Journal of Combinatorial Number Theory A50. .

Outros artigos

• Función de Carmichael| (λ)
• Función psi de Dedekind (𝜓)
• Función divisor (σ)

• Conxectura de Duffin–Schaeffer
• Pequeno teorema de Fermat
• Número altamente composto
• Grupo multiplicativo de enteiros módulo n
• Suma de Ramanujan
• Función sumatoria totiente (𝛷)

Ligazóns externas

• "Totient function". Encyclopedia of Mathematics. EMS Press. 2001 [1994]. 
• Euler's Phi Function and the Chinese Remainder Theorem — proof that φ(n) is multiplicative Arquivado 2021-02-28 en Wayback Machine.
• Euler's totient function calculator in JavaScript — up to 20 digits
• Dineva, Rosica, The Euler Totient, the Möbius, and the Divisor Functions Arquivado 2021-01-16 en Wayback Machine.
• Plytage, Loomis, Polhill Summing Up The Euler Phi Function