Xeometría proxectiva

En matemáticas, a xeometría proxectiva é a rama que estuda as propiedades de incidencia das figuras xeométricas, pero abstraéndose totalmente do concepto de medida. A miúdo úsase esta palabra tamén para falar da teoría da proxección chamada xeometría descritiva.

Historia[editar | editar a fonte]

Ilustración de A. Bosse do *Tratado* de Desargues.

As primeiras propiedades xeométricas de natureza proxectiva foron descubertas durante o século III por Pappus de Alexandría. Filippo Brunelleschi (1404–1472) comezou a investigar a xeometría da perspectiva en 1425^[1]

Gérard Desargues é o iniciador da xeometría proxectiva, pois fundamentou matematicamente os métodos da perspectiva que desenvolveran os artistas do Renacemento, e aínda que o seu traballo foi publicado en 1639, pasou desapercibido durante dous séculos (excepto dous teoremas), ensombrecido pola influente obra de Descartes.

No século XIX establecéronse dentro das matemáticas a xeometría proxectiva e a xeometría hiperbólica, pero o que acabou de enraizalas, posiblemente, foi achar un modelo analítico. Dentro do contexto da xeometría euclidiana-cartesiana pódese construír a xeometría proxectiva e, se se acepta a primeira, hai que admitir a segunda.

Este proceso finalizou definitivamente a principios do século XX, pois Einstein, apoiándose nos exhaustivos desenvolvementos xeométricos dos matemáticos do século XIX, conseguiu demostrar que, a grande escala, o universo se pode interpretar mellor con estas novas xeometrías que co ríxido espazo euclidiano.

Punto de vista sintético[editar | editar a fonte]

Desde o punto de vista sintético, a xeometría proxectiva é unha xeometría que parte dos seguintes principios:

Dous puntos definen unha recta.
Todo par de rectas córtanse nun punto (cando dúas rectas son paralelas dicimos que se cortan nun punto do infinito coñecido como punto impropio).

O quinto postulado de Euclides, das rectas paralelas, está implícito nestes dous principios xa que, dada unha recta e un punto exterior, existirá unha única recta paralela definida polo punto dado e o do infinito polo primeiro axioma.

Como os axiomas dos que se parte son simétricos, se en calquera teorema proxectivo se intercambian as palabras recta e punto obtense outro teorema igualmente válido. A estes teoremas chámaselles duais.

O principio antes exposto coñécese como principio de Dualidade e foi enunciado por Poncelet no século XIX. Moitos teoremas anteriores, como os de Pascal e Brianchon, son duais, aínda que ningún matemático o notara até entón.

Os teoremas de Pascal e Brianchon, aínda que completamente válidos, demostráronse inicialmente en xeometría euclidiana, baseándose nos teoremas de Pappus e Menelao, que utilizan unha métrica e polo tanto non son válidos en xeometrías de incidencia, como a proxectiva.

En principio tentouse buscar demostracións alternativas destes teoremas sen usar congruencia de segmentos. Hilbert demostrou en 1899 que tal cousa é imposible e desde entón adoita incluírse o teorema do hexágono de Pappus como un axioma da xeometría proxectiva. Iso permite demostrar en proxectiva todo o demostrable en euclidiana sen ter que recorrer a unha métrica.

Por non usar métricas nos seus enunciados, dise que a xeometría proxectiva é unha xeometría de incidencia.

Finalmente, hai que destacar que dende o punto de vista sintético, un espazo proxectivo consiste nun espazo afín ao que se engade un conxunto de puntos infinitos, de modo que cada par de rectas paralelas se cortan nun destes puntos.

Aplicacións[editar | editar a fonte]

Cando facemos isomorfas as paralelas euclidianas coas rectas proxectivas que se cortan "no infinito", pódese extrapolar todo o que se demostre en proxectiva á xeometría euclidiana. A xeometría proxectiva, máis flexible que a euclidiana, convértese con isto nunha ferramenta útil para enunciar moitos teoremas clásicos máis sinxelamente, e mesmo simplificar as demostracións, aínda que non permite demostrar nada que non poida demostrarse na euclidiana.

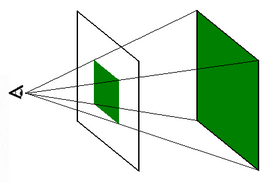
A xeometría proxectiva pode entenderse, informalmente, como a xeometría que se obtén cando nos colocamos nun punto, mirando desde ese punto. Isto é, calquera liña que incide no noso "ollo" parécenos ser só un punto, no plano proxectivo, xa que o ollo non pode "ver" os puntos que hai detrás.

Desta forma, a xeometría proxectiva tamén equivale á proxección sobre un plano dun subconxunto do espazo na xeometría euclidiana tridimensional. As rectas que chegan ao ollo do observador proxéctanse en puntos. Os planos definidos por cada par delas proxéctanse en rectas.

Isto é útil porque ás veces os teoremas de xeometría proxectiva non poden demostrarse só cos axiomas de incidencia antes expostos (Hilbert, 1899) e é necesario demostralos en xeometría euclidiana e logo proxectar, como o teorema de Desargues (ou ben admitir o teorema de Pappus anteriormente citado como axioma).

Punto de vista vectorial[editar | editar a fonte]

A xeometría proxectiva é o estudo do grupo das proxectividades entre espazos proxectivos.

Axiomas[editar | editar a fonte]

Sexa $K$ un corpo e $V$ un $K$ -espazo vectorial (non trivial).

Definida en $E-\{0\}\,$ a seguinte relación de equivalencia: $x\sim y\Leftrightarrow \exists \lambda \in K^{*},x=\lambda y\,$ .

Chámase espazo proxectivo sobre $V$ ao conxunto cociente de $V-\{0\}\,$ pola relación de equivalencia anterior $\sim$ :

P(V)=(V-\{0\})/\sim \,\!

.

As rectas vectoriais de $V$ son conxuntos formados polos múltiplos escalares dos vectores non nulos, isto é, se $v\in V$ , $v\neq 0$ , a recta vectorial determinada por $v$ é o conxunto $\{\lambda v:\lambda \in K,\lambda \neq 0\}$ . A recta vectorial determinada por $v$ non é entón outra cousa que o subespazo vectorial xerado por $v$ , é dicir, $L(v)$ . O espazo proxectivo $P(V)$ asociado a $V$ será o conxunto de todas as rectas vectoriais de $V$ .

É inmediato que se $v\in V$ , $v\neq 0$ , entón para calquera $u\in V$ tal que $u=\beta v$ con $\beta \neq 0$ , cúmprese que as rectas vectoriais determinadas por $u$ e por $v$ coinciden, isto é, $\{\lambda v:\lambda \in K\}$ = $\{\alpha u:\alpha \in K\}$ . Aí reside a esencia dun espazo proxectivo: considéranse só as direccións, non os vectores concretos. Ante este feito, para traballar só con vectores e non con rectas vectoriais, establécese a seguinte relación, que resulta ser unha relación de equivalencia: se $u,v\in V\setminus \{0\}$ , dise que $u$ está relacionado con $v$ (escríbese como $uRv$ ) se existe un $\lambda \in K$ de maneira que $v=\lambda u$ . Ao tomar o conxunto cociente $V/R$ obtense outra forma de definir $P(V)$ .

Os elementos do espazo proxectivo serían entón as clases de equivalencia dos vectores de $V$ mediante a relación de equivalencia $R$ .

Aínda pode darse outro paso máis para comprender mellor este tipo de espazos: se se toma unha base de $V$ , como ao tomar a recta vectorial xerada por $v$ esíxese que $v\neq 0$ , algunha das coordenadas de $v$ respecto da base tomada ten que ser necesariamente non nula. Ao multiplicar escalarmente o vector non nulo polo inverso desa coordenada non nula obterase outro vector da mesma recta vectorial, no que agora a coordenada non nula escollida vai valer 1. Como o novo vector está na mesma recta vectorial, a súa clase de equivalencia é a mesma que a do vector antigo, é dicir, representa o mesmo elemento do espazo proxectivo.

Exemplo[editar | editar a fonte]

A continuación exponse nun exemplo que significa isto:

Tómese o espazo vectorial real $\mathbb {R} ^{5}$ (coa base canónica) e o vector non nulo $(8,{\frac {\pi }{3}},0,2^{-15},{\sqrt {7}})$ .

Denótase por $[(8,{\frac {\pi }{3}},0,2^{-15},{\sqrt {7}})]$ a súa clase de equivalencia mediante a relación $R$ . Catro das cinco coordenadas son non nulas, así que temos catro posibles maneiras de realizar o proceso anterior: no primeiro caso (dividindo entre a primeira coordenada, o 8) obteríase $[(1,{\frac {\pi }{24}},0,2^{-18},{\frac {\sqrt {7}}{8}})]$ . Se en lugar de tomar a primeira coordenada tómase, por exemplo, a quinta ( ${\sqrt {7}}$ ), obteríase $[({\frac {8}{\sqrt {7}}},{\frac {\pi }{3{\sqrt {7}}}},0,{\frac {2^{-15}}{\sqrt {7}}},1)]$ . Poderíase dividir as coordenadas do vector inicial $(8,{\frac {\pi }{3}},0,2^{-15},{\sqrt {7}})$ entre as outras dúas coordenadas non nulas, ${\frac {\pi }{3}}$ ou $2^{-15}$ , pero en todos os casos obteríase a mesma clase de equivalencia, aínda que as coordenadas non sexan numericamente as mesmas. Nesta situación dirase que $(8:{\frac {\pi }{3}}:0:2^{-15}:{\sqrt {7}})$ é a representación da clase do vector $(8,{\frac {\pi }{3}},0,2^{-15},{\sqrt {7}})$ en coordenadas homoxéneas. Cómpre salientar que $(8:{\frac {\pi }{3}}:0:2^{-15}:{\sqrt {7}})$ , $(1:{\frac {\pi }{24}}:0:2^{-18}:{\frac {\sqrt {7}}{8}})$ e $({\frac {8}{\sqrt {7}}}:{\frac {\pi }{3{\sqrt {7}}}}:0:{\frac {2^{-15}}{\sqrt {7}}}:1)$ son coordenadas homoxéneas do mesmo punto proxectivo.