Espiral logarítmica

Unha espiral logarítmica, equiangular ou de crecemento é unha clase de curva que aparece frecuentemente na natureza. O seu nome provén da expresión dunha das súas ecuacións:
Historia
[editar | editar a fonte]O termo espiral logarítmica débese a Pierre Varignon. Foi estudada por Descartes e Torricelli e Jakob Bernoulli, chamouna Spira mirabilis «a espiral marabillosa». D'Arcy Thompson dedicoulle un capítulo do seu tratado On Growth and Form ("Sobre crecemento e forma", 1917).
Bernoulli escolleu a espiral logarítmica como emblema, e o epitafio en latín Eadem mutata resurgo (Mutante e permanente, volvo rexurdir sendo o mesmo) para a súa tumba; contrariamente ao seu desexo de que fose tallada unha espiral logarítmica (constante no crecemento do seu raio), a espiral que tallaron os mestres canteiros na súa tumba foi unha espiral de Arquímedes (constante na diferenza dos raios).[1] A logarítmica distínguese polo feito de que as distancias entre os seus brazos se incrementan en progresión xeométrica, mentres na espiral de Arquímedes esas distancias son constantes.
Ecuacións
[editar | editar a fonte]
En coordenadas polares (, ) a fórmula é
ou ben
- , de aquí o nome "logarítmica"
e en forma paramétrica
con números reais positivos e .
é un factor de escala que determina o tamaño da espiral, mentres controla canto e en que dirección está enrolada. Para a espiral expándese cun incremento θ, e para contráese.
En xeometría diferencial, a espiral pode definirse como unha curva cun ángulo constante α entre o raio e o vector tanxente
Se α = 0 a espiral logarítmica dexenera nunha liña recta.
Se a espiral logarítmica dexenera nunha circunferencia.
Características
[editar | editar a fonte]
Calquera liña recta á orixe cortará a espiral logarítmica co mesmo ángulo α, que pode calcularse (en radiáns) como .
O grao da espiral é o ángulo (constante) que a espiral posúe con circunferencias centradas na orixe. Pode calcularse como . Unha espiral logarítmica de grao 0 () é unha circunferencia; o caso límite é unha espiral logarítmica de grao 90 ( ou ) é unha liña recta desde a orixe.
Comezando nun punto e movéndose cara a dentro, ao longo da espiral, hai que rodear a orixe infinitas veces antes de alcanzalo; con todo, a distancia total deste camiño é finita. O primeiro en darse conta disto foi Torricelli mesmo antes de que se idease o cálculo infinitesimal. A distancia total é , onde é a distancia en liña recta desde á orixe.
Pódense construír espirais logarítmicas de grao 17,03239 utilizando a sucesión de Fibonacci ou a proporción áurea.
Outro cálculo mostra que a lonxitude do arco entre a orixe e o punto da espiral é proporcional a . O coeficiente de proporcionalidade é igual á raíz cadrada de . Se α é o ángulo no que a espiral corta os raios, este coeficiente de proporcionalidade é, polo tanto, igual a . Desta propiedade dedúcese o seguinte fenómeno: se se fai rodar unha espiral logarítmica sobre a súa tanxente, o centro da espiral móvese sobre unha liña.
Espirais logarítmicas na natureza
[editar | editar a fonte]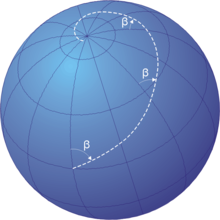
Os brazos das galaxias espirais son aproximadamente espirais logarítmicas. A Vía Láctea crese que ten catro brazos espirales maiores, cada un dos cales sería unha espiral logarítmica duns 12 graos.
Os brazos dos ciclóns tropicais, como os furacáns, tamén forman espirais logarítmicas.
En bioloxía son frecuentes as estruturas aproximadamente iguais á espiral logarítmica. Por exemplo, as teas de araña e as cunchas de molusco. A razón é a seguinte: comeza cunha figura irregular F0. Auméntase F0 nun certo factor para obter F1, e ponse F1 xunto a F0 de forma que se toquen dous lados. Auméntase F1 no mesmo factor para obter F2, e ponse xunto a F1 , como antes. Repetindo este proceso xérase aproximadamente unha espiral logarítmica cuxo grao está determinado polo factor de expansión e o ángulo con que as figuras son postas unha á beira doutra.
O falcón aproxímase á súa presa segundo unha espiral logarítmica: a súa mellor visión está en ángulo coa súa dirección de voo; este ángulo é o mesmo que o grao da espiral.
Os insectos aproxímanse ás luces artificiais segundo unha espiral aproximadamente logarítmica, porque están afeitos voar cun ángulo constante ás fontes luminosas. Normalmente son o Sol ou a Lúa a única fonte de luz e voar desta forma produce un voo en liña recta, xa que o insecto non fai voos tan longos como para que a posición do Sol ou a Lúa cambie significativamente.
En xeotecnia, a superficie de falla é o lugar xeométrico dos puntos onde o chan "rompe" e permite un deslizamento, ao estar sometido a cargas maiores á que pode soportar. Estas superficies de falla en moitos casos son iguais ou aproximábeis a unha espiral logarítmica.
Tamén nos xirasoles se atopan repetidas espirais logarítmicas.
Galería
[editar | editar a fonte]-
Tumba de Bernoulli en Basilea, onde gravaron outra espiral (non a logarítmica que el pedira)
-
Fracción dun fractal Mandelbrot.
-
Fracción do fractal "cabalo de mar"
-
Imaxe da Galaxia de Bode (M81) polo Telescopio Espacial Spitzer, na que se pode observar po interestelar seguindo aproximadamente unha espiral logarítmica.
-
Galaxia M51 polo Telescopio Hubble. Os brazos achéganse á espiral logarítmica
-
Ciclón Catarina, un infrecuente ciclón tropical do Atlántico Sur visto desde a Estación Espacial Internacional. Ten uns uns brazos que se aproximan á forma dunha espiral logarítmica.
-
Unha borrasca sobre Islandia. O patrón que segue aproxímase á forma dunha espiral logarítmica.
-
Corte da cuncha dun nautilus onde se aprecian as cámaras formando aproximadamente unha espiral logarítmica.
-
Detalle dun xirasol, a distribución das sementes achégase a unha espiral logarítmica.
-
O símbolo de Debian parécese a unha espiral logarítmica.
-
Escadas do Vaticano, construída con espirais logarítmicas.
Notas
[editar | editar a fonte]Véxase tamén
[editar | editar a fonte]| Wikimedia Commons ten máis contidos multimedia na categoría: Espiral logarítmica |
Outros artigos
[editar | editar a fonte]- Espiral
- Espiral de Fermat
- Espiral de Ulam
- Espiral hiperbólica
- Fractal
- Número áureo
- Pentagrama (xeometría)
- Número e
Ligazóns externas
[editar | editar a fonte]- https://www.youtube.com/watch?v=zfNTaAVBgIk Vídeo da construción xeométrica da espiral.
- http://jsxgraph.uni-bayreuth.de/wiki/index.php/Logarithmic_spiral Exploración online en JSXGraph (JavaScript)



































