Triángulo de Pascal

O triángulo de Pascal, tamén coñecido como triángulo de Tartaglia, é un triángulo de números enteiros, infinito e simétrico.
Fundamentos[editar | editar a fonte]
Constrúese do seguinte xeito: Empézase polo « 1 » do cume. Dunha liña á seguinte convense escribir os números cun desfasamento de media casa. Así, as casas (que non se debuxan) terán cada unha dúas casas xusto encima, na liña anterior. O valor que se escribe nunha casa é a suma dos valores das dúas casas enriba dela. O valor cero non se escribe. Por exemplo, na última liña debuxada, o cuarto valor é 84 = 28 + 56, suma do terceiro e cuarto valor da liña anterior. Obsérvase, e non é difícil demostralo, que a capa exterior está formada de uns, a segunda capa dos naturais en orde crecente, que os números non fan máis que subir dunha liña á seguinte e que existe un eixo de simetría vertical que pasa polo vértice.
Con todo, o interese deste triángulo non radica nestas propiedades, senón no vínculo que ten co álxebra elemental. En efecto, as cifras 1; 2; 1 e 1; 3; 3; 1 recordan as identidades:
| y |
pois son os coeficientes dos seus monomios. Este parecido non é casual e xeneralízase a calquera potencia do binomio a + b.
Relación entre o triángulo de Pascal e o binomio de Newton[editar | editar a fonte]
A fórmula que dá o desenvolvemento de segundo as potencias crecentes de a (e decrecientes de b) chámase binomio de Newton. Nesta expresión, o único que se descoñece son os coeficientes dos monomios .
Teorema
Os coeficientes da forma desenvolvida de (a + b)n son dados
pola liña número n+1 do triángulo de Pascal (a que empeza por 1 e n).
Proba
Xa está visto que é certo para n=2 e n=3. Tamén o é para n=0.
Para establecer o resultado para calquera valor de n ∈ ℕ, o máis natural é proceder por indución.
Supondo que é certo para un valor de n, hai que deducir que o é tamén para n+1. No canto de facelo no caso xeral (sería pouco claro) miremos que sucede ao pasar da liña n = 3 á liña n = 4.
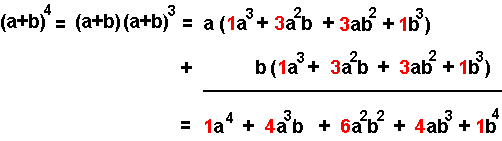
Como o mostra a figura, o desenvolvemento de (a + b)4 consiste en dúas copias do desenvolvemento de (a + b)³. Están desfasadas (unha corresponde a a⋅(a + b)³ e a outra a b⋅(a + b)³) e cando se suman, un mesmo coeficiente aparece nunha posición dada e outra vez a un paso á dereita.
Se se considera só os coeficientes, inscritos en sendas casas, obtemos a suma seguinte:

e obviamente non fai falta escribir dúas veces as mesmas cifras: a suma consiste en engadir a un coeficiente o coeficiente inmediatamente á súa dereita (o 1 co 3, o 3 co segundo 3 etc) e isto é xustamente o que se fai no triángulo de Pascal. Noutras palabras, o triángulo simula a multiplicación de (a + b), dunha liña á seguinte.
Coeficientes do binomio de Newton[editar | editar a fonte]

Inscríbese o triángulo de Pascal nunha táboa para poder nomear a cada coeficiente do mesmo. O número na liña n e a columna p denótase:
| ou máis raramente |
("C" por "combinación") (por exemplo en calculadoras de peto, como a TI-86 e familia), e dise "n sobre k", "combinación de n en k" moito máis curto que "coeficiente binomial n, k". As casas baleiras corresponden a valores nulos. Por definición mesma, temos, (para todo n natural):
para calquera valor de a e b. De feito, é unha igualdade de polinomios en ℤ[a, b]. Sen perder en xeneralidade, resulta ás veces máis práctica a "definición" :
vista como unha igualdade de polinomios en ℤ[X]. Desta fórmula dedúcense dúas consecuencias:
| Tomando X = 1 obtense: |
A suma dos coeficientes dunha mesma liña vale 2n. En efecto: 1 = 20, 1 + 1 =2= 2¹, 1 + 2 + 1 =4= 2², 1 + 3 + 3 + 1 =8= 2³, 1 + 4 + 6 + 4 + 1 =16= 24 ... · Con X = -1 obtense, (n > 0):
| : a suma alterna dos números dunha mesma liña vale 0. |
En efecto: 1 - 1 = 0, 1 - 2 + 1 = 0, 1 - 3 + 3 - 1 = 0, 1 - 4 + 6 - 4 + 1 = 0, 1 - 5 + 10 - 10 + 5 - 1 = 0 ... As propiedades que observamos no triángulo pódense agora escribir con todo rigor:
| . |
| (costados esquerdos e dereitos do triángulo). |
| . |
| ("segunda capa"). |
| . |
| (simetría respecto ao eixo vertical do triángulo). |
| . |
| cando p > n (corresponde á zona fose do triángulo). |
E claro, a regra de construción do triángulo dá a relación fundamental dos coeficientes binomiais:
| . |
Interpretación en combinatoria[editar | editar a fonte]
Os coeficientes binomiais son a base mesma da combinatoria. Vexamos por que: Tomemos de novo un binomio, por exemplo , e desarollémoslo, pero dun xeito distinto do parágrafo anterior:
logo quitemos #o\\\ #paréntese\\, pero sen cambiar a orde nos produtos, é dicir sen aplicar a conmutatividade:
E agrupemos os termos que conteñen o mesmo número de a, (e de b):
A primeira paréntese contén todas as palabras constituídas dun b e dous a. Neste caso, é fácil ver que hai exactamente tres. No caso xeral, para contar as palabras, hai que aplicar a conmutatividade, pois as palabras que conteñen o mesmo número da e b darán o mesmo termo:
| O primeiro factor 3, que é | conta as tres palabras mencionadas (aab, aba e baa). |
| O segundo factor 3, que é | conta as palabras feitas de dúas b e un a (abb, bab e bba). |
Obviamente, só hai unha palabra de tres letras constituídas de a soamente, e isto corresponde ao monomio 1·a³, con 1 = ( «0 » por ningunha b).
No canto de falar de palabras formadas con a e b, é equivalente imaxinar unha fileira de n caixóns inicialmente baleiros, e p bólas intercambiables que se teñen que repartir, en cada caixón non cabendo máis dunha. Trátase en todos casos de repartir p obxectos entre n sitios posibles, ou de escoller un grupo de p obxectos/sitios entre n obxectos/sitios. De aí a apelación p entre n.
Todo o anterior leva ao teorema:
| Hai exactamente | xeitos de escoller un conxunto de p elementos entre n elementos. |
En matemática formal, prefírese falar de conxuntos:
| Existen | subconjuntos de cardinal p nun conxunto de cardinal n. |
Este punto de vista permite achar a fórmula para os coeficientes binomiais. En efecto, para elixir o « primeiro » elemento, hai n posibilidades, logo para escoller o segundo quedan n-1 posibilidades e así sucesivamente ata o elemento número p, que ten n-p+1. A orde no que se elixiu estes p elementos non importa, podíase obter o mesmo subconjunto de p elementos noutra orde. Hai p! permutacións posibles destes p elementos, é dicir p! xeitos de obter o mesmo conxunto.
| Xa que logo hai | subconjuntos posibles. |
En conclusión:
| Verifiquémoslo nun exemplo: |
No triángulo, o valor na quinta liña e segunda columna é 10. Para rematar, listemos as palabras de cinco letras formadas de 2 a e 5-2 = 3 b (na orde alfabética, ou na orde crecente considerando que a é a cifra 0 e b a cifra 1):
aabbb, ababb, abbab, abbba, baabb, babab, babba, bbaab, bbaba, bbbaa.
A fórmula permite verificar todas as propiedades do parágrafo anterior, con todo pódese prescindir dos cálculos na maioría dos casos, con tal de manipular os conceptos idóneos.
Un subconjunto A de E define unha partición de E en dous partes E = A B ∪ , coa ∩ B = {}= ∅ (conxunto baleiro). Aquí é o complementario da en E.
Dá o mesmo escoller os p elementos da que os n-p elementos de math .
| Isto xustifica, sen cálculo, a simetría | . |
| Se > p n, non hai subconjuntos de E con p elementos, porque E contén só n, logo |
| Tamén son evidentes as igualdades | e | porque, no primeiro caso, |
hai tantos xeitos de escoller subconjunto de tamaño 1 que de elementos de E, e no segundo caso, só existe un conxunto con cero elemento: o conxunto baleiro.
A regra fundamental tamén ten explicación gráfica:
Proba: escóllese un elemento e calquera de E, que contén n+1 elementos: E = E' ∪ {e}. Logo considéranse os subconjuntos A de E de cardeal p+1. Son de dous tipos: ou conteñen e, ou non.
| Se e ∈ A, entón falta elixir p elementos de E' para completar A. Hai | posibilidades. |
| Se e ∉ A, entón falta elixir p+1 elementos de E' para definir A. Hai | posibilidades. |
Sumando os dous casos, obtense todos as partes de p+1 elementos de E, constituído de n+1 elementos.
| Hai xa que logo |
Un exemplo:
Aquí vai unha propiedade aritmética, sen interpretación xeométrica: cando n é primo, os coeficientes binomiais na liña n son divisibles por n, excepto os dous bordos da mesma (que valen 1). Escrito formalmente:
| Teorema : |

Na figura, os exemplos están en verde, e os contraejemplos (cando n non é primo e p divide n) en amarelo.
| Proba: na fracción | o factor primo |
n aparece unha vez no numerador e xamais no denominador. (O denominador é un produto de números entre 1 e n-1). Xa que logo a fracción é divisible por n.
Xeneralización[editar | editar a fonte]
No canto de considerar as potencias de a + b, pódese mirar as do trinomio a + b + c.
(a + b + c)n é unha suma de monomios da forma λp, q, r
·a sup<>p·bq·cr, con p, q e r positivos, p + q + r = n, e λp, q, r un natural que se tería que chamar coeficiente trinomial.
Os cálculos son similares aos do coeficiente binomial, e dan a expresión seguinte:
Corresponde ao número de partición en tres dun conxunto de n elementos, en subconjuntos de p, q e r elementos. Un exemplo:

Estes coeficientes pódense achar na analogía tridimensional do triángulo de Pascal: Poderíase chamar a pirámide de Pascal, é tamén infinita, con seccións triangulares, e o valor en cada casa é a suma dos valores das tres casas encima dela.
Debuxouse as primeiras seccións a partir do cume.
Obsérvase unha invariance por rotación de 120 graos ao redor dun eixo vertical que pasa polo vértice.
O triángulo de Pascal aparece nas tres caras da pirámide.
Está claro que todo isto pódese xeneralizar a calquera dimensión finita, pero sen a posibilidade de facer debuxos explicativos.





































![{\displaystyle \forall p\in [1;n-1],n/{n \choose p}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d0bb050f7921a9637054c6308bc149dabbd27df)

