Resonancia orbital

Na mecánica celeste, unha resonancia orbital acontece cando dous corpos que orbitan a outro teñen unha influencia gravitacional regular polo que os seus períodos orbitais están relacionados nunha razón fracción de números enteiros simple. A resonancia orbital aumenta a influencia gravitatoria mutua, e na meirande parte dos casos non existe unha interacción inestable (a cal deixaría de ser resoante co tempo ao mudar o impulso e as órbitas). Noutros casos a resonancia estabilízase e autocorríxese, permanecendo os corpos na resonancia. Exemplos de resonancia son a 1:2:4 (número de órbitas completado no mesmo intervalo de tempo) das lúas de Xúpiter Ganímedes, Europa e Io; e a resonancia 2:3 entre Plutón e Neptuno (Plutón completa 2 órbitas no tempo en que Neptuno completa 3). Exemplo de resonancia inestable son as lúas de Saturno. Caso especial de resonancia 1:1 (que produce grandes corpos orbitantes) son as órbitas dos planetas xigantes do sistema solar, que sobreviviron ao expulsar os demais obxectos orbitantes ao Sol na zona da súa órbita arredor do Sol, efecto utilizado para a definición actual de planeta.

Historia

Dende o descubrimento da lei de Newton da gravitación universal no século XVII, a estabilidade do sistema solar ten preocupado a moitos matemáticos, a partir de Laplace. As órbitas estables que xorden na aproximación de dous corpos ignora a influencia doutros corpos. O efecto engadido destas interaccións a estabilidade do Sistema Solar e moi pequeno, pero non se sabía se se podería agregar ao longo de períodos mais extensos para modificar de xeito significativo os parámetros orbitais e conducir a unha configuración completamente diferente, ou se algún outro efecto estabilizador podería manter a configuración das órbitas dos planetas. Laplace atopou as primeiras respostas que explican o baile notable das lúas de Galileo. Este campo de estudo tense mantido moi activo dende entón, existindo moitas interaccións por resolver (p. ex., as interaccións das lúas cas partículas dos aneis dos planetas xigantes que permiten a subsistencia dos aneis).

Resonancia de Laplace

A resonancia de Laplace dos satélites de Xúpiter: Ganímedes, Europa e Ío

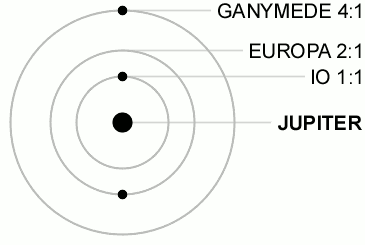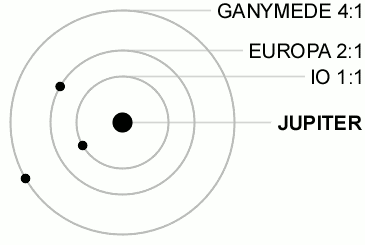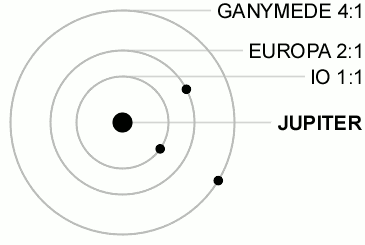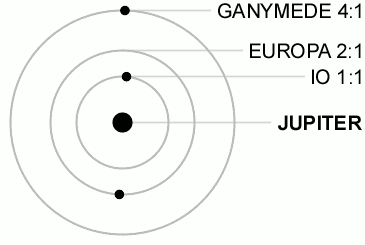
A resonancia mais coñecida e remarcable e a das tres lúas Galileanas, inclúe a relación que limita a posición das lúas nas súas órbitas:

$\Phi _{L}=\lambda _{Io}-3\cdot \lambda _{Eu}+2\cdot \lambda _{Ga}=180^{o}$

onde $\lambda$ son as lonxitudes medias das lúas. Esta restrición fai imposible unha tripla conxunción das lúas.

Véxase tamén

Outros artigos

• Puntos de Lagrange
• Rotación síncrona
• Lei de Titius-Bode