Distribución de Poisson
Función de masa de probabilidade | |
Función de distribución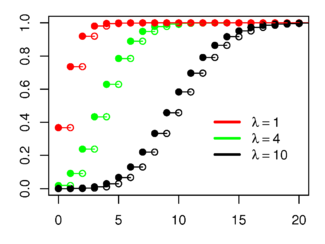 | |
| Parámetros | |
| Soporte | |
| Función de densidade | |
| Función de distribución | (onde é a función gamma incompleta) |
| Media | |
| Mediana | [1] |
| Moda | |
| Varianza | |
| Asimetría | |
| Curtose | |
| Entropía | |
| F. xeradora de momentos | |
| Func. caract. | |
A distribución de Poisson é unha distribución de probabilidade discreta que expresa, a partir dunha frecuencia de ocorrencia media, a probabilidade de que ocorra un determinado número de sucesos durante certo período de tempo. Concretamente, especialízase na probabilidade de que ocorran sucesos con probabilidades moi pequenas ou sucesos "raros".
Foi descuberta por Siméon-Denis Poisson, que a presentou en 1838 no seu traballo Recherches sur la probabilité des jugements en matières criminelles et matière civile (Investigación sobre a probabilidade dos xuízos en materias criminais e civís).
Propiedades
[editar | editar a fonte]A función de masa ou probabilidade de Poisson é
onde
- k é o número de veces que ocorre o fenómeno.
- λ é un parámetro positivo que representa o número de veces que se espera que suceda o fenómeno durante un intervalo dado. Por exemplo, se o suceso ten lugar unha media de catro veces por minuto e estamos interesados na probabilidade de que ocorra k veces nun intervalo de 10 minutos, empregaremos un modelo de distribución de Poisson con λ = 10×4 = 40.
- e é a base dos logaritmos naturais (e = 2,71828...)
Tanto o valor esperado como a varianza dunha variable aletoria con distribución de Poisson son iguais a λ. Os momentos de orde superior son polinomios de Touchard en λ con coeficientes que teñen unha interpretación combinatoria. De feito, cando o valor esperado da distribución de Poisson é 1, entón segundo a fórmula de Dobinski, o n-ésimo momento é igual ao número de particións de tamaño n.
A moda dunha variable aleatoria de distribución de Poisson con λ non enteiro é igual a , o maior dos enteiros menores que λ (os símbolos representan a función parte enteira). Cando λ é un enteiro positivo, as modas son λ e λ − 1.
A función xeradora de momentos da distribución de Poisson con valor esperado λ é
As variables aleatorias de Poisson teñen a propiedade de ser infinitamente divisibles.
A diverxencia de Kullback-Leibler dende unha variable aleatoria de Poisson de parámetro λ0 a outra de parámetro λ é
Intervalo de confianza
[editar | editar a fonte]Un criterio fácil e rápido para calcular un intervalo de confianza aproximado de λ foi proposto por Guerriero en 2012.[2] Dada unha serie de sucesos k (polo menos 15 ou 20) nun período de tempo T, os límites do intervalo de confianza para a frecuencia veñen dados por:
entón os límites do parámetro están dados por:.
Relación con outras distribucións
[editar | editar a fonte]Sumas de variables aleatorias de Poisson
[editar | editar a fonte]A suma de variables aleatorias de Poisson independentes é outra variable aleatoria de Poisson que ten como parámetro a suma dos parámetros das orixinais: se
son N variables aleatorias de Poisson independentes, entón
- .
Distribución binomial
[editar | editar a fonte]A distribución de Poisson é o caso límite da distribución binomial. De feito, se os parámetros n e dunha distribución binomial tenden a infinito (no caso de 'n') e a cero (no caso de ) de xeito que se manteña constante, a distribución límite obtida é de Poisson.
Aproximación normal
[editar | editar a fonte]Como consecuencia do teorema central do límite, para valores grandes de , unha variable aleatoria de Poisson X pode aproximarse por outra normal dado que o cociente
converxe a unha distribución normal de media nula e varianza 1.
Distribución exponencial
[editar | editar a fonte]Se para cada valor t > 0, que representa o tempo, o número de sucesos de certo fenómeno aleatorio segue unha distribución de Poisson de parámetro λt, entón os tempos transcorridos entre dous sucesos sucesivos segue a distribución exponencial.
Exemplos
[editar | editar a fonte]Se o 2% dos libros encadernados en certo taller ten encadernación defectuosa, para obter a probabilidade de que 5 de 400 libros encadernados neste taller teñan encadernacións defectuosas emprégase a distribución de Poisson. Neste caso concreto, k é 5 e, λ, o valor esperado de libros defectuosos é o 2% de 400, é dicir, 8. Polo tanto, a probabilidade buscada é
Procesos de Poisson
[editar | editar a fonte]A distribución de Poisson aplícase a diversos fenómenos discretos da natureza (aqueles fenómenos que ocorren 0, 1, 2, 3... veces durante un período definido de tempo ou nunha área determinada) cando a probabilidade de que ocorra o fenómeno é constante no tempo ou no espazo. Exemplos destes sucesos que poden ser analizados pola distribución de Poisson inclúen:
- O número de vehículos que pasan a través dun certo punto nunha ruta durante un período definido de tempo.
- O número de erros ortográficos que un comete ao escribir unha única páxina.
- O número de chamadas nunha central telefónica por minuto.
- O número servidores web accedidos por minuto.
- O número de mutacións dunha cadea de ADN determinada despois de certa cantidade de radiación.
- O número de núcleos atómicos inestables que se desintegraron nun determinado período.
- O número de estrelas nun volume do espazo.
- A distribución de receptores visuais na retina do ollo humano.
- As creacións dun inventor durante a súa carreira.[3]
- A distribución da riqueza humana.
Notas
[editar | editar a fonte]- ↑ Hamza, K. (1995). The smallest uniform upper bound on the distance between the mean and the median of the binomial and Poisson distributions. Statist. Probab. Lett. 23 21–25.
- ↑ Guerriero, V. "Power Law Distribution: Method of Multi-scale Inferential Statistics". J. Mod. Math. Fr.
- ↑ Huber, John C. (1998-7). "Invention and Inventivity Is a Random, Poisson Process: A Potential Guide to Analysis of General Creativity". Creativity Research Journal (en inglés) 11 (3): 231–241. ISSN 1040-0419. doi:10.1207/s15326934crj1103_3.









![{\displaystyle \lambda [1\!-\!\ln(\lambda )]\!+\!e^{-\lambda }\sum _{k=0}^{\infty }{\frac {\lambda ^{k}\ln(k!)}{k!}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24650c837524f593a60e41f7371b39de75512d5c)

















