Axiomas de Tarski

Os axiomas de Tarski, debidos a Alfred Tarski, son un conxunto de axiomas da parte substancial da xeometría euclidiana que é formulable en lóxica de primeira orde con identidade, e sen necesidade ningunha da teoría de conxuntos (por exemplo, aquela parte da xeometría euclidiana que é formulable como unha teoría elemental). Outros modelos de axiomatizacións da xeometría euclidiana son a dos axiomas de Hilbert e a dos axiomas de Birkhoff.

Xeneralidades[editar | editar a fonte]

Nos primeiros tempos da súa carreira Tarski ensinou xeometría e investigou a teoría de conxuntos. O seu compañeiro de traballo Steven Givant (1999) explicou o punto de vista de Tarski:

A través de Enriques, Tarski aprendeu do traballo de Mario Pieri, un xeómetra italiano que foi fortemente influído por Peano. Tarski preferiu o sistema de Pieri [da súa memoria Point and Sphere], onde a estrutura lóxica e a complexidade dos axiomas era máis transparente.

Givant entón di que "co rigor típico" Tarski argallou o seu sistema:

Que hai de diferente na aproximación de Tarski á xeometría? Primeiro de nada, o sistema axiomático era moito máis sinxelo que ningún dos outros sistemas existentes nese tempo. De feito o tamaño de todos os axiomas de Tarski xuntos non é moito máis que só un dos 24 axiomas de Pieri. Era o primeiro sistema da xeometría euclidiana que era o bastante sinxelo como para ser expresado en termos das nocións primitivas unicamente, sen a axuda de nocións definidas. De maior importancia é o feito de que por primeira vez foi feita unha distinción clara entre a xeometría completa e a parte elemental —isto é, a de primeira orde —.

Tal e como se fai noutras axiomatizacións modernas da xeometría euclidiana, Tarski emprega un sistema formal que consiste en cadeas de símbolos, chamadas sentenzas, cuxa construción respecta as regras sintácticas formais, e regras de demostración que determinan as manipulacións permitidas das sentenzas. A diferenza dalgunhas outras modernas axiomatizacións como a de Birkhoff e a de Hilbert, a axiomatización de Tarski non ten ningún outro obxecto primitivo mais que os puntos, así que unha variable ou unha constante non pode referirse a unha liña ou un ángulo. A razón de por que os puntos son os únicos obxectos primitivos é porque o sistema de Tarski é unha teoría de primeira orde, polo que nin tan sequera é posible definir as liñas como conxuntos de puntos. As únicas relacións primitivas (predicados) son "estar entre" e "congruencia" entre puntos.

A axiomatización de Tarski é máis curta que as dos seus rivais, nun sentido que Tarski e Givant (1999) fan explícito. É máis conciso que Pieri porque este tiña só dúas nocións primitivas mentres que Tarski presentou tres: punto, "estar entre" e congruencia. Tal economía de nocións primitivas definidas significa que o sistema de Tarski non é moi conveniente para facer xeometría euclidiana. Con todo, Tarski deseñou o seu sistema para facilitar a súa análise por medio das ferramentas da lóxica matemática, por exemplo para facilitar as derivacións das súas propiedades metamatemáticas. O sistema de Tarski ten a propiedade infrecuente de que todas as frases poden ser escritas mediante a forma existencial, un caso especial da forma normal prenexa. Esta forma escríbese con cuantificadores universais que preceden aos cuantificadores existenciais de modo que todas as frases poden ser reescritas da forma $\forall u\forall v\ldots \exists a\exists b\dots .$ Este feito permitiu a Tarski probar que a xeometría euclidiana é decidible: existe un algoritmo que pode determinar a verdade ou falsidade de calquera enunciado. A axiomatización de Tarski tamén é completa. Isto non contradí o primeiro teorema de incompletitude de Gödel, porque a teoría de Tarski carece do poder expresivo necesario para interpretar a aritmética de Robinson.(Franzén 2005, pp. 25–26)

Os axiomas[editar | editar a fonte]

Alfred Tarski traballou na axiomatization das metatemáicas da xeometría euclidiana intermitentemente desde 1926 até a súa morte en 1983, con el mesmo (1959) anunciando o seu interese maduro no asunto. O traballo de Tarski e os seus estudantes na xeometría euclidiana culminou na monografía de Schwabhäuser, Szmielew e Tarski (1983), na que estableceu dez axiomas e o esquema de axioma mostrados abaixo, as metamatemáticas asociadas, e algo do tema. Gupta (1965) fixo contribucións importantes, e Tarski e Givant (1999) trataron a historia.

Relacións fundamentais[editar | editar a fonte]

Estes axiomas son unha versión máis elegante dun conxunto ideado por Tarski na década de 1920 como parte da súa investigación das propiedades metamatemáticas da xeometría plana euclidiana. Este obxectivo necesitou unha reformulación da xeometría como unha teoría de primeira orde. Tarski fíxoo postulando un universo de puntos, con minúsculas denotando as variábeis que varían sobre ese universo. A igualdade é proporcionada pola lóxica subxacente.^[1]

Tarski entón postulou dúas relacións primitivas:

"Situado ente", unha relación triádica. A frase atómica Bxyz denota que y está "entre" x e z, noutras palabras, que y é un punto no segmento de recta xz. (Esta relación é interpretada inclusivamente de modo que Bxyz é trivialmente certo cando x=y ou y=z).
"Congruencia" (ou "equidistancia"), unha relación tetrádica. A frase atómica wx ≡ yz pode ser interpretada como wx é congruente con yz, noutras palabras, que a lonxitude do segmento de recta wx é igual á lonxitude do segmento de liña yz.

A relación "estar entre" captura o aspecto afín da xeometría euclidiana; a congruencia, o seu aspecto métrico. A lóxica de fondo inclúe identidade, unha relación binaria. Os axiomas invocan a identidade (ou a súa negación) en cinco ocasións.

Os axiomas agrúpanse polo tipo de relación que invocan, ordenados, primeiro polo número de cuantificadores existenciais, despois polo número de sentenzas atómicas. Os axiomas débense ler como conclusións universais; por iso as variables libres terían que ser tomadas tacitamente como cuantificadores universais.

Axiomas de congruencia[editar | editar a fonte]

Reflexividade da congruencia: $xy\equiv yx\,.$
Identidade da congruencia: $xy\equiv zz\rightarrow x=y.$
Transitividade da congruencia: $(xy\equiv zu\land xy\equiv vw)\rightarrow zu\equiv vw.$

Mentres a relación de congruencia $xy\equiv zw$ é, formalmente, unha relación entre 4 puntos, tamén pode ser pensada, informalmente, como unha relación binaria entre dous segmentos lineares $xy$ e $zw$ . Os axiomas de reflexividade e de transitividade combinados proban:

Esta relación binaria é unha relación de equivalencia
- É reflexiva: $xy\equiv xy$
- É simétrica: $xy\equiv zw\rightarrow zw\equiv xy$
- É transitiva: $(xy\equiv zu\land zu\equiv vw)\rightarrow xy\equiv vw$
e a orde na que os puntos dun segmento son especificados é irrelevante.
- $xy\equiv zw\rightarrow xy\equiv wz$
- $xy\equiv zw\rightarrow yx\equiv zw$
- $xy\equiv zw\rightarrow yx\equiv wz$

O axioma de transitividade afirma que a congruencia é euclidiana, polo que respecta a primeira das "nocións comúns" de Euclides.

O axioma da identidade da congruencia establece, intuitivamente, que se xy é congruente cun segmento que empeza e finaliza no mesmo punto, entón x e y son o mesmo punto. Isto está estreitamente relacionado coa noción de reflexividade para relacións binarias.

Axiomas de ordenación[editar | editar a fonte]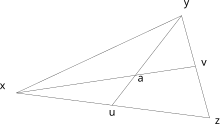

Identidade na relación "situado entre": $Bxyx\rightarrow x=y.$ . O único punto no segmento de liña $xx$ é o propio $x$
Axioma de Pasch: $Bxyz\lor Byzx\lor Bzxy\lor \exists a\,(xa\equiv ya\land xa\equiv za)$ . As dúas diagonais do cuadrilátero $xuvy$ teñen que cortarse nalgún punto.

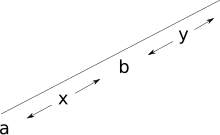
Esquema de axioma de continuidade:

Sexan φ(x) e ψ(y) fórmulas de primeira orde que non conteñan ningún caso libre de ningún a ou b. Tampouco haberá ningún caso libre de x en ψ(y) ou de y en φ(x). Entón tense o seguinte esquema de axioma: $\exists a\,\forall x\,\forall y\,[(\phi (x)\land \psi (y))\rightarrow Baxy]\rightarrow \exists b\,\forall x\,\forall y\,[(\phi (x)\land \psi (y))\rightarrow Bxby].$

Sexa r unha semirecta con punto inical a. Sexan as fórmulas de primeira orde φ e ψ definindo subconxuntos X e Y de r, tales que cada punto en Y está á dereita de cada punto de X (con respecto a un punto a). Entón existe un punto b en r entre X e Y. Isto é esencialmente a construción do corte de Dedekind, levado a cabo nun xeito que evita cuantificación sobre conxuntos.

Dimensión máis baixa: $\exists a\,\exists b\,\exists c\,[\neg Babc\land \neg Bbca\land \neg Bcab]$ . Existen tres puntos non colineares. Sen este axioma, a teoría podería ser modelada pola liña real unidimensional, un único punto, ou mesmo o conxunto baleiro.

Congruencia a a relación "estar entre"[editar | editar a fonte]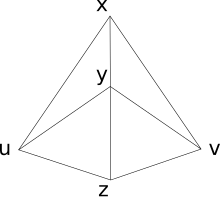

Dimensión superior: $(xu\equiv xv\land yu\equiv yv\land zu\equiv zv\land u\neq v)\rightarrow (Bxyz\lor Byzx\lor Bzxy).$

Tres puntos equidistantes doutros dous puntos distintos forman unha liña. Sen este axioma, a teoría podería ter un modelo tridimensional ou dunha maior dimensión espacial.

Axioma de Euclides

Cada unha das tres variantes deste axioma, todas equivalentes xunto cos restantes axiomas de Tarski, ao postulado das paralelas de Euclides, ten unha vantaxe sobre os outros, a variante A non ten cuantificadores existenciais; a variante B ten o menor número de variables e de sentenzas atómicas; e a variante C require unicamente dunha noción primitiva, "estar entre". Esta variante é a habitualmente dada na literatura:

A:

((Bxyw\land xy\equiv yw)\land (Bxuv\land xu\equiv uv)\land (Byuz\land yu\equiv zu))\rightarrow yz\equiv vw.

Sexa un segmento de liña que une o punto medio de dous lados dun triángulo dado. Ese segmento de recta será como moito a metade do terceiro lado. Isto é equivalente a que a suma dos ángulos interiores de calquera triángulo sexa igual a dous ángulos rectos.

B:

(Bxuv\land Byuz\land x\neq u)\rightarrow \exists a\,\exists b\,(Bxya\land Bxzb\land Bavb).

Dado calquera triángulo, existe unha circunferencia que pasa por todos os seus vértices.

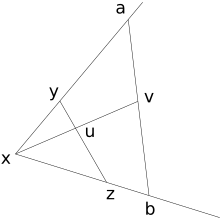
C:

{(x\neq y\land Bxyz\land Bx'y'z'\land xy\equiv x'y'\land yz\equiv y'z'\land xu\equiv x'u'\land yu\equiv y'u')}\rightarrow zu\equiv z'u'.

Dado un ángulo calquera e un punto calquera v no seu interior, existe un segmento de recta que contén a v, cun punto en cada lado do ángulo.

Cinco segmentos: ${(x\neq y\land Bxyz\land Bx'y'z'\land xy\equiv x'y'\land yz\equiv y'z'\land xu\equiv x'u'\land yu\equiv y'u')}\rightarrow zu\equiv z'u'.$

Comézase con dous triángulos, xuz e x'u'z'. Debúxanse os segmentos de recta yu e y'u', conectando un vértice de cada triángulo a un punto do oposto ao vértice. O resultado son dous triángulos divididos, cada un formado por cinco segmentos. Se catro segmentos dun dos triángulos son congruentes a cada segmento no outro triángulo, entón os quintos segmentos en ambos os dous triángulos teñen que ser congruentes.

Isto é equivalente á regra do lado-ángulo-lado para determinar que dous triángulos son congruentes; se os ángulos uxz e u'x'z' son congruentes (existen triángulos congruentes xuz e x'u'z'), e os dous pares de lados incidentes son congruentes (xu ≡ x'u' e xz ≡ x'z'), entón o par restante de lados é tamén congruente (uz ≡ u'z').

Construción de segmento: $\exists z\,[Bxyz\land yz\equiv ab]$ . Para calquera punto y, é posible debuxar en calquera dirección (determinado por x) unha liña congruente a calquera segmento ab.

Discusión[editar | editar a fonte]

A partir de dúas relacións primitivas cuxos campos son un universo denso de puntos, Tarski construíu unha xeometría de segmentos de liña. Segundo Tarski e Givant (1999: 192-93), ningún dos axiomas dados arriba é fundamentalmente novo. Os primeiro catro axiomas estabelecen algunhas propiedades elementais das dúas relacións primitivas. Para o caso, a reflexividade e a transitividade da congruencia estabelecen que a congruencia é unha relación de equivalencia sobre segmentos de liña. A Identidade da congruencia e a relación "estar entre" establece o caso trivial cando aquelas relacións son aplicadas a puntos non distintos. O teorema xy≡zz ↔ x=y ↔ Bxyx estende eses axiomas de identidade.

Algunhas das outras propiedades da relación "estar entre" son derivables como teoremas incluíndo:

Reflexividade: Bxxy ;
Simetría: Bxyz → Bzyx ;
Transitividade: (Bxyw ∧ Byzw) → Bxyz ;
Conectividade: (Bxyw ∧ Bxzw) → (Bxyz ∨ Bxzy).

As últimas dúas propiedades ordenan totalmente os puntos formando un segmento de liña.

Os axiomas de dimensión superior e de dimensión inferior xuntos establecen que calquera modelo destes axiomas terá unha dimensión específica finita. Cambios adecuados nestes axiomas dan lugar a conxuntos de axiomas da xeometría eucidiana para dimensións 0, 1 e máis grande que 2.^[2] Decátese de que xeometría sólida non require novos axiomas, a diferenza do caso dos axiomas de Hilbert. Ademais, a máis baixa dimensión para a dimensión n é simplemente a negación da dimensión superior para a dimensión n - 1.

Cando o número de dimensións é máis grande que 1, a relación "estar entre" pode ser definida en termos de congruencia.^[3] Primeiro defínese a relación "≤" (onde $ab\leq cd$ é interpretado como "a lonxitude de segmento $ab$ é menor ou igual á lonxitude de segmento $cd$ "):

xy\leq zu\leftrightarrow \forall v(zv\equiv uv\rightarrow \exists w(xw\equiv yw\land yw\equiv uv)).

No caso de dúas dimensións, a intuición é como segue: Para calquera segmento de liña xy, considerar o rango de posibles lonxitudes xv, onde v é calquera punto na mediatriz de xy. É evidente que mentres non hai un límite superior da lonxitude xv, hai un límite inferior, o cal ocorre cando v é o punto medio de xy. Así que se xy é máis curto ou igual a zu, entón o rango de lonxitudes posibles de xv será sempre superio ao rango de lonxitudes posibles de zw, onde w é calquera punto na perpendicular bisector de zu.

A relación "estar entre" pode ser definida usando a intuición de que a distancia máis curta entre dous puntos é unha liña recta:

Bxyz\leftrightarrow \forall u((ux\leq xy\land uz\leq zy)\rightarrow u=y).

O esquema de axiomas de continuidade asegura que a ordenación dos puntos nunha liña é completa (con respecto ás propiedades definibles de primeira orde). Os axiomas de Pasch e de Euclides son ben coñecidos. Extraordinariamente, a xeometría euclidiana require só o seguinte axioma adicional:

Construción dun segmento. Este axioma asegura o establecemento dunha medida e o sistema de coordenadas cartesianas —simplemente atribuíndo o valor de 1 a algún segmento de liña arbitrario e non baleiro; ^{[Cómpre clarificar]}

Escribamos wff para identificar unha fórmula ben formada (ou fórmula correcta sintaticamente) da xeometría elemental. Tarski E Givant (1999: 175) probaron que a xeometría elemental é:

Consistente: Non hai wff tales que ela e a súa negación son ambas teoremas;
Completo: Cada sentenza ou a súa negación é un teorema que se pode probar a partir dos axiomas;
Decidible: Existe un algoritmo que atribúe un valor de verdade a cada sentenza. Disto séguese, por Tarski que:
- Procedemento de decisión para o corpo pechado real, que el encontrou por eliminación dos cuantificadores (o teorema de Tarski–Seidenberg);
- Os axiomas admiten unha interpretación multidimensional fiel como corpo pechado real.

Gupta (1965) probou a independencia dos axiomas citados arriba agás o de Pasch e o da reflexividade da congruencia.

A negación do axioma de Euclides leva á xeometría hiperbólica, mentres que eliminándoo obtense a xeometría absoluta. A xeometría euclidiana completa (en oposición á elemental) require ir máis alá da axiomatization de primeira orde: substitúe φ(x) e ψ(y) no esquema de axioma de continuidade con x ∈ A e y ∈ B, onde A e B son variables cuantificadas universalmente que varían sobre conxuntos de puntos.

Comparación con Hilbert[editar | editar a fonte]

Os axiomas de Hilbert para o plano son un total de 16, e inclúen a transitividade da congruencia e unha variante do axioma de Pasch. A única noción invocada desde a xeometría intuitiva invocada nos comentarios aos axiomas de Tarski é a de triángulo. (As versións B e C do axioma de Euclides refírense a "círculo" e "ángulo," respectivamente.) Os axiomas de Hilbert tamén requiren as nocións de "raio", "ángulo," e a dun triángulo que "inclúe" un ángulo. Alén da relación "estar entre" e a congruencia, os axiomas necesitan a relación binaria "encima," vinculando un punto e unha liña. O esquema de axiomas da continuidade xoga unha función similar aos dous axiomas de continuidade de Hilbert. Este esquema é indispensable; a xeometría euclidiana na linguaxe deTarski (ou equivalente) non pode ser finitamente axiomatizada como teoría de primeira orde. Os axiomas de Hilbert non constitúen unha teoría de primeira orde porque os seus axiomas de continuidade requiren da lóxica de segunda orde.

Os primeiros catro grupos de axiomas de Hilbert para xeometría plana son bi-interpretables cos axiomas de Tarski agás a continuidade.

Notas[editar | editar a fonte]

↑ Tarski e Givant, 1999, page 177
↑ Tarski e Givant 1999: Axioms 8⁽¹⁾, 8⁽ⁿ⁾, 9⁽⁰⁾, 9⁽¹⁾, 9⁽ⁿ⁾
↑ Tarski e Givant, 1999

Véxase tamén[editar | editar a fonte]

Bibliografía[editar | editar a fonte]

Franzén, Torkel (2005). Gödel's Theorem: An Incomplete Guide to Its Use and Abuse. A K Peters. ISBN 1-56881-238-8.
Givant, Steven (1999) "Unifying threads in Alfred Tarski's Work", Mathematical Intelligencer 21:47–58.
Gupta, H. N. (1965) Contributions to the Axiomatic Foundations of Geometry. Ph.D. thesis, University of California-Berkeley.
Tarski, Alfred (1959). "What is elementary geometry?". En Leon Henkin, Patrick Suppes and Alfred Tarski. The axiomatic method. With special reference to geometry and physics. Proceedings of an International Symposium held at the Univ. of Calif., Berkeley, Dec. 26, 1957-Jan. 4, 1958. Studies in Logic and the Foundations of Mathematics. Amsterdam: North-Holland. pp. 16–29. MR 0106185. . Available as a 2007 reprint, Brouwer Press, ISBN 1-4437-2812-8
Tarski, Alfred; Givant, Steven (1999). Tarski's system of geometry. The Bulletin of Symbolic Logic 5. pp. 175–214. ISSN 1079-8986. JSTOR 421089. MR 1791303. doi:10.2307/421089.
Schwabhäuser, W., Szmielew, W., e Alfred Tarski, 1983. Metamathematische Methoden in der Geometrie. Springer-Verlag.

Outros artigos[editar | editar a fonte]

[1] Tarski e Givant, 1999, page 177

[2] Tarski e Givant 1999: Axioms 8⁽¹⁾, 8⁽ⁿ⁾, 9⁽⁰⁾, 9⁽¹⁾, 9⁽ⁿ⁾

[3] Tarski e Givant, 1999

[1]

[2]

[3]