Saltar ao contido

Sólido arquimediano

Na Galipedia, a Wikipedia en galego.

Os sólidos arquimedianos son un grupo de poliedros convexos con caras que son polígonos regulares de dous ou máis tipos. Todos os sólidos de Arquímedes son de vértices uniformes. A maioría deles obtense truncando os sólidos platónicos. Arquímedes describiu amplamente estes corpos en traballos que foron desaparecendo, e non foi ata o Renacemento cando artistas e matemáticos os redescubriron.

Construción

[editar | editar a fonte]

Sete sólidos arquimedianos poden obterse truncando sólidos platónicos: o tetraedro truncado, o cuboctaedro, o cubo truncado, o octaedro truncado, o icosidodecaedro, o dodecaedro truncado e o icosaedro truncado.

Os dous rombicuboctaedros poden obterse a partir do cuboctaedro mediante sucesivas operacións de truncamento e desprazamento radial das caras.

De forma similar, os dous rombicosidodecaedros poden obterse a partir do icosidodecaedro mediante sucesivas operacións de truncamento e desprazamento radial das caras.

As dúas formas isomórficas do cuboctaedro romo poden obterse a partir do rombicuboctaedro menor mediante unha transformación máis complexa que inclúe unha rotación coordinada dos cadrados paralelos aos orixinais do cubo, dous triángulos que os conectan polos seus vértices e, simultaneamente, a conversión de cada un dos cadrados que os conectan polas arestas en dous triángulos equiláteros. O sentido da rotación dos cadrados determina o isomorfismo do sólido resultante.

De forma similar, as dúas formas isomórficas do icosidodecaedro romo poden obterse a partir do rombicosidodecaedro menor mediante unha rotación coordinada dos pentágonos paralelos aos orixinais do dodecaedro, dos triángulos que os conectan polos seus vértices e, simultaneamente, a conversión de cada un dos cadrados que os conectan polas arestas en dous triángulos equiláteros. O sentido da rotación dos pentágonos determina o isomorfismo do sólido resultante.

O cuboctaedro é o caso límite coincidente do truncamento do cubo e do octaedro. De forma similar, o icosidodecaedro é o caso límite coincidente do truncamento do dodecaedro e do icosaedro. Ambos son os únicos sólidos arquimedianos con arestas uniformes, polo que se consideran sólidos semirregulares.

Clasificación

[editar | editar a fonte]

A configuración dos vértices refírese ao tipo de polígonos regulares que concorren nun vértice dado. Por exemplo, se a configuración (4,6,8) significa que nun vértice se atopan un cadrado, un hexágono e un octógono coa orde en sentido das agullas do reloxo. Este sistema aplícase tamén para as demais familias de poliedros.

Nome
(Nomes alternativos) 		Schläfli
Coxeter 		Transparente Sólido Rede Configuración dos vértices Faces Arestas Vert. Volume Grupo de puntos Esfericidade
tetraedro truncado t{3,3}
 Truncated tetrahedron
(Animation) 		3.6.6
 8 4 triángulos
4 hexágonos 		18 12 2.710576 Td 0.7754132
cuboctaedro
(rombitetratetraedro)		 r{4,3} ou rr{3,3}
ou 		Cuboctahedron
(Animation) 		3.4.3.4
 14 8 triángulos
6 cadrados 		24 12 2.357023 Oh 0.9049973
cubo truncado t{4,3}
 Truncated hexahedron
(Animation) 		3.8.8
 14 8 triángulos
6 octógonos 		36 24 13.599663 Oh 0.8494937
octaedro truncado
(tetratetraedro truncado)		 t{3,4} ou tr{3,3}
ou 		Truncated octahedron
(Animation) 		4.6.6
 14 6 cadrados
8 hexágonos 		36 24 11.313709 Oh 0.9099178
rombicuboctaedro
(pequeno rombicuboctaedro)		 rr{4,3}
 Rhombicuboctahedron
(Animation) 		3.4.4.4
 26 8 triángulos
18 cadrados 		48 24 8.714045 Oh 0.9540796
cuboctaedro truncado
(gran rombicuboctaedro)		 tr{4,3}
 Truncated cuboctahedron
(Animation) 		4.6.8
 26 12 cadrados
8 hexágonos
6 octógonos 		72 48 41.798990 Oh 0.9431657
cubo romo
(cuboctaedro romo)		 sr{4,3}
 Snub hexahedron (Ccw)
(Animation) 		3.3.3.3.4
 38 32 triángulos
6 cadrados 		60 24 7.889295 O 0.9651814
icosidodecaedro r{5,3}
 Icosidodecahedron
(Animation) 		3.5.3.5
 32 20 triángulos
12 pentágonos 		60 30 13.835526 Ih 0.9510243
dodecaedro truncado t{5,3}
 Truncated dodecahedron
(Animation) 		3.10.10
 32 20 triángulos
12 decágonos 		90 60 85.039665 Ih 0.9260125
icosaedro truncado t{3,5}
 Truncated icosahedron
(Animation) 		5.6.6
 32 12 pentágonos
20 hexágonos 		90 60 55.287731 Ih 0.9666219
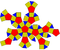
rombicosidodecaedro
(pequeno rombicosidodecaedro)		 rr{5,3}
 Rhombicosidodecahedron
(Animation) 		3.4.5.4
 62 20 triángulos
30 cadrados
12 pentágonos 		120 60 41.615324 Ih 0.9792370
icosidodecaedro truncado
(gran rombicosidodecaedro)		 tr{5,3}
 Truncated icosidodecahedron
(Animation) 		4.6.10
 62 30 cadrados
20 hexágonos
12 decágonos 		180 120 206.803399 Ih 0.9703127
dodecaedro romo
(icosidodecaedro romo)		 sr{5,3}
 Snub dodecahedron (Ccw)
(Animation) 		3.3.3.3.5
 92 80 triángulos
12 pentágonos 		150 60 37.616650 I 0.9820114

Algunhas definicións de poliedros semirregulares inclúen unha ou máis destas figuras, como a xirobicópula cadrada elongada ou o pseudo-rombicuboctaedro".[1]

Notas

[editar | editar a fonte]
  1. ↑ (Malkevitch 1988), p. 85

Véxase tamén

[editar | editar a fonte]

Bibliografía

[editar | editar a fonte]
  • Grünbaum, Branko (2009). An enduring error. Elemente der Mathematik 64. pp. 89–101. MR 2520469. doi:10.4171/EM/120. 
  • Jayatilake, Udaya (March 2005). "Calculations on face and vertex regular polyhedra". Mathematical Gazette 89 (514): 76–81. 
  • Malkevitch, Joseph (1988). "Milestones in the history of polyhedra". En Senechal, M.; Fleck, G. Shaping Space: A Polyhedral Approach. Boston: Birkhäuser. pp. 80–92. 
  • Pugh, Anthony (1976). Polyhedra: A visual approach. California: University of California Press Berkeley. ISBN 0-520-03056-7.  Chapter 2
  • Sutton, Daud (2005). Sólidos platónicos y arquimedianos. Oniro S. A. ISBN 84-9754-131-6. 

Outros artigos

[editar | editar a fonte]

Ligazóns externas

[editar | editar a fonte]
Traído desde «https://gl.wikipedia.org/w/index.php?title=Sólido_arquimediano&oldid=6872865»