Posición (xeometría)

En xeometría, unha posición ou vector de posición, é un vector euclidiano que representa un punto P no espazo. A súa lonxitude representa a distancia en relación a unha orixe de referencia arbitraria O, e a súa dirección representa a orientación angular con respecto a eixes de referencia dados. Normalmente denotado por x, r ou s, corresponde ao segmento de recta de O a P. Noutras palabras, é o desprazamento que asigna a orixe a P:

\mathbf {r} ={\overrightarrow {OP}}.

O termo vector de posición úsase principalmente nos campos da xeometría diferencial, mecánica e ocasionalmente cálculo vectorial.

Posición relativa

A posición relativa dun punto Q con respecto ao punto P é o vector euclidiano resultante da resta dos dous vectores de posición absoluta (cada un respecto á orixe):

\Delta \mathbf {r} =\mathbf {s} -\mathbf {r} ={\overrightarrow {PQ}},

onde $\mathbf {s} ={\overrightarrow {OQ}}$ .

A dirección relativa entre dous puntos é a súa posición relativa normalizada como un vector unitario:

\Delta \mathbf {\hat {r}} =\Delta \mathbf {r} /\|\Delta \mathbf {r} \|,

onde o denominador é a distancia entre os dous puntos, $\|\Delta \mathbf {r} \|$ . Unha dirección relativa é un vector ligado, en contraste cunha dirección ordinaria, que é un vector libre.

Definición e representación

En tres dimensións

En tres dimensións, pódese usar calquera conxunto de coordenadas tridimensionais e os seus correspondentes vectores de base para definir a localización dun punto no espazo; pódese utilizar o que sexa o máis sinxelo para a tarefa que se está a realizar.

Comunmente, úsase o sistema de coordenadas cartesiano, ou ás veces coordenadas polares esféricas ou coordenadas cilíndricas:

{\begin{aligned}\mathbf {r} (t)&\equiv \mathbf {r} (x,y,z)\equiv x(t)\mathbf {\hat {e}} _{x}+y(t)\mathbf {\hat {e}} _{y}+z(t)\mathbf {\hat {e}} _{z}\\&\equiv \mathbf {r} (r,\theta ,\phi )\equiv r(t)\mathbf {\hat {e}} _{r}{\big (}\theta (t),\phi (t){\big )}\\&\equiv \mathbf {r} (r,\phi ,z)\equiv r(t)\mathbf {\hat {e}} _{r}{\big (}\phi (t){\big )}+z(t)\mathbf {\hat {e}} _{z},\\\end{aligned}}

onde t é un parámetro, debido á súa simetría rectangular ou circular. Estas diferentes coordenadas e os correspondentes vectores de base representan o mesmo vector de posición. No seu lugar pódense usar coordenadas curvilíneas máis xerais e están en contextos como a mecánica de continuos e a relatividade xeral (neste último caso necesítase unha coordenada temporal adicional).

n dimensións

A álxebra linear permite a abstracción dun vector de posición n-dimensional. Un vector de posición pódese expresar como unha combinación linear de vectores de unha base: ^[1]^[2]

\mathbf {r} =\sum _{i=1}^{n}x_{i}\mathbf {e} _{i}=x_{1}\mathbf {e} _{1}+x_{2}\mathbf {e} _{2}+\dotsb +x_{n}\mathbf {e} _{n}.

Derivadas

Cantidades cinemáticas dunha partícula clásica: masa m, posición r, velocidade v, aceleración a

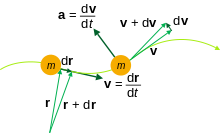
Para un vector de posición r que é función do tempo t, podemos calcular as derivadas en relación ao tempo t. Estas derivadas teñen unha utilidade común no estudo da cinemática, a teoría do control, enxeñaría e outras ciencias.

Velocidade: $\mathbf {v} ={\frac {\mathrm {d} \mathbf {r} }{\mathrm {d} t}},$; onde d r é un desprazamento infinitesimalmente pequeno.
Aceleración: $\mathbf {a} ={\frac {\mathrm {d} \mathbf {v} }{\mathrm {d} t}}={\frac {\mathrm {d} ^{2}\mathbf {r} }{\mathrm {d} t^{2}}}.$
Sobreaceleración ou arrincada: $\mathbf {j} ={\frac {\mathrm {d} \mathbf {a} }{\mathrm {d} t}}={\frac {\mathrm {d} ^{2}\mathbf {v} }{\mathrm {d} t^{2}}}={\frac {\mathrm {d} ^{3}\mathbf {r} }{\mathrm {d} t^{3}}}.$