Subgrupo

Na teoría de grupos, unha rama das matemáticas, dado un grupo G baixo unha operación binaria ∗, un subconxunto H de G chámase subgrupo de G se H tamén forma un grupo baixo a operación ∗. Máis precisamente, H é un subgrupo de G se a restrición de ∗ a H × H é unha operación de grupo en H. Isto denótase tamén como H ≤ G, lido como "H é un subgrupo de G ".

O subgrupo trivial de calquera grupo é o subgrupo {e} que consiste só no elemento identidade.

Un subgrupo propio dun grupo G é un subgrupo H que é un subconxunto propio de G (é dicir, H ≠ G). Isto represéntase por H < G, lido como "H é un subgrupo propio de G". Algúns autores tamén exclúen que o grupo trivial sexa propio (é dicir, H ≠ {e }).

Comprobación de subgrupos

Temos que G é un grupo e H é un subconxunto de G e a operación de grupo de G escríbese multiplicativamente.

• Daquela H é un subgrupo de G se e só se H non é baleiro e é pechado baixo produtos e inversos. Pechado baixo produtos significa que para cada a e b en H, o produto ab está en H. Pechado baixo inversos significa que para cada a en H, o inverso a⁻¹ está en H. Estas dúas condicións pódense combinar nunha soa, que para cada a e b en H, o elemento ab⁻¹ está en H.
• Cando H é finito, a proba pódese simplificar: H é un subgrupo se e só se non é baleiro e é pechado baixo produtos. Estas condicións implican que cada elemento a de H xera un subgrupo cíclico finito de H, digamos de orde n, e entón o inverso de a é aⁿ⁻¹.

G é o grupo $\mathbb {Z} /8\mathbb {Z} ,$ que son os enteiros mod 8 mediante adición. O subgrupo H contén só o 0 e o 4, e é isomorfo a $\mathbb {Z} /2\mathbb {Z} .$ Hai catro clases de H á esquerda: H en si, 1 + H, 2 + H e 3 + H (escribindo con notación aditiva xa que este é un grupo aditivo). Entre todos dividen todo o grupo G en conxuntos de igual tamaño e non superpostos. O índice [G : H] é 4.

Cosets e teorema de Lagrange

Dado un subgrupo H e algún a en G, definimos o coset (ou conxunto lateral, ou coclase) esquerdo aH = {ah : h in H}. Como a é invertible, o mapa φ : H → aH dado por φ(h) = ah é unha bixección. Alén diso, cada elemento de G está contido precisamente nun coset esquerdo de H; as clases secundarias da esquerda son as clases de equivalencia correspondentes á relación de equivalencia a₁ ~ a₂ se e só se $a_{1}^{-1}a_{2}$ está en H. O número de clases esquerdas de H chámase índice de H en G e o denotamos por [G : H] .

O teorema de Lagrange afirma que para un grupo finito G e un subgrupo H,

$[G:H]={|G| \over |H|}$

onde |G| e |H| denotan as ordes (ou cardinalidades, número de elementos) de G e H, respectivamente. En particular, a orde de cada subgrupo de G (e a orde de cada elemento de G) debe ser un divisor de |G|.

Os cosets pola deteita defínense de xeito análogo: Ha = {ha : h in H}.

Se aH = Ha para cada a en G, entón dise que H é un subgrupo normal.

Exemplo: subgrupos de Z₈

Sexa G o grupo cíclico Z₈ cuxos elementos son

$G=\left\{0,4,2,6,1,5,3,7\right\}$

e cuxa operación de grupo é a suma módulo 8. A súa táboa de Cayley é

+	0	4	2	6	1	5	3	7
0	0	4	2	6	1	5	3	7
4	4	0	6	2	5	1	7	3
2	2	6	4	0	3	7	5	1
6	6	2	0	4	7	3	1	5
1	1	5	3	7	2	6	4	0
5	5	1	7	3	6	2	0	4
3	3	7	5	1	4	0	6	2
7	7	3	1	5	0	4	2	6

Este grupo ten dous subgrupos non triviais: J = {0, 4} e H = {0, 4, 2, 6} , onde J tamén é un subgrupo de H. O grupo G é cíclico, e tamén o son os seus subgrupos. En xeral, os subgrupos de grupos cíclicos tamén son cíclicos.

Exemplo: Subgrupos de S₄

S₄ é o Grupo simétrico cuxos elementos corresponden ás permutacións de 4 elementos. A continuación móstranse todos os seus subgrupos, ordenados por cardinalidades. Cada grupo (agás os de cardinalidade 1 e 2) está representado pola súa Táboa de Cayley.

24 elementos

Como en todos os grupo, S₄ é un subgrupo de si mesmo (non é subgrupo propio).

Grupo simétrico S4

12 elementos

O grupo alternante A₄ contén só as permutacións pares. É un dos dous subgrupos normais propios non triviais de S₄. (O outro é o seu subgrupo de Klein).

Grupo alternante A₄
Subgrupos:

8 elementos

8 elementos

Grupo diédrico de orde 8
Subgrupos:

Grupo diédrico de orde 8
Subgrupos:

Grupo diédrico de orde 8
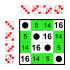
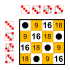
Subgrupos:

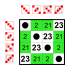
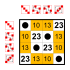
6 elementos

Grupo simétrico S3 Subgrupo:

Grupo simétrico S3 Subgrupo:

Grupo simétrico S3 Subgrupo:

Grupo simétrico S3 Subgrupo:

4 elementos

Grupo de Klein

Grupo de Klein

Grupo de Klein

Grupo de Klein (subgrupo normal)

Grupo cíclico Z4

Grupo cíclico Z4

Grupo cíclico Z4

3 elementos

Grupo cíclico Z3

Grupo cíclico Z3

Grupo cíclico Z3

Grupo cíclico Z3

2 elementos

Cada permutación p de orde 2 xera un subgrupo {1, p }. Estas son as permutacións que só teñen 2 ciclos:

• Hai 6 transposicións cun 2 ciclos. (fondo verde)
• E 3 permutacións con dous ciclos. (fondo branco, números en grosa)

1 elemento

O subgrupo trivial é o único subgrupo de orde 1.

Outros exemplos

• Os enteiros pares forman un subgrupo $2\mathbb {Z}$ do anel dos enteiros $\mathbb {Z} :$ a suma de dous enteiros pares é par e o negativo dun enteiro par é par.
• Un ideal nun anel R é un subgrupo do grupo aditivo de R.
• Un subespazo linear dun espazo vectorial é un subgrupo do grupo aditivo de vectores.
• Nun grupo abeliano, os elementos de orde finita forman un subgrupo chamado subgrupo de torsión.

Véxase tamén

Bibliografía

• Jacobson, Nathan (2009). Basic algebra 1 (2nd ed.). Dover. ISBN 978-0-486-47189-1. .
• Hungerford, Thomas (1974). Algebra (1st ed.). Springer-Verlag. ISBN 9780387905181. .
• Artin, Michael (2011). Algebra (2nd ed.). Prentice Hall. ISBN 9780132413770. .
• Dummit, David S.; Foote, Richard M. (2004). Abstract algebra (3rd ed.). Hoboken, NJ: Wiley. ISBN 9780471452348. OCLC 248917264. 
• Gallian, Joseph A. (2013). Contemporary abstract algebra (8th ed.). Boston, MA: Brooks/Cole Cengage Learning. ISBN 978-1-133-59970-8. OCLC 807255720. 
• Kurzweil, Hans; Stellmacher, Bernd (1998). Theorie der endlichen Gruppen. Springer-Lehrbuch. doi:10.1007/978-3-642-58816-7. 
• Ash, Robert B. (2002). Abstract Algebra: The Basic Graduate Year (en inglés). Department of Mathematics University of Illinois. 

Outros artigos

• Grupo (matemáticas).