Raio de Schwarzschild
O raio de Schwarzschild (tamén chamado historicamente ás veces raio gravitacional) é o un parámetro físico que aparece na solución de Schwarzschild das ecuacións de campo de Einstein, correspondente ao raio que define o horizonte dun burato negro de Schwarzschild. É un raio característico asociado con calquera cantidade de masa. O raio de Schwarzschild recibe ese nome polo astrónomo alemán Karl Schwarzschild, que calculou esta solución exacta para a teoría xeral da relatividade en 1916.
O raio de Schwarzschild vén dado pola expresión
onde G é a constante gravitacional universal, M é a masa do obxecto e c é a velocidade da luz.[1]
Historia[editar | editar a fonte]
En 1916, Karl Schwarzschild obtivo a solución exacta[2][3] ás ecuacións de campo de Einstein para o campo gravitacional fóra dun corpo esfericamente simétrico non rotante (métrica de Schwarzschild). Usando a definición M = Gm/c2, a solución contiña un termo coa forma 1/2M − r; no que o valor de que facía este termo singular acabou por coñecerse como raio de Schwarzschild. A importancia física desta singularidade e se esta singularidade podía darse algunha vez na natureza foi algo debatido durante moitas décadas, e unha aceptación xeral de que a existencia de buratos negros era posible non chegou ata a segunda metade do século XX.
Parámetros[editar | editar a fonte]
O raio de Schwarzschild dun obxecto é proporcional á masa. Segundo isto, o Sol ten un raio de Schwarzschild de aproximadamente 3,0 km, mentres que o da Terra é só duns 9,0 mm. A masa do universo observable ten un raio de Schwarzschild de aproximadamente 13,7 miles de millóns de anos luz.[4][5]
| Obxecto | Masa: | Raio de Schwarzschild: | Densidade de Schwarzschild: |
|---|---|---|---|
| Vía Láctea | 1,6×1042 kg | 2,4×1015 m (~0.25 anos luz) | 0,000029 kg/m3 |
| Burato negro supermasivo en NGC 4889 | 4,2×1040 kg | 6,2×1013 m | 0,042 kg/m3 |
| Burato negro supermasivo na galaxia de Andrómeda | 3,4×1038 kg | 5,0×1011 m | 640 kg/m3 |
| Sagittarius A* (burato negro supermasivo) | 8,2×1036 kg | 1,2×1010 m | 1,1×106 kg/m3 |
| Sol | 1,99×1030 kg | 2,95×103 m | 1,84×1019 kg/m3 |
| Xúpiter | 1,90×1027 kg | 2,82 m | 2,02×1025 kg/m3 |
| Terra | 5,97×1024 kg | 8,87×10-3 m | 2,04×1030 kg/m3 |
| Lúa | 7,35×1022 kg | 1,09×10-4 m | 1,35×1034 kg/m3 |
| Humano | 70 kg | 1,04×10-25 m | 1,49×1076 kg/m3 |
| Big Mac (hamburguesa) | 0,215 kg | 3,19×10-28 m | 1,58×1081 kg/m3 |
| Masa de Planck | 2,18×10-8 kg | 3,23×10-35 m | 1,54×1095 kg/m3 |
Clasificación dos buratos negros polo raio de Schwarzschild[editar | editar a fonte]
Calquera obxecto cuxo radio sexa menor que o seu raio de Schwarzschild denomínase burato negro. A superficie no nivel do raio de Schwarzschild actúa como un horizonte de sucesos nun corpo que non está en rotación (un burato negro en rotación opera de forma lixeiramente diferente). Non poden escapar desta superficie nin a luz nin partículas procedentes da rexión interior, de aí o seu nome de "buratos negros".
Os buratos negros poden clasificarse baseándose no seu radio de Schwarzschild, ou de xeito equivalente, pola súa densidade. Como o raio está linearmente relacionado coa masa, e o volume encerrado corresponde coa terceira potencia do raio, os buratos negros pequenos son, por tanto, moito máis densos que os grandes. O volume encerrado no horizonte de sucesos dos buratos negros máis masivos ten unha densidade inferior ao das estrelas da secuencia principal.
Burato negro supermasivo[editar | editar a fonte]
Un burato negro supermasivo é o tipo máis grande de burato negro, aínda que hai poucos criterios oficiais sobre como ten que ser exactamnte un obxecto para ser considerado así, pero crese que debe ter centos ou miles ou ata miles de millóns de masas solares. (Detectáronse buratos negros supermasivos de ata 21 mil millóns de masas solares (2,1 × 1010 M☉), como NGC 4889.)[6] A diferenza dos buratos negros estelares, os supermasivos teñen densidades comparativaemnte menores. (Nótese que un burato negro é unha rexión esférica do espazo que rodea a singularidade que está no seu centro, pero el non é unha singularidade.) Tendo iso presente, a densidade media dos buratos negros supermasivos pode ser menor que a densidade da auga.
O raio de Schwarzschild dun corpo é proporcional á súa masa e, por tanto, ao seu volume, asumindo que o corpo ten unha masa-densidade constante.[7] En contraste, o raio físico do corpo é proporcional á raíz cúbica do seu volume. Por tanto, a medida que o corpo acumula materia a unha densidade dada fixa (por exemplo, 103 kg/m3, a densidade da auga), o seu raio de Schwarzschild incrementarase máis rapidamente que o seu raio físico. Cando un corpo desta densidade creceu ata unhas 136 millóns de masas solares (1,36 × 108 M☉), o seu raio físico sería superado polo seu raio de Schwarzschild, e así formaría un burato negro supermasivo.
Crese que os buratos negros supermasivos como este non se forman inmediatamente a partir do colapso singular dun cúmulo de estrelas, senón que poden comezar a súa existencia como buratos negros de tamaño estelar e crecer facéndose máis grandes por acreción sucesiva de materia ou incluso doutros buratos negros.[8]
O raio de Schwarzschild do burato negro supermasivo do noso centro galáctico sería de aproximadamente 13,3 millóns de quilómetros.[9]
Burato negro estelar[editar | editar a fonte]
Os buratos negros estelares teñen densidades moito maiores que os supermasivos. Se se acumula materia a densidade nuclear (a densidade que hai no núcleo dun átomo, que é duns 1018 kg/m3; densidade que tamén se alcanza nunha estrela e neutróns), esta acumulación estará dentro do seu propio raio de Schwarzschild cunhas 3 masas solares e sería un burato negro estelar.
Burato negro primordial[editar | editar a fonte]
Unha masa pequena ten un raio de Schwarzschild extremadamente pequeno. Unha masa similar á do Monte Everest[10][nota 1] ten un raio de Schwarzschild moito menor que 1 nanómetro.[nota 2] A súa densidade media con ese tamaño sería tan alta que non se coñece ningún mecanismo que puidese formar un obxecto tan extremadamente compacto. Ditos buratos negros probablemente puideron formarse nun estadio temperán da evolución do Universo, xusto despois do Big Bang, cando as densidades eran extremadamente altas. Por tanto, estes buratos negros en miniatura hipotéticos chámanse buratos negros primordiais.
Outros usos[editar | editar a fonte]
Na dilatación do tempo gravitacional[editar | editar a fonte]
A dilatación do tempo gravitacional preto dun corpo case esférico en lenta rotación, como a Terra e o Sol pode aproximarse razoablemente usando o raio de Schwarzschild da seguinte maneira:
onde:
- tr é o tempo pasado para un observador na coordenada radial r dentro do campo gravitatorio;
- t é o tempo pasado para un observador que está lonxe do obxecto masivo (e, por tanto, fóra do seu campo gravitatorio);
- r é a coordenada radial do observador (que é análoga da distancia clásica desde o centro do obxecto);
- rs é o raio de Schwarzschild.
Os resultados do experimento de Pound–Rebka de 1959 son consistentes coas predicións feitas pola relatividade xeral. Medindo a dilatación do tempo gravitacional da Terra, este experimento mediu indirectamente o raio de Schwarzschild da Terra.
En campos gravitatorios newtonianos[editar | editar a fonte]
O campo gravitatorio newtoniano preto dun corpo esférico grande en lenta rotación pode aproximarse razoablemente usando o raio de Schwarzschild da seguinte maneira:
e
Por tanto, dividindo a expresión de arriba pola de abaixo:
onde:
- g é a aceleración gravitatoria na coordenada radial r;
- rs é o raio de Schwarzschild do corpo central gravitante;
- r é a coordenada radial;
- c é a velocidade da luz no baleiro.
Na superficie da Terra:
En órbitas keplerianas[editar | editar a fonte]
Para todas as órbitas circulares arredor dun corpo central dado:
Por tanto,
pero
- (derivada)
Por tanto,
onde:
- r é o raio da órbita;
- rs é o raio de Schwarzschild do corpo central gravitante;
- v é a velocidade orbital;
- c é a velocidade da luz no baleiro.
Esta igualdade pode ser xeneralizada a órbitas elípticas así:
onde:
- a é o semieixe maior;
- T é o período orbital.
Para a Terra orbitando o Sol sería:
Órbitas circulares relativistas e a esfera de fotóns[editar | editar a fonte]
A ecuación kepleriana para as órbitas circulares pode xeneralizarse para a ecuación relativista para as órbitas circulares representando unha dilatación do tempo no termo velocidade:
Esta ecuación final indica que un obxecto que orbita á velocidade da luz tería un raio orbital de 1,5 veces o raio de Schwarzschild. Esta é unha órbita especial chamada esfera de fotóns.
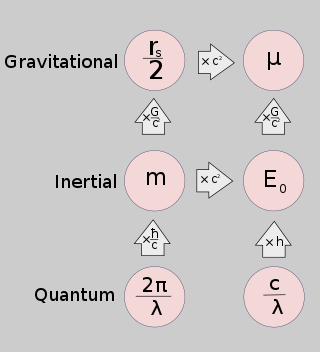
Raio de Schwarzschild para a masa de Planck[editar | editar a fonte]
Para a masa de Planck , o raio de Schwarzschild e a lonxitude de onda de Compton son da mesma orde que a lonxitude de Planck .
Notas[editar | editar a fonte]
- Notas a rodapé
- Referencias
- ↑ Kutner, Marc (2003). Astronomy: A Physical Perspective. Cambridge University Press. p. 148.
- ↑ K. Schwarzschild, "Über das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie", Sitzungsberichte der Deutschen Akademie der Wissenschaften zu Berlin, Klasse fur Mathematik, Physik, und Technik (1916) pp 189.
- ↑ K. Schwarzschild, "Über das Gravitationsfeld einer Kugel aus inkompressibler Flussigkeit nach der Einsteinschen Theorie", Sitzungsberichte der Deutschen Akademie der Wissenschaften zu Berlin, Klasse fur Mathematik, Physik, und Technik (1916) pp 424.
- ↑ Valev, Dimitar (outubro de 2008). "Consequences from conservation of the total density of the universe during the expansion". arXiv:1008.0933 [physics.gen-ph].
- ↑ Deza, Michel Marie; Deza, Elena (Oct 28, 2012). Encyclopedia of Distances (2nd ed.). Heidelberg: Springer Science & Business Media. p. 452. ISBN 978-3-642-30958-8. doi:10.1007/978-3-642-30958-8. Consultado o 8 de decembro de 2014.
- ↑ McConnell, Nicholas J. (2011-12-08). "Two ten-billion-solar-mass black holes at the centres of giant elliptical galaxies" (PDF). Nature 480: 215–218. doi:10.1038/nature10636. Arquivado dende o orixinal (PDF) o 01 de setembro de 2014. Consultado o 2011-12-06.
- ↑ Robert H. Sanders (2013). Revealing the Heart of the Galaxy: The Milky Way and its Black Hole. Cambridge University Press. p. 36. ISBN 978-1-107-51274-0.
- ↑ Paolo Coppi, Department of Astronomy, Yale University Massive Black Hole Growth and Formation
- ↑ http://www.thetimes.co.uk/tto/news/world/article1967154.ece
- ↑ 10,0 10,1 "How does the mass of one mole of M&M’s compare to the mass of Mount Everest?" (PDF). School of Science and Technology, Singapore. marzo de 2003. Arquivado dende o orixinal (PDF) o 10 de decembro de 2014. Consultado o 8 de decembro de 2014.
Se se asume que o Monte Everest é un cono dunha altura de 8 850 m e un raio de 5 000 m, entón o seu volume pode calcularse usando a seguinte ecuación: volume = πr2h/3 [...] O Monte Everest está composto de granito, que ten unha densidade de 2750 kg/m3.
Véxase tamén[editar | editar a fonte]
Outros artigos[editar | editar a fonte]
- Burato negro
- límite de Chandrasekhar, un segundo requisito para a formación de buratos negros
Clasificación dos buratos negros por tipo:
- Burato negro estático ou rotante
- Burato negro rotante ou de Kerr
- Burato negro cargado ou de Newman ou de Kerr-Newman
Clasificación dos buratos negros por masa:
- Microburato negro e extradimensional
- Burato negro primordial
- Burato negro estelar, pode ser estático ou rotante
- Burato negro supermasivo, pode ser estático ou rotante























