Relación binaria
| Relacións binarias transitivas | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Todas as definicións requiren tacitamente que a relación homoxénea sexa transitiva: para todo se e entón |
Unha relación binaria R é o subconxunto dos elementos do produto cartesiano que cumpren a condición:
Clasificación das relacións binarias
[editar | editar a fonte]
No esquema pódese ver algunhas estruturas alxébricas ou subtipos de relación binaria. Empregaremos este esquema para ver estes casos.
En primeiro lugar diferenciamos as relacións binarias homoxéneas, das heteroxéneas. Nas primeiras, a relación binaria establécese entre os elementos dun único conxunto, mentres que nas segundas establécense relacións entre dous conxuntos distintos. Unha relación homoxénea pode ser tratada como heteroxénea cos mesmos subtipos, mais non ao contrario.
Relación homoxénea
[editar | editar a fonte]Unha relación binaria R é homoxénea se os dous conxuntos implicados son o mesmo:
Dado que e son o mesmo conxunto, pode representarse como:
- ou tamén como
Relación heteroxénea
[editar | editar a fonte]Unha relación binaria R é heteroxénea se os dous conxuntos implicados non son iguais:
Conceptos previos
[editar | editar a fonte]Par ordenado
[editar | editar a fonte]Se temos os conxuntos e descríbese o par ordenado que cumpre e .
Represéntase como:
Produto cartesiano
[editar | editar a fonte]Definidos os conxuntos:
O produto cartesiano descríbese na táboa anterior.
A relación binaria fica definida como
Operacións con relacións binarias
[editar | editar a fonte]Unión
[editar | editar a fonte]Se R e S son relacións binarias sobre os conxuntos X e Y, entón é a relación de unión de R e S sobre X e Y.
Por exemplo, é a unión de < e =.
Intersección
[editar | editar a fonte]Se R e S son relacións binarias sobre os conxuntos X e Y entón é a relación de intersección de R e S sobre X e Y.
Por exemplo, a relación "é divisible por 6" é a intersección das relacións "é divisible por 3" e "é divisible por 2".
Composición
[editar | editar a fonte]Se R é unha relación binaria sobre os conxuntos X e Y, e S é unha relación binaria sobre os conxuntos Y e Z entón (tamén denotado como R; S) é a relación de composición de R e S sobre X e Z.
A orde de R e S na notación usada aquí concorda coa orde de notación estándar para composición de funcións. Por exemplo, a composición (é o pai de)(é a nai de) produce (é o avó materno de).
Inversa
[editar | editar a fonte]Se R é unha relación binaria sobre os conxuntos X e Y, entón é a relación inversa,[1] [2] de R sobre Y e X. Tamén se pode representar como .
Por exemplo, é a inversa de si mesmo, e e son o inverso do outro.
Complementario
[editar | editar a fonte]Se R é unha relación binaria sobre os conxuntos X e Y entón (tamén denotada por R ou ¬ R) é a relación complementaria de R sobre X e Y.
Por exemplo, e son complementarios mutuos.
O complemento da relación inversa é a inversa do complemento:
Restrición
[editar | editar a fonte]Se R é unha relación homoxénea binaria sobre un conxunto X e S é un subconxunto de X entón é a relación de restrición de R a S sobre X.
Relación binaria homoxénea
[editar | editar a fonte]Unha relación binaria estabelécese entre os elementos dun único conxunto.
Exemplo
[editar | editar a fonte]Se temos un único conxunto , podemos definir unha relación binaria R como un conxunto de pares ordenados:
- ou ,
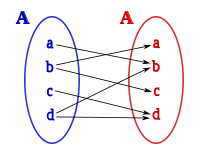
Se o elemento inicial está relacionado co elemento final, non implica necesariamente que haxa unha relación desde o elemento final ata o elemento inicial. Por iso é importante que sexan pares ordenados.
Imos representar agora esa mesma relación binaria como un subconxunto do produto cartesiano:
| d | (a, d) | (b, d) | (c, d) | (d, d) |
| c | (a, c) | (b, c) | (c, c) | (d, c) |
| b | (a, b) | (b, b) | (c, b) | (d, b) |
| a | (a, a) | (b, a) | (c, a) | (d, a) |
| A×A | a | b | c | d |
O subconxunto R da relación binaria son os pares en letra grosa e o podemos representar tamén como:
Propiedades da relación binaria homoxénea
[editar | editar a fonte]Propiedade reflexiva
[editar | editar a fonte]- Artigo principal: Relación reflexiva.
Dicimos que unha relación ten a propiedade reflexiva, se todo elemento está relacionado consigo mesmo.
Isto é, para todo elemento e pertencente ao conxunto A, o par ordenado (e,e) pertence á relación binaria R.
Propiedade antirreflexiva
[editar | editar a fonte]Unha relación binaria ten a propiedade antirreflexiva, ou irreflexiva, se ningún elemento do conxunto está relacionado consigo mesmo:
isto é, non existe ningún elemento a no conxunto A que cumpra que: (a,a) pertence a R.
Propiedade simétrica
[editar | editar a fonte]- Artigo principal: Relación simétrica.
Dicimos que unha relación binaria ten a propiedade simétrica cando se se cumpre que un par ordenado (a,b) pertence á relación entón o par (b,a) tamén pertence a esa relación:
Propiedade antisimétrica
[editar | editar a fonte]Dise que unha relación binaria ten a propiedade antisimétrica se os pares ordenados (a,b) e (b,a) pertencen á relación, entón a = b:
Isto é, non hai ningún par de elementos distintos relacionados entre si en ambos os sentidos.
Propiedade transitiva
[editar | editar a fonte]- Artigo principal: Relación transitiva.
Unha relación binaria ten a propiedade transitiva cando, dados os elementos a, b, c do conxunto, se a está relacionado con b e b está relacionado con c, entón a está relacionado con c:
Propiedade intransitiva
[editar | editar a fonte]Unha relación binaria ten a propiedade intransitiva cando, dados os elementos a, b, c do conxunto, se a está relacionado con b e b está relacionado con c, entón a non está relacionado con c:
Propiedade total
[editar | editar a fonte]- Artigo principal: Relación conexa.
Dicimos que unha relación binaria é total: se para todo elemento do conxunto: a, b; ou a está relacionado con b ou b está relacionado con a, isto é, o grafo da relación é conexo:
Relacións homoxéneas particulares
[editar | editar a fonte]Algunhas relacións homoxéneas particulares sobre un conxunto X (con elementos arbitrarios x1, x2) son:
- Relación baleira
- E = ∅;
isto é, x1E x2 non acontece nunca;
- E = ∅;
- Relación universal
- U = X × X;
isto é, x1U x2 sempre acontece (están relacionados todos con todos);
- U = X × X;
- Relación identidade (ver tamén Función identidade)
- I = {(x, x) | x ∈ X};
isto é, x1I x2 cúmprese se e só se x1 = x2.
- I = {(x, x) | x ∈ X};
Clases das relacións binarias homoxéneas
[editar | editar a fonte]Relación reflexiva
[editar | editar a fonte]As relacións reflexivas son as definidas do seguinte modo:
|
O caso máis claro de propiedade reflexiva é o de igualdade matemática.
Vemos un exemplo:

Temos un conxunto A, formado polos seguintes elementos:
E temos unha relación R entre os elementos do conxunto, definida así:
Pódese ver que os pares ordenados que teñen os seus dous termos iguais pertencen á relación definida:
Daquela a relación R é reflexiva.
Relación non reflexiva
[editar | editar a fonte]Se non todos os elementos están relacionados consigo mesmos a relación é non reflexiva.
Temos dous tipos:
- Se algún elemento, mais non todos, é reflexivo a relación é arreflexiva
- Se ningún elemento é reflexivo a relación é antirreflexiva (ou irreflexiva)
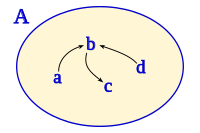
Podemos ver que:
Relación de dependencia
[editar | editar a fonte]Unha relación binaria é unha relación de dependencia se é reflexiva e simétrica:
|
Por exemplo se temos o conxunto dos números naturais, e definimos a distáncia D entre dous números, como o valor absoluto da súa diferenza.
- ,
e dicimos que dous números están próximos se
Daquela para a relación de proximidade dentro dos números naturais é unha relación de dependencia, posto que:
1. Cúmprese a propiedade reflexiva posto que:
2. Cúmprese a propiedade simétrica:
3. Non se cumpre a propiedade transitiva, dado que:
que a distancia entre a e b sexa como máximo D e que a distancia entre b e c non supere D, non implica necesariamente que a distancia entre a e c non sexa maior que D.
Esta relación de dependencia entre os números pola súa distancia non é unha clase de equivalencia, como se verá máis adiante.
Conxunto preordenado
[editar | editar a fonte]- Artigo principal: Preorde.
Unha relación binaria define un conxunto preordenado se é reflexiva e transitiva.
|
Relación de equivalencia
[editar | editar a fonte]- Artigo principal: Relación de equivalencia.
Unha relación binaria é unha relación de equivalencia se é reflexiva, simétrica e transitiva:[3]
|
Unha relación de equivalencia define dentro do conxunto A o que se denominan, clases de equivalencia, unha clase de equivalencia é cada un dos subconxuntos nos que a relación de equivalencia divide ao conxunto A, entre eles son disxuntos, e a unión de todos eles é o conxunto A, vexamos un exemplo.
A congruencia módulo n dos números naturais (residuo da división enteira entre n), vemos que é unha relación de equivalencia. Por exemplo,
,
,
.
Formalizamos as condicións:
é reflexiva:
é simétrica:
é transitiva
Conxunto parcialmente ordenado
[editar | editar a fonte]- Artigo principal: Conxunto parcialmente ordenado.
Un conxunto A dise que está parcialmente ordenado respecto a unha relación binaria R se a relación R é reflexiva, transitiva e antisimétrica:
|
Tomando un conxunto A, formado, por exemplo, polos elementos:
E o seu conxunto de partes
Imos chamar a cada un destes subconxuntos:
E tomando dous destes subconxuntos dicimos que están relacionados por pertenza se o primeiro é subconxunto do segundo:
A relación pertenza entre os conxuntos de partes de A, é un conxunto parcialmente ordenado, ao ser:
Reflexiva
Transitiva:
Antisimetrica:
Por tanto o conxunto de partes de A, respecto da relación binaria pertenza é un conxunto parcialmente ordenado.
Esta relación non é total dado que:
Que se denominan elementos ou pares non comparables. Os pares de conxuntos non comparables son:

Vendo o diagrama, os conxuntos que se poden alcanzar seguindo o sentido das frechas denomínanse comparables e determinan a estrutura da orde parcial.
Conxunto limitado
[editar | editar a fonte]Un conxunto de números reais está limitado se e só se ten un límite superior e outro inferior. Esta definición é extensible a subconxuntos de calquera conxunto parcialmente ordenado. Hai que ter en conta que este concepto máis xeral de dimensionamento non se corresponde cunha noción de tamaño. Hai distintos tipos de límites e os seus elementos relacionados en función do tipo de orde, parcial ou total:
- Elemento maior e menor
- Ínfimo e supremo
- Elemento maiorante e minorante
- Límite superior e límite inferior
Conxunto con orde total e limitado
[editar | editar a fonte]- Artigo principal: Orde total.
Se temos un conxunto A e unha relación binaria definida entre os elementos de A, que expresaremos e a relación represéntase:
Dicimos que se definiu unha orde total no conxunto A, se a relación cumpre as propiedades:
- 1. Reflexiva.
- 2. Antisimétrica.
- 3. Transitiva.
- 4. É, ademais, unha relación total, é dicir, cúmprese que todos os elementos dun conxunto con orde total son comparables:
Dado un conxunto A no que se definiu unha relación binaria , sendo un conxunto totalmente ordenado, o elemento y de A que cumpre:
Denomínase máximo e define un límite superior en A; o elemento máximo é único. Se o conxunto A e a relación binaria é unha orde total e ten máximo, entón é un conxunto con orde total e limitado superiormente.
Do mesmo xeito o elemento z de A que cumpre:
Denomínase mínimo e define un límite inferior en A; o elemento mínimo é único. Se o conxunto A e a relación binaria é unha orde total e ten mínimo, entón é un conxunto con orde total e limitada inferiormente.
Un conxunto con orde total dicimos simplemente que é limitado, se está limitado superior e inferiormente.
Relación heteroxénea
[editar | editar a fonte]Unha relación binaria entre dous conxuntos A e B, denomínase heteroxénea cando A é distinto de B:
- O conxunto A é o conxunto inicial (dominio).
- O conxunto B é o conxunto final (codominio).
- O subconxunto de A dos elementos a que forman parte dalgunha relación R (a,b) é o conxunto orixe.
- O subconxunto de B dos elementos b que forman parte dalgunha relación R (a,b) é o conxunto imaxe.
Conceptos previos
[editar | editar a fonte]- A condición de existencia de imaxe garantiza que tomando un elemento calquera a de A ten polo menos unha imaxe b en B.
- A condición de existencia de orixe garantiza que todo elemento b de B ten polo menos unha orixe a en A.
- A condición de unicidade de imaxe garantiza que os elementos a de A que están relacionados con algún b de B están relacionados con un único elemento b de B, é dicir:
- A condición de unicidade de orixe di que os elementos b de B que están relacionados con algún a de A están relacionados só con un único elemento a de A, é dicir:
Tipos de relacións binarias heteroxéneas
[editar | editar a fonte]Partindo das características das relacións binarias heteroxéneas, podemos diferenciar os seguintes casos.
Correspondencia unívoca
[editar | editar a fonte]Unha correspondencia é unívoca se cumpre a condición de unicidade de imaxe:
|
Esta condición é necesaria e suficiente para que unha correspondencia sexa considerada unívoca.
Correspondencia biunívoca
[editar | editar a fonte]Unha correspondencia é biunívoca se cumpre as condicións de unicidade de imaxe e unicidade de orixe:
|
Aplicación
[editar | editar a fonte]Unha correspondencia denomínase aplicación se todo elemento de A admite unha única imaxe en B., [4] [5] [6] isto é se cumpre a condición de unicidade de imaxe e de existencia de imaxe.
Unha aplicación f de A en B, sendo A e B dous conxuntos calquera, é unha correspondencia entre A e B, total e unívoca.[7]
Se a aplicación representámola como R, teremos:
pola que definimos unha aplicación que a cada elemento a de A asígnaselle un único b de B.
Para todo a de A, cúmprese que existe un único b de B, tal que b é o resultado R(a).
|
Se unha correspondencia cumpre estas dúas condicións denomínase aplicación.
Aplicación inxectiva
[editar | editar a fonte]- Artigo principal: inxectiva.
Unha correspondencia é unha aplicación inxectiva se cumpre a condición de unicidade de imaxe, existencia de imaxe e unicidade de orixe.
|
Aplicación sobrexectiva
[editar | editar a fonte]- Artigo principal: sobrexectiva.
Unha correspondencia chámase Aplicación sobrexectiva se cumpre a condición de unicidade de imaxe, existencia de imaxe e existencia de orixe:
|
Aplicación bixectiva
[editar | editar a fonte]- Artigo principal: bixectiva.
Unha correspondencia é unha aplicación bixectiva se cumpre as condicións de unicidade de imaxe, existencia de imaxe, unicidade de orixe e existencia de orixe:
|
Unha Aplicación é bixectiva, se é inxectiva e sobrexectiva.
Outros tipos de relación
[editar | editar a fonte]Se se permiten relacións sobre clases propias:
- Tipo Conxunto (tamén chamado local): para todas as , a clase de tódalas tal que , é dicir, , é un conxunto. Por exemplo, a relación é de tipo conxunto, e todas as relacións de dous conxuntos son de tipo conxunto.[8]
Notas
[editar | editar a fonte]- ↑ Garrett Birkhoff & Thomas Bartee (1970) Álxebra aplicada moderna, páxina 35, McGraw-Hill
- ↑ Mary P. Dolciani (1962) Modern Algebra: Structure and Method, Libro 2, páxina 339, Houghton Mifflin
- ↑ Gutiérrez Gómez, Andrés; García Castro, Fernando (1981). "2.3. Relaciones de equivalencia". Álgebra lineal (1 ed.). Ediciones Pirámide, S.A. p. 74. ISBN 978-84-368-0174-3.
- ↑ José Juan Carreño Carreño (2008). "ÁLXEBRA Curso 2008/09" (pdf). p. 13.[Ligazón morta]
- ↑ Mario López Gómez (2005). "Algebra I" (pdf). p. 5 />.[Ligazón morta]Gregori Gregori, Valentín; Ferrando, J. C. (2011). Matemática discreta (8 ed.). Editorial Reverté, S.A. p. 48. ISBN 978-84-291-5179-4.
- ↑ Ayres, Frank (1992). Álxebra moderna (1 ed.). McGraw-Hill. p. 6. ISBN 968-422-917-8.
- ↑ Gran enciclopedia temática Praza. Matemáticas (2 ed.). Praza & Janés Editores, S.A. 1993. p. 400. ISBN 978-84-01-61659-4. segundo outra nomenclatura.
- ↑ Kunen, Kenneth (1980). Set theory: an introduction to independence proofs. North-Holland. p. 102. ISBN 0-444-85401-0. Zbl 0443.03021.
Véxase tamén
[editar | editar a fonte]| Wikimedia Commons ten máis contidos multimedia na categoría: Relación binaria |
Bibliografía
[editar | editar a fonte]- González Gómez, Antonia (2009). Álgebra lineal. Fundación Conde del Valle de Salazar. ISBN 978-84-96442-28-3.
- Baquerizo Azofra, Clara (2008). Matemática discreta y álgebra lineal (1 ed.). Martín Gómez, Emilia. ISBN 978-84-612-3787-6.
- Hortalá González, María Teresa (2001). Matemática discreta y lógica matemática (2 ed.). Editorial Complutense, S.A. ISBN 978-84-7491-650-8.
- Climent Coloma, Joan Josep (2001). Álgebra. Teoría de conjuntos y estructuras algebraicas (1 ed.). Editorial Club Universitario. ISBN 978-84-8454-081-6.
- Gutiérrez Gómez, Andrés; García Castro, Fernando (1981). Álgebra lineal (1 ed.). Ediciones Pirámide, S.A. ISBN 978-84-368-0174-3.
- Losada Rodríguez, Ramón (1978). Análisis matemático. Ediciones Pirámide, S.A. ISBN 978-84-368-0096-8.
- Losada Rodríguez, Ramón (1973). Conjuntos Álgebra Lineal (2 ed.). ISBN 978-84-400-6592-6.





























































































































