Asíntota

Gráfica de dúas hipérboles e as súas asíntotas no plano cartesiano.

Tratado sobre cónicas, s. XVIII

En matemáticas, chámase asíntota da gráfica dunha función, a unha recta á que se aproxima continuamente a gráfica desa función, é dicir, que a distancia entre as dúas tende a cero a a medida que se estenden indefinidamente.

Historia

A palabra asíntota deriva do grego: ἀσύμπτωτος asýmptōtos, «aquilo que non cae»; onde a- posúe un valor privativo (= non), mentres que sym-ptōtos indica aquilo que «cae» ou «cae xunto (a algo)». Adoita darse a definición de asíntota como curvas que «non se encontran nunca». Esta interpretación intuitiva foi plasmada por Apolonio de Perga no seu coñecido tratado Sobre as seccións cónicas, para referirse a unha recta que non interseca unha rama dunha hipérbole.

En xeometría, o comportamento asintótico refírese a unha eventual propiedade entre curvas, e máis precisamente, entre funcións ou partes de funcións: segmentos de recta, ramas de hipérbole ou de parábola etc. É neste sentido en que se fala de «recta asintótica» como tanxente ao infinito dunha rama parabólica, ou ben de curvas asintóticas.

O seu estudo máis profundo desborda o campo de aplicación da xeometría elemental e o trazado de curvas planas; co desenvolvemento da álxebra e do cálculo infinitesimal, as nocións intuitivas «tende a infinito» e «tende a cero» formalízanse co concepto de límite matemático, e con iso tamén o cálculo de asíntotas.

Gráfica de asíntotas

Véxase tamén: Gráfica dunha función.

As asíntotas axudan á representación de curvas, proporcionan un soporte estrutural e indican o seu comportamento a longo prazo. En tanto que liñas rectas, a ecuación dunha asíntota é simplemente a dunha recta, e a súa expresión analítica dependerá da elección do sistema de referencia (y = m•x + b en coordenadas cartesianas).

Se ben adoitan representarse nun mesmo sistema de coordenadas, as asíntotas non forman parte da expresión analítica da función, polo que -en numerosos exemplos- non están incluídas explicitamente dentro da gráfica, ou ben indícanse cunha liña punteada.

En moitos casos, as asíntotas coinciden cos eixes de coordenadas, é dicir que as súas ecuacións en coordenadas cartesianas serán: x = 0, y = 0.

Distínguense tres tipos:

• Asíntotas verticais: rectas perpendiculares ao eixe das abscisas, de ecuación x = constante.
• Asíntotas horizontais: rectas perpendiculares ao eixe das ordenadas, de ecuación y = constante.
• Asíntotas oblicuas: se non son paralelas ou perpendiculares aos eixes, de ecuación y = m•x + b.

As ramas da función teñen asíntotas.

Os eixes son as asíntotas.

As ramas da función teñen asíntotas.

Comportamento asintótico entre unha curva e unha recta.

Determinación analítica de asíntotas

En análise, cálculo e xeometría analítica, o comportamento de funcións non triviais nas proximidades de puntos de «indefinición» (tales como a división por cero ou as formas indeterminadas) proporciona información valiosa sobre a súa gráfica, e neste contexto as asíntotas xorden naturalmente como «solucións» (ou direccións) nestes puntos. Neste sentido, unha función pode ter unha «asíntota pola dereita» pero non pola esquerda (ou viceversa); ou ben unha recta pode intersecar unha curva nun número finito (ou infinito) de puntos, e presentar aínda así un comportamento asintótico.

Cálculo de asíntotas por medio de límites

Véxase tamén: Límite matemático.

Asíntota vertical

Chámase asíntota vertical dunha rama dunha curva y = f(x), á recta paralela ao eixe e que fai que a rama desa función tenda a infinito. Se existe algún destes dous límites:

$\lim _{x\to a^{-}}f(x)=\pm \infty$

$\lim _{x\to a^{+}}f(x)=\pm \infty$

a recta x = a denomínase asíntota vertical.

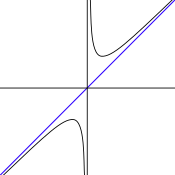
Exemplos: logaritmo neperiano, tanxente

Asíntota horizontal

Chámase asíntota horizontal dunha rama dunha curva y = f(x) á recta paralela ao eixe x que fai que a rama desa función tenda a infinito. Se existe o límite:

$\lim _{x\to \pm \infty }f(x)=a$, sendo a un valor finito

a recta y = a é unha asíntota horizontal.

Exemplos: función exponencial, tanxente hiperbólica

Asíntota oblicua

A recta de ecuación y = mx + b (m ≠ 0) será unha asíntota oblicua se: $\lim _{x\to \pm \infty }[f(x)-(mx+b)]=0$.

Os valores de m e de b calcúlanse coas fórmulas: $m=\lim _{x\to \pm \infty }{f(x) \over x}$; $b=\lim _{x\to \pm \infty }{f(x)-mx}$.

Asíntotas de funcións racionais

Véxase tamén: Función racional.

Na representación gráfica dunha función racional ten un papel esencial, cando existen, as asíntotas. Se ben é posible aplicar o método por límites descrito anteriormente, no caso de funcións racionais, adoitan empregarse técnicas algorítmicas que non precisan da análise matemática.

Unha función racional pode ter máis dunha asíntota vertical, pero só unha que sexa horizontal ou oblicua (é dicir que se ten asíntota horizontal entón non pode ter asíntota oblicua, e viceversa).

• O dominio da función determina as asíntotas verticais.
• A división de polinomios proporciona as asíntotas horizontais u oblicuas.

Para maior claridade, sexa:

${\frac {A(x)}{B(x)}}={\frac {a_{m}x^{m}+a_{m-1}x^{m-1}+...+a_{1}x+a_{0}}{b_{n}x^{n}+b_{n-1}x^{n-1}+...+b_{1}x+b_{0}}}$

• Se $m<n\,$, hai unha asíntota horizontal de ecuación: y = 0.
• Se $m=n\,$, hai unha asíntota horizontal de ecuación: y = a_m/b_n (ou cociente dos coeficientes principais).
• Se $m>n\,$, non hai asíntota horizontal; se o grao do numerador é exactamente un máis có do denominador, hai unha asíntota oblicua, e a súa ecuación vén dada polo cociente da división dos polinomios.

As asíntotas verticais danse nos valores que anulan o denominador pero non o numerador. Se hai unha raíz común, compárase a multiplicidade das raíces.

Exemplos

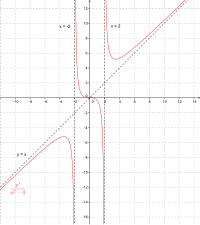
1. A función homográfica $f(x)={\frac {ax+b}{cx+d}}$ ten dúas asíntotas, AV: x = -d/c, AH: y = a/c
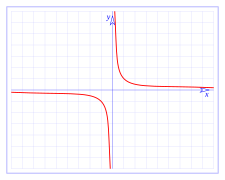
2. No caso particular $y={\frac {1}{x}}$ as asíntotas son os propios eixes cartesianos.

Función racional con asíntota oblicua e dúas asíntotas verticais

$y={\frac {1}{x}}$

Función racional con asíntota horizontal e dúas asíntotas verticais

Asíntotas de curvas polares

As asíntotas a unha curva descrita por unha ecuación en coordenadas polares $r=\rho (\theta )\$, son as curvas que se obteñen cando r ou θ tenden a infinito ou cara a un valor dado.

Recta asintótica

Unha curva polar terá unha dirección asintótica cando, para $\theta _{0}\$ dado,

$\lim _{\theta \to \theta _{0}}\rho (\theta )=\infty$.

A curva ten entón unha recta asintótica se existe un real λ tal que

$\lim _{\theta \to \theta _{0}}\rho (\theta )sin(\theta -\theta _{0})=\lambda$

e achégase á recta de ecuación

$\rho (\theta )={\frac {\lambda }{sin(\theta -\theta _{0})}}$.

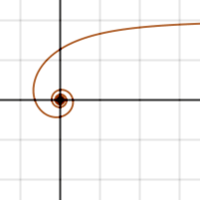
Círculo asintótico

Unha curva polar terá un círculo asintótico se existe un $\rho _{0}\$ dado, tal que

$\lim _{\theta \to \infty }\rho (\theta )=\rho _{0}$.

A curva enrólase sobre o círculo de ecuación $\rho =\rho _{0}\$ se na veciñanza de θ $\rho (\theta )\ <\rho _{0}\$ entón a curva enrólase ao interior do círculo asintótico; inversamente, se $\rho (\theta )>\rho _{0}\$, entón enrólase ao exterior.

Exemplos

As máis variadas funcións posúen comportamento asintótico: dende a simple gráfica dunha curva plana en dúas dimensións, ata superficies tridimensionais máis complexas; tanto en funcións alxébricas (polinómicas, racionais) como transcendentes (trigonométricas, logarítmicas, exponenciais), xa sexa en coordenadas cartesianas, polares etc.

As asíntotas actúan como curvas guía para graficar outras curvas, ou funcións.

Funcións transcendentes

tan(x)
Asíntotas verticais cada π.

ln(x)
Asíntota vertical cara a abaixo.

exp(x)
Asíntota horizontal pola esquerda.

Curvas polares

Espiral inversa de Arquímedes

$r\theta =a\$

Asíntota en $y=a\$.

Curva de Kappa

Folium de Descartes
$r(\theta )={\frac {3a\sin \theta \cos \theta }{\sin ^{3}\theta +\cos ^{3}\theta }}$

Asíntota en $x+y+a=0\$.

Curvas asintóticas

Tridente de Newton:
$xy=ax^{3}+bx^{2}+cx+d\,$.

Asíntotas: a parábola de ecuación $\,y=ax^{2}+bx+c$,
e a hipérbole de ecuación $y={\frac {d}{x}}$.

Función: $y={\frac {x^{3}+2x^{2}+3x+4}{x}}$,

Asíntota curvilínea: $y=x^{2}+2x+3\$.

Superficies e estruturas

Trompeta de Torricelli
A superficie é asintótica a unha recta que pase polo seu centro.

Neste exemplo, obtida ao rotar a curva y=1/x sobre o eixe x.

Hiperboloide

Asíntotas
A estreita relación entre asíntotas e hipérboles prolóngase, en tres dimensións, aos hiperboloides, aproximándose a un cono asintótico.

En tanto que soportes rectos, as liñas asintóticas proporcionan estabilidade, como se aprecia nas estruturas hiperboloides.

Véxase tamén

Bibliografía

• Casteleiro Villalba, José Manuel (2006). Introducción al análisis matemático I (en castelán). ESIC. 
• Alamar Penadés, Miguel (2005). Matemáticas básicas (en castelán). Univ. Politéc. Valencia. 
• Pinzón Escamilla, Álvaro (1977). Cálculo I: diferencial (en castelán). Universidad Nac. del Litoral. 
• Prado Perez, Carlos Daniel (2006). Precálculo (en castelán). Pearson Educación. 
• Pérez Carreras, Pedro (1989). Cálculo infinitesimal (en castelán). Universidad Politécnica de Valencia. 
• Engler; Müller; Vrancken; Hecklein (2000). Funciones (en castelán). Universidad Nacional del Litoral. 
• Frost, P. (1918). An elementary treatise on curve tracing (en inglés). 

Outros artigos

• Sección cónica
• Infinito
• División por cero
• Derivada
• Clasificación de descontinuidades
• Análise de algoritmos
• Análise asintótica

Ligazóns externas

• "Apollonius of Perga Conics Books One to Seven" (PDF) (en inglés). Arquivado dende o orixinal (PDF) o 17 de maio de 2013. Consultado o 22 de xaneiro de 2018. 
• Hyperboloid and Asymptotic Cone, string surface model, 1872 Arquivado 15 de febreiro de 2012 en Wayback Machine. from the Science Museum