Onda estacionaria
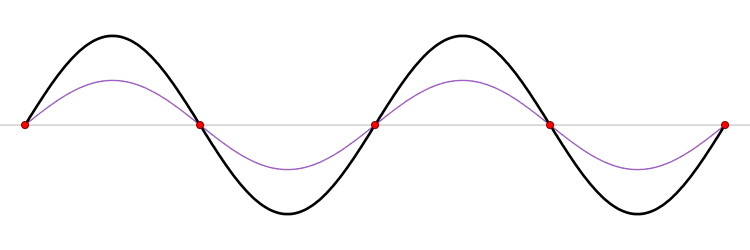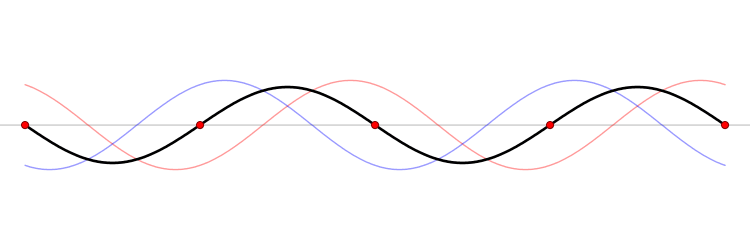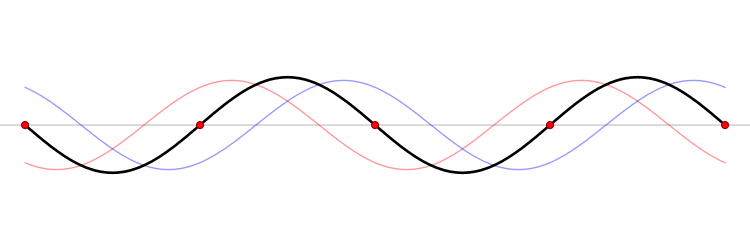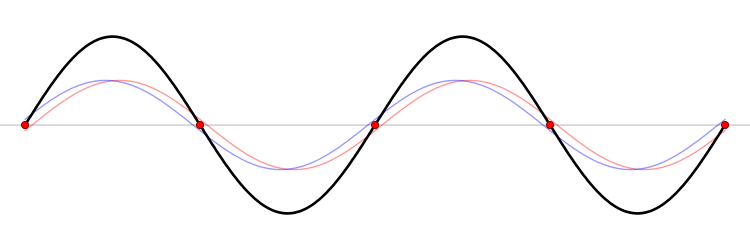
Unha onda estacionaria fórmase pola interferencia de dúas ondas da mesma natureza con igual amplitude, lonxitude de onda (ou frecuencia) que avanzan en sentido oposto a través dun medio.
Prodúcense cando interfiren dous movementos ondulatorios coa mesma frecuencia ou amplitude pero con diferente sentido, ao longo dunha liña cunha diferenza de fase de media lonxitude de onda.
As ondas estacionarias fican confinadas nun espazo (corda, tubo con aire, membrana etc.). A amplitude da oscilación para cada punto depende da súa posición, a frecuencia é a mesma para todos e coincide coa das ondas que interfiren. Hai puntos que non vibran (nodos), que permanecen inmóbiles, estacionarios, mentres que outros (ventres ou antinodos) fano cunha amplitude de vibración máxima, igual ao dobre da das ondas que interfiren, e cunha enerxía máxima. O nome de onda estacionaria provén da aparente inmobilidade dos nodos. A distancia que separa dous nodos ou dous antinodos consecutivos é media lonxitude de onda.
Pódese considerar que as ondas estacionarias non son ondas de propagación senón os distintos modos de vibración da corda, o tubo con aire, a membrana etc. Para unha corda, tubo, membrana, ... determinados, só hai certas frecuencias ás que se producen ondas estacionarias que se chaman frecuencias de resonancia. A máis baixa denomínase frecuencia fundamental, e as demais son múltiplos enteiros dela (dobre, triplo, ...).
Unha onda estacionaria pódese formar pola suma dunha onda e a súa onda reflectida sobre un mesmo eixe (x ou y).
- Cando chega a unha crista consecutiva, tendo percorrido un val.
- Viceversa.
Pódense obter pola suma de dúas ondas atendendo á fórmula:
- Sendo para x=0 e t=0, y=0, para outros casos tense que engadir o seu correspondente ángulo de desfase.
Estas fórmulas dannos como resultado:
Sendo e
Ventres e nodos[editar | editar a fonte]
- Prodúcese un ventre cando , sendo para
-
- , entón para
- Prodúcese un nodo cando , sendo para
-
- , entón para
Sendo a lonxitude da onda.
Ondas estacionarias nunha corda[editar | editar a fonte]

A formación de ondas estacionarias nunha corda débese á suma (combinación linear) de infinitos modos de vibración, chamados modos normais, os cales teñen unha frecuencia de vibración dada pola seguinte expresión (para un modo n):
Onde é a velocidade de propagación, normalmente dada por para unha corda de densidade e tensión .
A frecuencia máis baixa para a que se observan ondas estacionarias nunha corda de lonxitude L é a que corresponde a n = 1 na ecuación dos nodos (vista anteriormente), que representa a distancia máxima posible entre dous nodos dunha lonxitude dada. Esta denomínase frecuencia fundamental, e cando a corda vibra deste modo non se presentan nodos intermedios entre os seus dous extremos. A seguinte posibilidade na ecuación, o caso n = 2, chámase segundo harmónico, e presenta un nodo intermedio.
- despexamos :
Ondas estacionarias en liñas de transmisión de ondas de radio[editar | editar a fonte]
En transmisión de ondas de radio, as ondas estacionarias nas liñas de transmisión son sumamente perigosas para a integridade física dos compoñentes. Un aparato, o ROE-metro, mide a porcentaxe da onda incidente que é reflectida.
No caso ideal no que se establecera unha onda estacionaria na liña de transmisión, o transmisor acabaría destruíndose.
Unha ROE (Relación de Onda Estacionaria) de 1,5 equivale a unha reflexión do 4% da onda incidente, e admítese que é o máximo que un transmisor de 100 Watts pode soportar sen sufrir danos. En cambio, os transmisores a válvulas son menos sensibles ás ondas estacionarias.
Ondas sonoras estacionarias[editar | editar a fonte]
É un fenómeno relacionado coa reflexión do son. Dependendo de como coincidan as fases da onda incidente e reflectida, produciranse modificacións do son (aumenta a amplitude ou diminúe), polo que o son resultante pode resultar desagradable.
Cando a lonxitude da onda estacionaria é igual a unha das dimensións dunha sala (alto, ancho ou profundo), dise que a sala está en resonancia, sendo o efecto aínda máis desagradable se cabe. Hai puntos onde non chega ningún son (interferencia destrutiva) e outros onde a amplitude se dobra (interferencia construtiva). Graficamente, se se vise a onda veríase que a sinusoide desaparece e a onda adquire forma de dentes de serra. As ondas estacionarias sonoras tamén se chaman eixentonos ou modos da sala.
























