Axioma de Pasch
- Non confundir co teorema de Pasch respecto dos puntos dunha recta
En xeometría, o axioma de Pasch é un resultado da xeometría plana, foi utilizado implicitamente por Euclides, pois non pode ser derivado desde os postulados da xeometría euclidiana. O seu papel esencial foi descuberto por Moritz Pasch en 1882.[1]
Resultado[editar | editar a fonte]
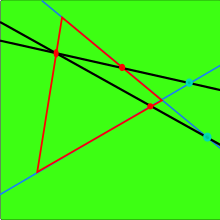
O axioma establece que,[2]
|
De feito os segmentos e non son ambos intersecados pola recta foi probado no Suplemento I,1, escrito por P. Bernays.[3]
Unha versión máis moderna deste axioma é a seguinte:[4]
|
No caso de que o terceiro lado sexa paralelo á nosa liña, contamos unha "intersección no infinito" como externa. Unha versión máis informal do axioma é a seguinte:
|
Historia[editar | editar a fonte]
Pasch publicou este axioma en 1882,[1] e mostrou que os axiomas de Euclides eran incompletos. O axioma era parte do enfoque de Pasch introducindo o concepto de orde na xeometría plana.
Equivalencias[editar | editar a fonte]
Noutros tratamentos da xeometría elemental, utilizando diferentes conxuntos de axiomas, o axioma de Pasch pode ser probado como teorema;[5] isto é unha consecuencia do axioma de separación do plano cando este é un dos axiomas. Hilbert usa o axioma de Pasch no seu tratamento axiomático da xeometría euclidiana.[6] Dados o resto de axiomas no sistema de Hilbert, pódese demostrar que o axioma de Pasch é loxicamente equivalente ao axioma de seperación do plano.[7]
O papel do axioma de Pasch en Hilbert[editar | editar a fonte]
David Hilbert utiliza o axioma de Pasch no seu libro Fundamentos da xeometría que proporciona un sistema axiomático para a xeometría euclidiana. Dependendo da edición, é numerado ben II.4 ou II.5.[6] A súa redacción foi dada máis arriba.
No sistema de Hilbert este axioma aparece na sección axiomas de orde e é etiquetado como un axioma de orde do plano. Como non se describe o axioma en termos de lados dun triángulo (considéranse rectas fronte a segmentos) non hai ningunha necesidade de falar de interseccións internas e externas da recta cos lados do triángulo .
Notas[editar | editar a fonte]
- ↑ 1,0 1,1 Pasch 1912, p. 21
- ↑ Tomado da tradución de Unger da 10ª edición de Foundations of Geometry de Hilbert, numerado II.4.
- ↑ Hilbert 1999, p. 200, tradución de Unger.
- ↑ Beutelspacher & Rosenbaum 1998, p. 7
- ↑ Wylie,Jr. 1964, p. 100
- ↑ 6,0 6,1 axiom II.5 in Hilbert's Foundations of Geometry (Townsend translation referenced below), in the authorized English translation of the 10th edition translated by L. Unger (also published by Open Court) it is numbered II.4. There are several differences between these translations.
- ↑ Só se precisan os axiomas I.1,2,3 e II.1,2,3 de Hilbert para isto. A proba dáse en Faber (1983).
Véxase tamén[editar | editar a fonte]
Bibliografía[editar | editar a fonte]
- Beutelspacher, Albrecht; Rosenbaum, Ute (1998). Projective geometry: from foundations to applications. Cambridge University Press. ISBN 978-0-521-48364-3. MR 1629468.
- Faber, Richard L. (1983). Foundations of Euclidean and Non-Euclidean Geometry. Marcel Dekker, Inc. ISBN 978-0-8247-1748-3.
- Greenberg, Marvin Jay (1974). Euclidean and Non-Euclidean Geometries: Development and History. W.H. Freeman. ISBN 978-0-7167-0454-6.
- Greenberg, Marvin Jay (2007). Euclidean and Non-Euclidean Geometries: Development and History. W.H. Freeman. ISBN 978-0-7167-9948-1.
- Hilbert, David (1903). Grundlagen der Geometrie. B.G. Teubner.
- Hilbert, David (1950). The Foundations of Geometry. Open Court Publishing.
- Hilbert, David (1999). Foundations of Geometry. Open Court Publishing. ISBN 978-0-87548-164-7.
- Moise, Edwin (1990). Elementary Geometry from an Advanced Standpoint. Addison-Wesley, Reading, MA. ISBN 978-0-201-50867-3.
- Pambuccian, Victor (2011). The axiomatics of ordered geometry: I. Ordered incidence spaces.
- Pasch, Moritz (1912). Vorlesungen uber neuere Geometrie. B.G. Teubner.
- Wylie,Jr., Clarence Raymond (1964). Foundations of Geometry. McGraw-Hill. ISBN 978-0-070-72191-3.
- Wylie,Jr., C.R. (2009). Foundations of Geometry. Dover Publications. ISBN 978-0-486-47214-0.
- Weisstein, Eric W. "Pasch's Axiom". MathWorld.




