Lonxitude

Para outras páxinas con títulos homónimos véxase: Lonxitude (homónimos).

Un paralelepípedo rectangular amosando os nomes das súas dimensións, longo, largo, e alto ou altura.

Esquema elemental de posicionamento espacial, consistente nun marco de referencia respecto a unha orixe dada.

A lonxitude é un concepto métrico definible para entidades xeométricas sobre a que se definiu unha distancia. Máis concretamente, dado un segmento, curva ou liña fina, pódese definir a súa lonxitude a partir da noción de distancia. Con todo, non debe confundirse lonxitude con distancia, xa que para unha curva xeral (non para un segmento recto) a distancia entre dous puntos calquera da mesma é sempre inferior á lonxitude da curva comprendida entre eses dous puntos. Igualmente a noción matemática de lonxitude pode identificarse coa magnitude física determinada pola distancia física.

A lonxitude é unha das magnitudes físicas fundamentais, en tanto que non pode ser definida en termos doutras magnitudes que se poden medir. En moitos sistemas de medida, a lonxitude é unha magnitude fundamental, da cal derivan outras.

A lonxitude é unha medida dunha dimensión (lineal; por exemplo a distancia en m), mentres que a área é unha medida de dúas dimensións (ó cadrado; por exemplo m²), e o volume é unha medida de tres dimensións (cúbica; por exemplo m³).

Con todo, segundo a teoría especial da relatividade (Albert Einstein, 1905), a lonxitude non é unha propiedade intrínseca de ningún obxecto dado que dous observadores poderían medir o mesmo obxecto e obter resultados diferentes (contracción de Lorentz).

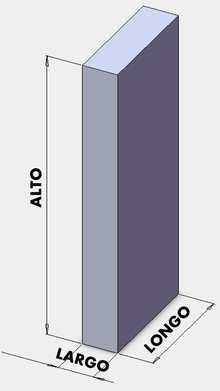
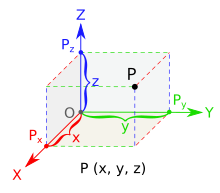
O longo ou lonxitude dimensional dun obxecto é a medida do seu eixo tridimensional y. Esta é a maneira tradicional en que se nomeaba á parte máis longa dun obxecto (en canto á súa base horizontal e non á súa altura vertical). En coordenadas cartesianas bidimensionais, onde só existen os eixos xy non se denomina «longo». Os valores x indican o ancho (eixo horizontal), e os y o alto (eixo vertical).

Véxase tamén

Bibliografía

• García Prieto, F. J. (2012). Matemáticas 2º E.S.O (en castelán). Madrid: Editex. ISBN 9788490033340. 
• Resnick, R.; Haliday, D.; Krane, K. S (1993). Física vol. 1. Título orixinal (en inglés): Physics, Vol. 1; traducido por F. Andión Uz. Compañía Editorial Continental; publicado orixinalmente por John Wiley & Sons Inc. ISBN 968-26-1230-6.