Icosaedro

Un icosaedro[1] é un poliedro de vinte caras, convexo ou cóncavo. Se as vinte caras do icosaedro son triángulos equiláteros e congruentes, iguais entre si, o icosaedro é convexo e denomínase regular, sendo entón un dos chamados sólidos platónicos. O poliedro conxugado do icosaedro é o dodecaedro.
O vocábulo icosaedro procede do grego eikosaedron, de εἴκοσι éikosi "vinte" e ἕδρα hedra "asento, cara".
Cálculo de dimensións fundamentais[editar | editar a fonte]
Raio externo[editar | editar a fonte]
Se a é a lonxitude dunha aresta dun icosaedro regular, o raio dunha esfera circunscrita (unha que toca o icosaedro en todos os seus vértices) é
Raio interno[editar | editar a fonte]
O raio dunha esfera inscrita (tanxente ás caras do icosaedro) é
Ángulo[editar | editar a fonte]
O ángulo que forman os vectores que van do centro a dous vértices adxacentes é constante e vale:
Volume, área e desenvolvemento[editar | editar a fonte]

Dado un Icosaedro regular de aresta a, pódese calcular o seu volume V mediante a seguinte fórmula:
| (Aproximadamente 2,18•a³) | |
e a área total das súas caras A (que é 20 veces a área dunha delas, Ac), mediante:
| (Aproximadamente 8,66•a²) | |
Coordenadas cartesianas e estrutura[editar | editar a fonte]
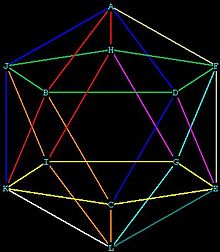
As seguintes coordenadas cartesianas definen os vértices dun icosaedro centrado na orixe:
- (0, ±1, ±φ)
- (±1, ±φ, 0)
- (±φ, 0, ±1)
Onde φ = (1+√5)/2 é a razón áurea. Cómpre salientar que os vértices dun icosaedro forman grupos de tres rectángulos áureos ortogonais entre si. O icosaedro contén no seu interior 15 rectángulos áureos: cada rectángulo contén dúas arestas opostas. Isto débese a que dous lados do rectángulo son a aresta do icosaedro e os outros dous son as diagonais de dous pentágonos regulares paralelos xirados 180 graos. A diagonal do pentágono regular está en proporción áurea co lado do pentágono, que neste caso é a aresta do icosaedro.
O icosaedro, a pesar de estar formado por 20 triángulos equiláteros, pode considerarse como a unión de 12 pentágonos regulares internos. A intersección dos pentágonos entre eles orixina as 30 arestas que conforman o icosaedro. Os 12 pentágonos regulares mencionados determinan as caras do gran dodecaedro, un dos sólidos de Kepler-Poinsot.
Proporcións áureas no icosaedro[editar | editar a fonte]
No icosaedro pódese atopar varias veces o número áureo. Na imaxe da esquerda pódense apreciar algunhas proporcións áureas presentes no icosaedro:
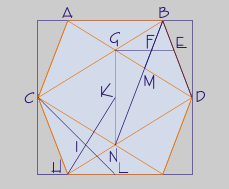
- CD/AB = φ; EG/FG = φ
- AD/GD = φ; KH/IK = φ
- GD/AG = φ; BN/MN = φ
- CL/CI = φ; AH/GN = φ
- MN/BM = φ; BM/BF = φ
- FG/EF = φ; BF/FM = φ
- IK/HI = φ; GD/MD = φ
- CI/LI = φ; MD/GM = φ
- BC/CG = φ; CG/GB = φ
Notas[editar | editar a fonte]
- ↑ Definicións no Dicionario da Real Academia Galega e no Portal das Palabras para icosaedro.







