Curva de Lorenz

Curva de Lorenz.

A curva de Lorenz é unha representación gráfica utilizada frecuentemente para plasmar a distribución relativa dunha variable nun dominio determinado. O dominio pode ser o conxunto de fogares ou persoas dunha rexión ou país, por exemplo. A variable cuxa distribución se estuda pode ser o ingreso dos fogares ou as persoas. Utilizando como exemplo estas variables, a curva trazaríase considerando no eixo horizontal a porcentaxe acumulada de persoas ou fogares do dominio en cuestión e no eixo vertical a porcentaxe acumulada do ingreso. A súa autoría é de Max O. Lorenz en 1905.

Cada punto da curva lese como porcentaxe acumulativa dos fogares ou as persoas. A curva parte da orixe (0,0) e termina no punto (100,100). Se o ingreso estivese distribuído de maneira perfectamente equitativa, a curva coincidiría coa liña de 45 graos que pasa pola orixe (por exemplo o 30% dos fogares ou da poboación percibe o 30% do ingreso). Se existise desigualdade perfecta, ou sexa, se un fogar ou persoa posuíse todo o ingreso, a curva coincidiría co eixo horizontal até o punto (100,0) onde saltaría ao punto (100,100). En xeral a curva atópase nunha situación intermedia entre estes dous extremos.

Curva de Lorenz e desigualdade

Se unha curva de Lorenz se atopa sempre por encima doutra (por tanto, está máis preto da liña de 45 graos que a outra), entón pódese dicir, sen ambigüidade, que a primeira exhibe menor desigualdade que a segunda. Esta comparación gráfica entre distribucións de distintos dominios xeográficos ou temporais é o principal emprego das curvas de Lorenz. O indicador gráfico de benestar máis usado é a Curva de Lorenz Xeneralizada (CLX), que é unha derivación da curva de Lorenz habitual. A CLX só se diferencia da de Lorenz en que na escala vertical non se representan as cantidades relativas acumuladas senón as cantidades acumuladas (non relativas) divididas polo número N de elementos da poboación. A lóxica pretendida é representar que cantidade absoluta corresponde a cada porcentaxe de individuos. Para clarificar este aspecto, supóñase que a curva de Lorenz normal dunha poboación dinos que o 50% dos menos ricos posúen o 25% da riqueza total. Pódese comprender que é moi diferente a situación de benestar deste 50% da poboación segundo se a riqueza total é moi pequena ou moi grande. É obvio que é peor posuír o 50% dunha cantidade pequena que posuír o 25% dunha cantidade moito maior. Entón dividir as cantidades acumuladas polo total de elementos N é necesario para poder comparar riquezas entre poboacións distintas que teñan un número diferente de elementos: non é o mesmo unha riqueza total de 1.000.000€ nun conxunto de 10 persoas que esa mesma riqueza total nun conxunto formado por 1.000 persoas.

Ecuación da curva de Lorenz

Se se coñece a distribución da renda como densidade de probabilidade $\scriptstyle f_{r}(r)$ para cada valor de renda, a curva de Lorenz pode calcularse analiticamente en función desta. A proporción de persoas ou unidades familiares cunha renda inferior a un nivel de renda r vén dada por:

(1) $P(r)=\int _{0}^{r}f_{r}(\rho )\ d\rho$

Mentres que a proporción de renda acumulada polas persoas con rendas iguais ou inferiores a r vén dada por:

(2) $R(r)={\frac {\int _{0}^{r}\rho f_{r}(\rho )\ d\rho }{\int _{0}^{\infty }\rho f_{r}(\rho )\ d\rho }}={\frac {1}{R_{m}}}\int _{0}^{r}\rho f_{r}(\rho )\ d\rho$

Onde $R_{m}$ é a renda media. As ecuacións (1) e (2) constitúen xuntas as ecuacións paramétricas da curva en función do parámetro r.

Propiedades

A curva de Lorenz ten pendente positiva en todos os seus puntos como se deduce da seguinte relación:

(3) $\left({\frac {dR}{dP}}\right)_{P_{0}=P(r_{0})}={\frac {\frac {dR(r_{0})}{dr}}{\frac {dP(r_{0})}{dr}}}={\frac {r_{0}f_{r}(r_{0})/R_{m}}{f_{r}(r_{0})}}={\frac {r_{0}}{R_{m}}}\geq 0$

No punto inicial $\scriptstyle r_{0}=0$ a pendente será nula, aínda que no caso $\scriptstyle f_{r}(0)=0$ o límite anterior segue sendo válido, pero no resto de puntos será estritamente positiva. Ademais a curva de Lorenz é convexa xa que a súa derivada segunda sempre é positiva:

(4) $\left({\frac {d^{2}P}{dR^{2}}}\right)_{P_{0}=P(r_{0})}={\frac {d}{dr}}\left({\frac {dR}{dP}}\right){\frac {dr}{dP}}={\frac {1}{R_{m}}}{\frac {dr(P_{0})}{dP}}={\frac {1}{R_{m}}}{\frac {1}{f_{r}(r_{0})}}\geq 0$

Exemplo 1

Nesta sección calculamos a curva de Lorenz e o índice de Gini para unha distribución de renda exponencial. Aínda que esta non parece unha distribución adecuada para a renda nacional de ningún país, a sinxeleza das expresións obtidas permite entender de modo sinxelo a aplicación das ecuacións (1) a (4). Para un país cunha renda nacional media $\scriptstyle R_{m}$ cunha distribución exponencial a densidade de probabilidade da distribución será:

$f_{r}(\rho )={\frac {1}{R_{m}}}e^{-{\frac {\rho }{R_{m}}}}$

Esta expresión permite calcular a proporción de persoas por baixo dunha certa renda e a renda acumulada dese grupo de persoas facilmente:

${\begin{cases}P=P(r)=\int _{0}^{r}{\frac {e^{-{\frac {\rho }{R_{m}}}}}{R_{m}}}d\rho =1-e^{-{\frac {r}{R_{m}}}}\\R=R(r)=\int _{0}^{r}{\frac {\rho }{R_{m}}}e^{-{\frac {\rho }{R_{m}}}}d\rho =\left(1-e^{-{\frac {r}{R_{m}}}}\right){\cfrac {r}{R_{m}}}e^{-{\frac {r}{R_{m}}}}\end{cases}}$

Despexando $\scriptstyle r$ da primeira ecuación e substituíndo o resultado na segunda obtense a curva de Lorenz explicitamente:

$R=R(P)=P+(1-P)\ln(1-P)\,$

O índice de Gini pódese calcular simplemente como:

$IG=1-2\int _{0}^{1}R(P)\ dP=0.5$

Este é o valor exacto. Cando para calcular este valor en lugar dunha distribución continua úsase un cálculo aproximado por decís en cambio resulta só $\scriptstyle IG\ \approx 0,4911$.

Exemplo 2

Índice de Gini para diferentes curvas de Lorenz asociadas a distribucións gamma .$\scriptstyle \Gamma _{n,\lambda }$ O valor de n corresponde a cada distribución, mentres que o factor $\scriptstyle \lambda$ está relacionado coa renda media e non inflúe no índice de Gini.

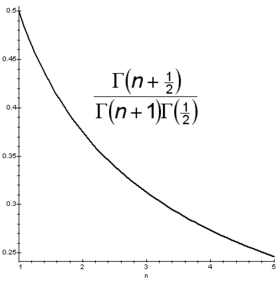
Unha aproximación máis verosímil para a renda nacional é usar en lugar dunha simple distribución exponencial, unha distribución gamma:

$f_{r}(\rho )={\frac {\lambda ^{n}}{\Gamma (n)}}\rho ^{n-1}e^{-\lambda \rho }$

Onde o parámetro $\scriptstyle \lambda$ está relacionado coa renda media mediante $\scriptstyle \lambda =n/R_{m}$. Despois dunha certa cantidade de álxebra trivial pero dificultosa pode atoparse que a proporción de persoas por baixo dunha certa renda e a renda acumulada dese grupo de persoas veñen dadas por:

${\begin{cases}P=P(r)=\int _{0}^{r}f_{r}(\rho )d\rho =1-e^{-\lambda r}P_{n-1}(\lambda r)\\R=R(r)=\int _{0}^{r}\rho f_{r}(\rho )d\rho =1-e^{-\lambda r}P_{n}(\lambda r)\end{cases}}$

Onde:

$P_{n}(x)=\sum _{k=1}^{n}{\frac {x^{k}}{k!}}=1+x+{\frac {x^{2}}{2}}+\dots +{\frac {x^{n}}{n!}}$

Neste caso non é posible despexar explicitamente $\scriptstyle r$ da primeira ecuación. Aínda que pode calcularse o índice de Gini mediante a expresión (para $\scriptstyle n$ enteiro):

$IG=1-2\int _{0}^{1}R\ dP=1-2\int _{0}^{\infty }R(r){\frac {dP(r)}{dr}}\ dr={\begin{cases}\prod _{i=1}^{n}{\frac {2k-1}{2k}}&n\in \mathbb {N} \\{\frac {\Gamma (n+1/2)}{\Gamma (n+1)\Gamma (1/2)}}&n\notin \mathbb {N} \end{cases}}$

Neste caso o coeficiente de Gini tampouco depende da renda media. Dado que o índice de Gini da maior parte de países está entre 0,50 e 0,25 a distribución gamma anterior pode usarse de maneira aproximada para reproducir a distribución real da renda.

Véxase tamén

Outros artigos

• Coeficiente de Gini
• Índice de Desenvolvemento Humano

Ligazóns externas

• La distribución de la renta, la curva de Lorenz y el índice de Gini
• Índice de Gini por países
• (en inglés) A complete handhout^{[Ligazón morta]} about the Lorenz curve including various applications, including an Excel spreadsheet graphing Lorenz curves and calculating Gini coefficients as well as coefficients of variation.