Triángulo de Reuleaux
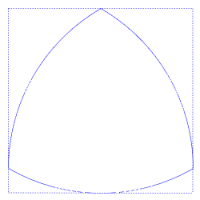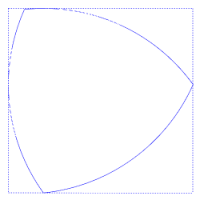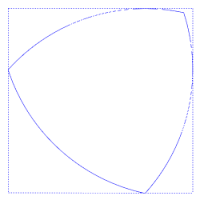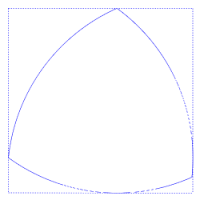
O triángulo Reuleaux é o exemplo máis sinxelo dos chamados polígonos de Reuleaux, denominados así polo científico e enxeñeiro que os desenvolveu, Franz Reuleaux. Estes polígonos teñen a particularidade de ser curvas de largura constante, é dicir, que a distancia entre dúas rectas tanxentes paralelas opostas é a mesma, independentemente da dirección desas rectas.
A área do triángulo de Reuleaux é , onde a é a largura constante. A área dun círculo de igual diámetro é , que é maior. Máis aínda, o teorema de Blaschke-Lebesgue establece que o triángulo de Reuleaux ten menor superficie que calquera outra figura de igual largura constante.
O seu perímetro é .
O triángulo de Reuleaux pode xeneralizarse a outros polígonos regulares cun número impar de lados, como pode ser o caso das moedas británicas de 20 peniques (baseadas nun heptágono).

Trazado do triángulo de Reuleaux[editar | editar a fonte]
Partindo dun triángulo equilátero de lado a delinéase facendo centro nun dos vértices do triángulo e con raio a, un arco de circunferencias que una os dous vértices restantes. Repetíndose a operación para cada vértice obtense o triángulo de Reuleaux.
Cada un dos ángulos dun triángulo equilátero é de radiáns. Cada un dos tres arcos é de lonxitude . Polo tanto o perímetro do triángulo de Reuleaux é .
Outros usos[editar | editar a fonte]

- Debido a que todos os seus diámetros teñen a mesma lonxitude, o triángulo de Reuleaux, xunto cos demais polígonos regulares de Reuleaux, é a resposta á pregunta "Ademais dun círculo, que outra forma pode ter unha tapa dun sumidoiro para que non caia a través do burato?"
- En 1914 o enxeñeiro británico Harry James Watt patentou (US-Patent 1241175 e seguintes) unha broca con forma de triángulo de Reuleaux.

- Un triángulo de Reuleaux pode rodar facilmente, pero non funciona ben como roda debido a que non ten un centro fixo de rotación.
- A existencia dos polígonos de Reuleaux demostra que unha figura que ten largura constante non implica que sexa un círculo.
- Algúns lapis se fabrican con este perfil, en lugar dos tradicionais de sección redonda ou hexagonal.[1] Polo xeral anúncianse como máis cómodos e cun agarre axeitado, ademais de ser menos probable que roden fóra das mesas.
- O rotor dun Motor Wankel pode ser confundido cun triángulo de Reuleaux. Aínda que se parece moito no seu aspecto, o rotor Wankel ten entre os vértices unha curva algo máis plana cá do triángulo de Reuleux e por iso non ten largura constante.[2]
Versión en tres dimensións[editar | editar a fonte]
A intersección de esferas de raio s centradas nos vértices de tetraedros regulares con lado tamén s denomínase tetraedro de Reuleaux, pero neste caso non é unha superficie de largura constante. Pode, non obstante, realizarse dentro dunha superficie de largura constante, coñecida como o tetraedro de Meissner, substituíndo os seus límites en forma de arco por "parches" de superficie curvada. Alternativamente, a superficie dun triángulo de Reuleaux en revolución sobre un dos seus eixes simétricos forma unha superficie de largura constante.
Notas e referencias[editar | editar a fonte]
- ↑ "Pencil Revolution". Arquivado dende o orixinal o 13 de xaneiro de 2020. Consultado o 02 de xullo de 2016.
- ↑ Ein Wankel-Rotor ist kein Reuleux-Dreieck! (en alemán)
Véxase tamén[editar | editar a fonte]
Outros artigos[editar | editar a fonte]
Ligazóns externas[editar | editar a fonte]
- Shapes of constant width (cut-the-knot)
- Mould, Steve. Shapes and Solids of Constant Width. Brady Haran. Arquivado dende o orixinal o 19 de marzo de 2016. Consultado o 02 de xullo de 2016.
- Reuleaux Triangle





