Monomorfismo

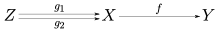
No contexto da álxebra abstracta, un monomorfismo é un homomorfismo inxectivo. Un monomorfismo de X a Y adoita denotarse coa notación $X\hookrightarrow Y$.

No marco máis xeral da teoría de categorías, un monomorfismo (tamén chamado morfismo mónico ou mono) é un morfismo cancelativo pola esquerda. É dicir, unha frecha f : X → Y tal que para todos os obxectos Z e todos os morfismos g₁, g₂: Z → X,

$f\circ g_{1}=f\circ g_{2}\implies g_{1}=g_{2}.$

produto fibrado (pullback) do monomorfismo consigo mesmo

Os monomorfismos son unha xeneralización categórica das funcións inxectivas; nalgunhas categorías as nocións coinciden, mais os monomorfismos son máis xerais, como os mostrados na sección de exemplos.

No escenario dos posets, as interseccións son idempotentes: a intersección de calquera cousa consigo mesma é ela mesma. Os monomorfismos xeneralizan esta propiedade a categorías arbitrarias. Un morfismo é un monomorfismo se é idempotente con respecto aos produtos fibrados (pullbacks).

O dual nas categorías dun monomorfismo é un epimorfismo, é dicir, un monomorfismo dunha categoría C é un epimorfismo da categoría dual C^op. Cada sección é un monomorfismo e toda retracción é un epimorfismo.

Exemplos

Todo morfismo nunha categoría concreta cuxa función subxacente é inxectiva é un monomorfismo. Na categoría de conxuntos os monomorfismos son exactamente os morfismos inxectivos. Tamén se aplica na maioría das categorías de álxebras que se producen na natureza debido á existencia dun obxecto libre nun xerador. En particular, é certo nas categorías de todos os grupos, de todos os aneis e en calquera categoría abeliana.

Non é certo en xeral, porén, que todos os monomorfismos deban ser inxectivos noutras categorías; pódese ter unha función que non sexa inxectiva e ser un monomorfismo no sentido categórico. Por exemplo, na categoría Div de grupos divisibles (abelianos) e homomorfismos de grupo entre eles hai monomorfismos que non son inxectivos: considere, por exemplo, o mapa cociente q : Q → Q/Z, onde Q son os racionais baixo adición, Z os números enteiros (tamén considerado un grupo baixo adición) e Q/Z é o grupo cociente correspondente. Este non é un mapa inxectivo, xa que, por exemplo, cada número enteiro está asignado a 0. Non obstante, é un monomorfismo nesta categoría. Isto segue da implicación q ∘ h = 0 ⇒ h = 0, que agora demostraremos. Se h : G → Q, onde G é algún grupo divisible, e q ∘ h = 0, entón h(x) ∈ Z, ∀ x ∈ G. Agora fixamos algún x ∈ G. Sen perda de xeneralidade, podemos supoñer que h(x) ≥ 0 (en caso contrario escollemos −x). Entón, sendo n = h(x) + 1, e posto que G é un grupo divisible, existe algún y ∈ G tal que x = ny, polo que h(x) = n h(y). A partir disto, e 0 ≤ h(x) < h(x) + 1 = n, despréndese que

$0\leq {\frac {h(x)}{h(x)+1}}=h(y)<1$

Dado que h(y) ∈ Z, temos que h(y) = 0, e polo tanto h(x) = 0 = h(−x), ∀ x ∈ G. Isto di que h = 0, como desexábamos.

Para pasar desa implicación ao feito de que q é un monomorfismo, subpoña que q ∘ f = q ∘ g para algúns morfismos f, g : G → Q, onde G é algún grupo divisible. Entón q ∘ (f − g) = 0, onde (f − g) : x ↦ f(x) − g(x) . (Posto que (f − g)(0) = 0 e (f − g)(x + y) = (f − g)(x) + (f − g)(y), segue que (f − g) ∈ Hom(G, Q)). Da implicación que se acaba de demostrar, q ∘ (f − g) = 0 ⇒ f − g = 0 ⇔ ∀ x ∈ G, f(x) = g(x) ⇔ f = g. Polo tanto, q é un monomorfismo, como se afirmaba.

Propiedades

• Nun topos, cada monomorfismo é un igualador, e calquera mapa que sexa tanto monomorfismo como epimorfismo é un isomorfismo.
• Todo isomorfismo é mónico.

Véxase tamén

Bibliografía

• Bergman, George (2015). An Invitation to General Algebra and Universal Constructions. Springer. ISBN 978-3-319-11478-1. 
• Borceux, Francis (1994). Handbook of Categorical Algebra. Volume 1: Basic Category Theory. Cambridge University Press. ISBN 978-0521061193. 
• "Monomorphism". Encyclopedia of Mathematics. EMS Press. 2001 [1994]. 
• Van Oosten, Jaap (1995). "Basic Category Theory" (PDF). Brics Lecture Series (BRICS, Computer Science Department, University of Aarhus). ISSN 1395-2048. 
• Tsalenko, M.S.; Shulgeifer, E.G. (1974). Foundations of category theory. Nauka. ISBN 5-02-014427-4. 

Outros artigos

• epimorfismo

Ligazóns externas

• monomorphism at the nLab
• Strong monomorphism at the nLab