Distribución t de Student

Para outras páxinas con títulos homónimos véxase: Distribución.

Distribución t de Student

Función de densidade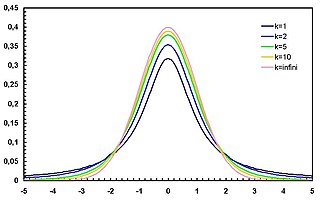
Función de distribución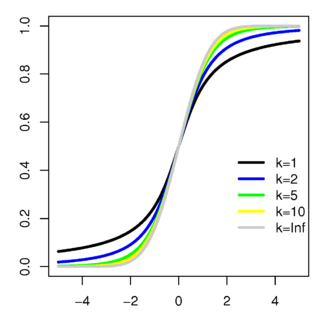
Parámetros	$\nu >0\!$ graos de liberdade (real)
Soporte	$x\in (-\infty ;+\infty )\!$
Función de densidade	${\frac {\Gamma ((\nu +1)/2)}{{\sqrt {\nu \pi }}\,\Gamma (\nu /2)}}(1+x^{2}/\nu )^{-(\nu +1)/2}\!$
Función de distribución	${\begin{matrix}{\frac {1}{2}}+x\Gamma \left({\frac {\nu +1}{2}}\right)\cdot \\[0.5em]{\frac {\,_{2}F_{1}\left({\frac {1}{2}},{\frac {\nu +1}{2}};{\frac {3}{2}};-{\frac {x^{2}}{\nu }}\right)}{{\sqrt {\pi \nu }}\,\Gamma \left({\frac {\nu }{2}}\right)}}\end{matrix}}$ onde $\,_{2}F_{1}$ é a función hiperxeométrica
Media	$0$ para $\nu >1$, indefinida para outros valores
Mediana	$0$
Moda	$0$
Varianza	${\frac {\nu }{\nu -2}}\!$ para $\nu >2$, indefinida para outros valores
Asimetría	$0$ para $\nu >3$
Curtose	${\frac {6}{\nu -4}}\!$ para $\nu >4$
Entropía	${\begin{matrix}{\frac {\nu +1}{2}}\left[\psi ({\frac {1+\nu }{2}})-\psi ({\frac {\nu }{2}})\right]\\[0.5em]+\log {\left[{\sqrt {\nu }}B({\frac {\nu }{2}},{\frac {1}{2}})\right]}\end{matrix}}$ $\psi$: función digamma, $B$: función beta
F. xeradora de momentos	(Non definida)
Func. caract.

A distribución t (de Student) é unha distribución de probabilidade que xorde do problema de estimar a media dunha poboación normalmente distribuída cando o tamaño da mostra é pequeno.

Aparece de xeito natural ao realizar a proba t de Student para a determinación das diferenzas entre dúas medias das mostras e para a construción do intervalo de confianza para a diferenza entre as medias de dúas poboacións cando se descoñece o desvío estándar dunha poboación e esta debe ser estimada a partir dos datos dunha mostra.

Caracterización

A distribución t de Student é a distribución de probabilidade do cociente

$T={\frac {Z}{\sqrt {V/\nu \ }}}=Z{\sqrt {\frac {\nu \ }{V}}}$

onde

• Z é unha variable aleatoria distribuída segundo unha normal típica (de media nula e varianza 1).
• V é unha variable aleatoria que segue unha distribución χ² con $\nu \$ graos de liberdade.
• Z e V son independentes

Se μ é unha constante non nula, o cociente ${\frac {Z+\mu }{\sqrt {V/\nu \ }}}$ é unha variable aleatoria que segue a distribución t de Student non central con parámetro de non-centralidade $\mu$.

Aparición e especificacións da distribución t de Student

Supóñase que X₁,..., X_n son variables aleatorias independentes distribuídas normalmente, con media μ e varianza σ²

Sexa

${\overline {X}}_{n}=(X_{1}+\cdots +X_{n})/n$

a media da mostra. Entón

$Z={\frac {{\overline {X}}_{n}-\mu }{\sigma /{\sqrt {n}}}}$

segue unha distribución normal de media 0 e varianza 1.

Non obstante, dado que o desvío estándar non sempre se coñece previamente, Gosset estudou un cociente relacionado,

$T={\frac {{\overline {X}}_{n}-\mu }{S_{n}/{\sqrt {n}}}},$

$S^{2}(x)={\frac {1}{n-1}}\sum _{i=1}^{n}(x_{i}-{\overline {x}})^{2}$

é a varianza da mostra e demostrou que a función de densidade de T é

$f(t)={\frac {\Gamma ((\nu +1)/2)}{{\sqrt {\nu \pi \,}}\,\Gamma (\nu /2)}}(1+t^{2}/\nu )^{-(\nu +1)/2}$

onde $\nu \$ é igual a n − 1.

A distribución de T chámase agora a distribución-t de Student.

O parámetro $\nu \$ representa o número de graos de liberdade. A distribución depende de $\nu \$, pero non de $\mu$ ou $\sigma$, o que é moi importante na práctica.

Intervalos de confianza derivados da distribución t de Student

O procedemento para o cálculo do intervalo de confianza baseado na t de Student consiste en estimar o desvío estándar dos datos S e calcular o erro estándar da media: ${\overline {X}}={\frac {S}{\sqrt {n}}}$, sendo entón o intervalo de confianza para a media: ${\overline {X}}=\pm t_{\alpha /2,n-1}{\frac {S}{\sqrt {n}}}$ .

Este resultado é o que se emprega no test de Student: posto que a diferenza das medias de mostras de dúas distribucións normais distribúese tamén normalmente, a distribución t pode empregarse para examinar se esa diferenza se pode supor razoablemente igual a cero.

Para efectos prácticos o valor esperado e a varianza son:

$E(t(n))=0$ e $Var(t(n-1))=n/(n-2)$ para $n>3$ $E(t(n))=0$ e $Var(t(n-1))=n/(n-2)$ para $n>3$ $E(t(n))=0$ e $Var(t(n-1))=n/(n-2)$ para $n>3$ $E(t(n))=0$ e $Var(t(n-1))=n/(n-2)$ para $n>3$

Historia

A distribución de Student foi descrita en 1908 por William Sealy Gosset. Gosset traballaba nunha fábrica de cervexa, Guinness, que prohibía aos seus empregados a publicación de artigos científicos debido a unha difusión previa de segredos industriais. Por ese motivo, Gosset publicou os seus resultados baixo o pseudónimo de Student (“estudante”).

Distribución t de Student non estandarizada

A distribución t pode xeralizarse a 3 parámetros, introducindo un parámero locacional $\mu$ e outro de escala $\sigma$. O resultado é unha distribución t de Student non estandarizada cunha densidade que está definida por:

$p(x|\nu ,\mu ,\sigma )={\frac {\Gamma ({\frac {\nu +1}{2}})}{\Gamma ({\frac {\nu }{2}}){\sqrt {\pi \nu }}\sigma }}\left(1+{\frac {1}{\nu }}\left({\frac {x-\mu }{\sigma }}\right)^{2}\right)^{-{\frac {\nu +1}{2}}}$

Equivalentemente, pode escribirse en termos de $\sigma ^{2}$ (correspondente á varianza en vez de ao desvío estándar):

$p(x|\nu ,\mu ,\sigma ^{2})={\frac {\Gamma ({\frac {\nu +1}{2}})}{\Gamma ({\frac {\nu }{2}}){\sqrt {\pi \nu \sigma ^{2}}}}}\left(1+{\frac {1}{\nu }}{\frac {(x-\mu )^{2}}{\sigma ^{2}}}\right)^{-{\frac {\nu +1}{2}}}$

Outras propiedades desta versión da distribución t son:

${\begin{aligned}\operatorname {E} (X)&=\mu \quad \quad \quad {\text{para }}\,\nu >1,\\{\text{Var}}(X)&=\sigma ^{2}{\frac {\nu }{\nu -2}}\,\quad {\text{para }}\,\nu >2,\\{\text{Moda}}(X)&=\mu .\end{aligned}}$

Véxase tamén

Ligazóns externas

• Tabla de distribución de t de Student
• Prueba t de Student na UPTC de Colombia
• Distribución t-Student: Puntos porcentuais para probabilidade superior
• Cálculo da probabilidade dunha distribución t de Student con R (linguaxe de programación)