Diagrama de Euler

Diagrama de Euler que ilustra que o conxunto de "animais con catro patas" é un subconxunto de "animais", mais o conxunto de "minerais" é un conxunto disxunto (non ten membros en común) con "animais".

Un diagrama de Euler é semellante a un diagrama de Venn, mais non precisa conter todas as zonas (onde unha zona se define como a área de intersección entre dous ou máis contornos). Así, un diagrama de Euler pode definir un universo de discurso, é dicir, pode definir un sistema no que certas interseccións non son posíbeis nin consideradas.

Así, un diagrama de Venn que conteña os atributos de Animal, Mineral e Catro patas tería que conter interseccións onde algúns estean tanto en Animal, Mineral e Catro patas. En consecuencia, un diagrama de Venn mostra todas as combinacións ou conxuncións posíbeis.

Diagrama de Euler de tipos de obxectos celestes

Introdución

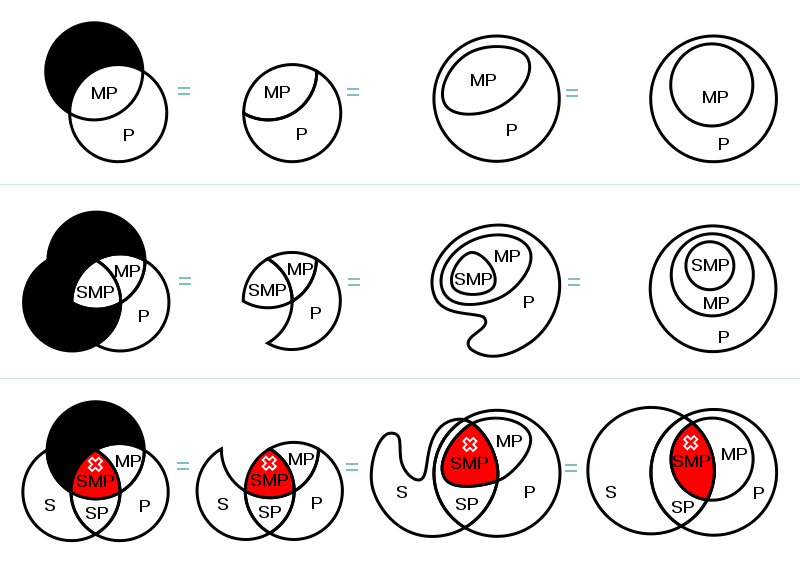
Os diagramas de Euler consisten en curvas pechadas simples (xeralmente círculos) no plano que mostra os conxuntos. Os tamaños e as formas das curvas non son importantes: o significado do diagrama reside na forma en que se superpoñen. As relacións espaciais entre as rexións delimitadas por cada curva (superposición, contención ou ningunha) corresponden a relacións teóricas (subconxunto intersección e disxunción).

Cada curva de Euler divide o plano en dúas rexións ou zonas: a interior, que representa simbolicamente os elementos do conxunto, e a exterior, que representa todos os elementos que non son membros do conxunto. As curvas cuxos interiores non se cruzan representan conxuntos disxuntos. Dúas curvas cuxos interiores se cruzan representan conxuntos que teñen elementos comúns, a área dentro de ambas as curvas representa o conxunto de elementos comúns a ambos os conxuntos (intersección dos conxuntos). Unha curva que está contida completamente dentro da zona interior doutra representa un subconxunto desta.

Os diagramas de Venn son unha forma máis restritiva dos diagramas de Euler. Un diagrama de Venn debe conter todas as zonas posíbeis de superposición entre as súas curvas, representando todas as combinacións de inclusión/exclusión dos seus conxuntos constituíntes, mais nun diagrama de Euler algunhas zonas poden faltar. Esta falta foi o que motivou a Venn a desenvolver os seus diagramas.

Había que crear diagramas nos que se puidese observar, mediante suposicións, calquera relación entre as zonas, non só as que sexan "verdadeiras".

Galería

Véxase tamén

Bibliografía

• Couturat, Louis (1914). The Algebra of Logic: Authorized English Translation by Lydia Gillingham Robinson with a Preface by Philip E. B. Jourdain. Chicago and London: The Open Court Publishing Company.  Modelo:Sfn whitelist
• Sir William Hamilton (1860). Mansel, Henry Longueville; Veitch, John, eds. Lectures on Metaphysics and Logic. Edinburgh and London: William Blackwood and Sons. 
• Jevons, W. Stanley (1880). Elementary Lessons in Logic: Deductive and Inductive. With Copious Questions and Examples, and a Vocabulary of Logical Terms. London and New York: M. A. MacMillan and Co. 
• Karnaugh, Maurice (novembro 1953) [1953-04-23, 1953-03-17]. "The Map Method for Synthesis of Combinational Logic Circuits" (PDF). Transactions of the American Institute of Electrical Engineers, Part I: Communication and Electronics 72 (5): 593–599. doi:10.1109/TCE.1953.6371932. Paper 53-217. Arquivado dende o orixinal (PDF) o 2017-04-16. Consultado o 2017-04-16. 
• Sandifer, Ed (xanueiro 2004). "How Euler Did It" (PDF). maa.org. Arquivado dende o orixinal (PDF) o 2013-01-26. 

• Veitch, Edward Westbrook (1952-05-03) [1952-05-02]. "A chart method for simplifying truth functions". Proceedings of the 1952 ACM national meeting (Pittsburgh) on - ACM '52. New York, USA: Association for Computing Machinery. pp. 127–133. doi:10.1145/609784.609801. 

Outros artigos

• Diagrama de Venn.

Ligazóns externas

• Euler Diagrams. Brighton, UK (2004).What are Euler Diagrams?