Relación simétrica
Unha relación simétrica é un tipo de relación binaria. Formalmente, unha relación binaria R sobre un conxunto X é simétrica se: [1]
aquí a notación aRb significa que (a, b) ∈ R .
| Relacións binarias transitivas | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Todas as definicións requiren tacitamente que a relación homoxénea sexa transitiva: para todo se e entón |
A simetría, xunto coas relacións de reflexividade e a de transitividade, son as tres propiedades que definen unha relación de equivalencia.[1]
Exemplos
[editar | editar a fonte]En matemáticas
[editar | editar a fonte]- "é igual a" (igualdade) (mentres que "é menor que" non é simétrica)
- "é comparable a", para elementos dun conxunto parcialmente ordenado
- "x e y son impares":
Fóra das matemáticas
[editar | editar a fonte]- "está casado con"
- "é un irmán totalmente biolóxico de"
- "é un compañeiro de traballo"
Asimétrica
[editar | editar a fonte]Asimétrica. Cando unha relación é o oposto a unha simétrica, é dicir, cando se dá que se un elemento está relacionado con outro mediante R, entón ese outro non está relacionado co primeiro, entón se di que é asimétrica, o que denotamos formalmente por:
Neste caso, dise que R cumpre coa propiedade de asimetría.
Antisimétrica
[editar | editar a fonte]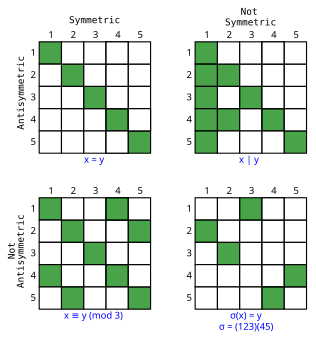
Antisimétrica. Unha relación binaria sobre un conxunto é antisimétrica cando se dá que se dous elementos de relaciónanse entre si mediante , entón estes elementos son iguais.
É dicir,
Nese caso, dise que cumpre coa propiedade de antisimetría.
| Simétrica | Non simétrica | |
| Antisimétrica | Igualdade. | 1.Divide. 2.Menor ou igual a. |
| Non antisimétrica | Congruencia en aritmética modular. | 1.División enteira.
2.A maioría das permutacións non triviais. |
Notas
[editar | editar a fonte]- ↑ 1,0 1,1 Biggs, Norman L. (2002). Discrete Mathematics. Oxford University Press. p. 57. ISBN 978-0-19-871369-2.
Véxase tamén
[editar | editar a fonte]| Wikimedia Commons ten máis contidos multimedia na categoría: Relación simétrica |
Outros artigos
[editar | editar a fonte]




















