Leis de Kirchhoff
Este artigo precisa de máis fontes ou referencias que aparezan nunha publicación acreditada que poidan verificar o seu contido, como libros ou outras publicacións especializadas no tema. Por favor, axude mellorando este artigo. (Desde febreiro de 2018.) |
As Leis (ou Lemas) de Kirchhoff foron formuladas por Gustav Kirchhoff no ano 1845, mentres aínda era un estudante. Empreganse moito en enxeñería eléctrica para obter os valores de intensidade de corrente e potencial en cada punto dun circuíto eléctrico. Xorden da aplicación da lei de conservación da enerxía.
En circuítos complexos, así coma en aproximacións de circuítos dinámicos, pódense aplicar empregando un algoritmo sistemático, sinxelamente programable en sistemas de cálculo informatizado mediante matrices, así coma aproximacións de circuítos dinámicos.
Definicións
[editar | editar a fonte]- Para o seu enunciado é necesario previamente definir os conceptos de malla e de nodo:
- Malla ou lazo é o circuíto que resulta de percorrer o esquema eléctrico nun mesmo sentido regresando ao punto de partida, pero sen pasar dúas veces pola mesma rama.
- Nó ou nodo é o punto onde concorren varias ramas dun circuíto. O sentido das correntes é arbitrario e debe asignarse previamente ao planteo do problema.
- Rama é o fragmento de circuíto eléctrico comprendido entre dous nodos.
Enunciado das Leis
[editar | editar a fonte]Lei dos nós ou lei de correntes de Kirchhoff
[editar | editar a fonte]
(KCL - Kirchhoff's Current Law - nas súas siglas en inglés ou LCK, lei de corrente de Kichhoff, en galego)
- En todo nó, onde a densidade da carga non varíe nun instante de tempo, a suma de correntes entrantes é igual á suma de correntes saíntes.
Un enunciado alternativo é:
- en todo nó a suma alxébrica de correntes debe ser 0.
Lei das mallas ou lei de tensións de Kirchhoff
[editar | editar a fonte]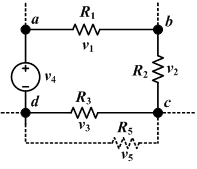
(KVL - Kirchhoff's Voltage Law - nas súas siglas en inglés ou LVK, Lei de voltaxe de Kirchhoff en galego)
- En toda malla a suma de tódalas caídas de tensión é igual á suma de tódalas forzas electromotrices.
Un enunciado alternativo é:
- en toda malla a suma alxébrica das diferenzas de potencial eléctrico debe ser cero.


