Proporcionalidade (matemáticas)

A proporcionalidade é unha relación entre magnitudes. É un dos escasos conceptos matemáticos amplamente difundidos entre a poboación debido a que é en boa medida unha noción intuitiva e de uso moi común.

A proporcionalidade directa é un caso particular das variacións lineais.

O factor constante de proporcionalidade pode utilizarse para expresar as relacións entre as magnitudes.

Símbolo

O símbolo matemático '∝' utilízase para indicar que dous valores son proporcionais. Por exemplo, A ∝ B.

En Unicode este é o símbolo: U+221D.

Exemplos

Primeiro exemplo

A receita dunha torta de vainilla indica que para catro persoas necesítanse 200 g de fariña, 150 g de manteiga, catro ovos e 120 g de azucre vainillado. Como adaptar a receita para cinco persoas? Segundo varios estudos, a maioría da xente calcularía as cantidades para unha persoa (dividindo entre catro) e logo as multiplicaría polo número real de persoas, cinco; outras só lle sumarían o que a unha persoa lle corresponde. Unha minoría non sente a necesidade de pasar polas cantidades unitarias (é dicir, por persoa) e multiplicaría os números da receita por 5/4 = 1,25 (o que equivale a engadir cinco ovos, 250 g de fariña, 187,5 g de manteiga e 150 g de azucre), e a torta terá o mesmo sabor que a outra, se o cociñeiro afeccionado é tan bo como o chef que escribiu a receita.

Dise que a cantidade de cada ingrediente é proporcional ao número de persoas, e se representa esta situación mediante unha táboa de proporcionalidade: coeficiente k non nulo ($5 \over 4$ no exemplo) tal que

$y_{1}=k\cdot x_{1},y_{2}=k\cdot x_{2}\quad ...\quad y_{n}=k\cdot x_{n}\$

Variábeis proporcionais relacionadas por unha función lineal.

Se consideramos $x_{1},x_{2}...x_{n}\$ e $y_{1},y_{2}...y_{n}\$ como valores de variábeis $x\$ e $y\$, entón dise que estas variábeis son proporcionais; a igualdade y = k·x significa que y é unha función lineal de x.

A representación gráfica desta función é unha recta que pasa pola orixe do sistema de coordenadas. Unha variación (incremento ou decremento) de x dá lugar a unha variación proporcional de y (e reciprocamente, posto que k≠0: e = 1/k · x):

$\Delta y=k\cdot \Delta x\$

Son as funcións máis sinxelas que existen e as primeiras que se estudan na clase de matemáticas, con alumnos de trece anos aproximadamente.

A relación "Ser proporcional a" é

• reflexiva (toda variábel es proporcional a si mesma, co coeficiente 1)
• simétrica (cando y é proporcional a x entón x o é a y, co coeficiente inverso) e
• transitiva (se x é proporcional a y, e y a z, entón x o é con z, multiplicando os coeficientes)

polo que se trata dunha relación de equivalencia. En particular dúas variábeis proporcionais a unha terceira serán proporcionais entre si).

A táboa do primeiro exemplo pódese descompoñer en tres de formato dous por dous:

Tres táboas de proporcionalidade 2x2.

por tanto as propiedades da proporcionalidade ilústranse preferentemente con táboas de catro cuadrículas.

Tres maneiras de ver a proporcionalidade.

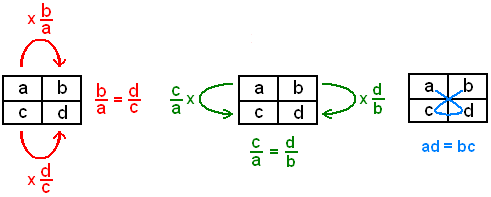
Unha proporción está formada polos números a, b, c e d, se a razón entre a e b é a mesma que entre c e d.

Unha proporción está formada por dúas razóns iguais: a : b = c : d

Onde a, b, c e d son distintos de cero e lese a é a b como c é a d .

Proporción múltipla:

Unha serie de razóns está formada por tres ou máis razóns iguais: a : b = c : d = e : f

E pode expresarse como unha proporción múltipla: a : c : e = b : d : f

Na proporción hai catro termos; a e d denomínase extremos; c e b chámanse medios.

En toda proporción o produto dos extremos é igual ao produto dos medios.

Para establecer que unha táboa é proporcional, pódese:

1. verificar que a segunda columna é múltiplo da primeira, (primeira táboa: para pasar do primeiro cadro ao segundo, hai que multiplicar por $b \over a$; na segunda liña tense que multiplicar por $d \over c$, logo estas fraccións deben ser iguais para obter columnas proporcionais)
2. verificar que a segunda liña es múltiplo da primeira (segunda táboa, cun razoamento parecido) ou
3. verificar a igualdade dos produtos cruzados: a·d = b·c. (terceira táboa: as igualdades anteriores equivalen a a·d = b·c, cando non hai valores nulos, que por certo non teñen un grande interese neste contexto).

Segundo exemplo

Dous albaneis constrúen un muro de doce metros de superficie en tres horas; que superficie construirán cinco albaneis en catro horas?

Hai dous parámetros que inflúen na superficie construída: o número de albaneis e o tempo de traballo. Non hai que resistir a tentación de aplicar dúas veces a proporcionalidade pero, iso si, explicitando as hipóteses subxacentes.

Afirmar que o traballo realizado é proporcional ao número de albaneis equivale a dicir que todos os obreiros teñen a mesma eficacia no traballo (son intercambiábeis); e afirmar que a superficie á proporcional ao tempo de traballo supón que o rendemento non cambia co tempo: os albaneis non se cansan.

Proporcionalidade múltipla.

Admitindo estas dúas hipóteses, pódese contestar á pregunta pasando por unha etapa intermedia: que superficie construirían dous albaneis en catro horas?

O parámetro "número de albaneis" ten un valor fixo, logo aplicamos a proporcionalidade co tempo (subtáboa vermella). A superficie construída será multiplicada por $4 \over 3$. Logo, fixando o parámetro tempo en catro horas, e variando o número de obreiros de 2 a 5, a superficie se multiplicará por $5 \over 2$ (a subtáboa azul é proporcional).

O resultado final é

$12\times {\frac {4}{3}}\times {\frac {5}{2}}=40$

metros cadrados.

A proporcionalidade múltipla resólvese así, multiplicando polos coeficientes correspondentes a cada factor:

Caso xeral da proporcionalidade múltipla.

Terceiro exemplo

Dous autos percorren exactamente o mesmo camiño. O primeiro tardou dúas horas e media en chegar ao destino, rodando a unha velocidade media de 70 km/h. O segundo roda a 100 km/h. Canto tempo tardará en chegar?

Canto maior sexa a velocidade, menor tempo durará a viaxe. Se multiplicamos por dous a velocidade, a duración da viaxe se dividirá por dous. Aquí, claramente o tempo do percorrido non é proporcional á velocidade senón xustamente o contrario: é inversamente proporcional, é dicir, proporcional á inversa da velocidade. Isto permite responder á pregunta:

Exemplo de proporcionalidade inversa.

cambiando unha multiplicación por unha división (primeira táboa) ou aplicando a proporcionalidade coa inversa da velocidade (segunda táboa). O tempo será $2,5\times {\frac {7}{10}}=1,75$, é dicir, unha hora e 45 minutos.

Máis xeralmente, se unha variábel y é inversamente proporcional a outra variábel x, pódese aplicar a proporcionalidade con $1 \over x$, ou máis ben utilizar a seguinte equivalencia:

Método para a proporcionalidade inversa.

É dicir, que o produto dos valores correspondentes (aquí na mesma liña) é constante. No exemplo: 70 × 2,5 = 100 × 1, 75 = 175 km, que é a lonxitude do percorrido.

Táboa de variación proporcional

Unha táboa de variación proporcional é aquela que segue unha secuencia utilizando de base o prezo dalgún obxecto ou outra cousa que poida aumentar ou diminuír certo número ou obxecto de forma proporcional.

Exemplo:

nº de bólas / prezo

2 bólas / 50 céntimos

4 bólas / 1 euro

6 bólas / 1,50 euros

Magnitudes directamente proporcionais

Dúas magnitudes son directamente proporcionais cando ao multiplicar ou dividir unha delas por un número, a outra queda multiplicada ou dividida respectivamente polo mesmo número.

Exemplo:

Un automóbil consome 10 litros de gasolina por cada 120 km de percorrido. Cantos quilómetros percorre con 30 litros?

Observamos que as magnitudes son directas. Se a razón ou cociente entre elas é un valor constante. Cos datos da táboa, achamos a razón.

Elaboramos unha táboa de proporcionalidade:

Gasolina 10 1 10 20 40

(litros)

Percorrido 120 12 240 480

(quilómetros)

Con 20 litros de gasolina, o coche percorre 240 quilómetros: cantos máis quilómetros se percorran, máis litros de gasolina se consumirán. O número de quilómetros percorridos é directamente proporcional (D.P.) ao número de litros de gasolina, sempre que as demais condicións se manteñan constantes, isto é, que non se modificaran as condicións climáticas ou xeográficas que modificaran o consumo. Polo tanto, con 30 litros de gasolina o coche percorrerá 360 quilómetros.

Aplicación en xeometría

O concepto de proporcionalidade é equivalente ao de semellanza cando se comparan dous triángulos semellantes. De feito, as propiedades da proporcionalidade (reflexividade, simetría e transitividade) son as mesmas que as da semellanza.

Véxase tamén

Outros artigos

• Eudoxo de Cnido.
• Número áureo.
• Triángulo.

Ligazóns externas

• Wolfram MathWorld (en inglés).