Matemáticas e arte

As matemáticas na arte: gravado sobre placa de cobre de Albrecht Dürer (Durero) Melancolía I, 1514. As referencias inclúen un compás para a xeometría, un cadrado máxico e un romboedro truncado, mentres a medición está indicada polas escalas e o reloxo de area.

Debuxo precursor dos Wireframe dun vaso como sólido de revolución, obra de Paolo Uccello. S. XV

As matemáticas e a arte están relacionadas de varios xeitos. É frecuente atopar as matemáticas descritas como unha arte debido á beleza ou elegancia das súas formulacións, e pódese atopar a súa presenza na música, danza, pintura, arquitectura, escultura, artes téxtiles, cine...

Os vínculos de ambas as disciplinas son múltiples e moi diversos, desde o uso de patróns xeométricos, módulos e redes, ás aplicacións da perspectiva, creación ou corrección de ilusións ópticas (desde as columnas gregas ao Op-Art), o uso de distintas medicións con uso de aparellos tecnolóxicos que foron posíbeis grazas ao desenvolvemento das matemáticas (lentes, aplicacións do láser etc.), até o feito de que as matemáticas foron determinantes en varias vangardas do século XX.

Este artigo céntrase na influencia das matemáticas nas artes visuais, máis do que a análise das obras de arte en base ás matemáticas. En 2006 un estudo afirmou que as pinceladas das estrelas e o ceo pintados en xuño de 1889 por Vincent van Gogh no seu cadro A noite estrelecida se axustan á ecuación de turbulencias creada en 1941 por Andrei Kolmogorov. Van Gogh era afeccionado á astronomía e mesmo procuraba explicacións científicas do cromatismo das estrelas, porén non cabe inferir unha influencia directa das teorías das turbulencias nesta obra.

As matemáticas e a arte teñen longa relación histórica, desde os principios da historia da arte até artistas recentes como Liz Paley. Está documentada a existencia de artistas matemáticos desde o século IV a.C., cando o escultor grego Policleto escribiu o seu Canon, prescribindo proporcións baseadas na relación $1:{\sqrt {2}}$ para o espido masculino ideal. Curiosamente, cada vez son máis frecuentes presuntas evidencias do uso do número áureo na arte e a arquitectura antigas, aínda que sen bases fiables que apoien as teorías. Mesmo algunhas obras poden ter relación casual e non causal coa proporción áurea. No Renacemento italiano, Luca Pacioli escribiu o influente tratado De divina proportione (1509), ilustrado con xilogravuras de Leonardo da Vinci, sobre o uso da proporción áurea na arte. Outro italiano, Piero della Francesca, desenvolveu as ideas de Euclides sobre a perspectiva en tratados como De Prospectiva Pingendi e nas súas propias pinturas. O gravador Dürer efectuou numerosas referencias ás matemáticas na súa obra. Nos tempos modernos, o artista gráfico M. C. Escher fixo un uso intensivo do teselado e da xeometría hiperbólica coa axuda do matemático Harold Scott MacDonald Coxeter, mentres que o movemento De Stijl liderado por Theo van Doesburg e Pieter Mondrian abarcou explicitamente as formas xeométricas. As matemáticas inspiraron tamén as artes téxtiles de teares, alfombras e outras creacións. Na arte islámica, as simetrías son evidentes en formas tan variadas como o girih persa e o azulexo zellige< marroquí, as bóvedas decoradas etc.

O influxo directo das matemáticas sobre a arte evidénciase no uso de ferramentas como a perspectiva, a análise da simetría, ou a presenza en diversas obras de obxectos matemáticos que exerceron atracción sobre artistas de distintas épocas, como os poliedros (en pinturas e debuxos de Dürer, Marcus Wenninger, Wenzel Jamnitzer, Lorenz Stoer, Giorgio de Chirico e outros, e por suposto na escultura e na arquitectura), ou a banda de Möbius descuberta de maneira independente polos matemáticos August F. Möbius e J. Benedict Listing, e polo escultor Max Bill, quen pensou ser o primeiro en describir a forma.

Conceptos matemáticos como a recursividade e paradoxos lóxicos pódense ver nas pinturas de René Magritte e en gravados do citado M. C. Escher. A arte computacional a miúdo fai uso de fractais, incluído o conxunto de Mandelbrot, e ás veces, explora obxectos matemáticos como os autómatas celulares. De forma controvertida, ligando a óptica coa pintura, o artista David Hockney argumentou que desde o Renacemento en diante a maioría dos artistas utilizaron a cámara lúcida para debuxar representacións precisas de escenas; e o arquitecto Philip Steadman argumentou de maneira similar que Johannes Vermeer usou a cámara escura na composición das súas pinturas.

Outras relacións inclúen a análise algorítmica das obras de arte mediante a fluorescencia de raios X, ou o achado de que os batik tradicionais de diferentes rexións da illa de Xava teñen composicións fractais. A arte serviu en ocasións como estímulo para a investigación matemática, especialmente no caso da teoría da perspectiva de Filippo Brunelleschi, que finalmente levou a Girard Desargues ao desenvolvemento da xeometría proxectiva. Unha visión persistente, baseada en última instancia na noción pitagórica da harmonía musical, sostén que o universo está organizado segundo relacións numéricas, que Deus é o xeómetra do mundo e que, por tanto, a xeometría é sacra, tal como se reflicte en obras de arte como O ancián dos días de William Blake.

Orixes: desde a antiga Grecia até o Renacemento

Canon e simetría de Policleto

Copia romana en mármore do Doríforo de Policleto.

Artigo principal: Policleto.

Policleto (c. 450–420 a.C.) foi un escultor grego da escola de Argos. A temática das súas obras consistía principalmente en atletas. Segundo o matemático Xenócrates, Policleto foi un dos escultores máis importantes da Antigüidade polo seu traballo no Doríforo e na estatua de Hera. As súas esculturas poden non ser tan famosas como as de Fidias, pero tamén foron moi admiradas. No seu Canon, un tratado que escribiu para documentar as proporcións "perfectas" da anatomía do espido masculino introduciu un enfoque matemático para esculpir o corpo humano.

Utilizaba a lonxitude da falanxeta do maimiño da man de módulo básico para determinar as proporcións do corpo humano. Multiplicaba a súa lonxitude por ${\sqrt {2}}$ para obter a distancia da segunda falanxe (falanxina) e multiplicaba a lonxitude novamente por ${\sqrt {2}}$ para obter a lonxitude da terceira falanxe. A continuación, tomaba a lonxitude dese dedo e multiplicábaa por ${\sqrt {2}}$ para obter a lonxitude da palma desde a base do dedo até o cúbito. Esta serie xeométrica de medidas avanza até formar o brazo, o tórax e o corpo completo con todas as súas partes.

A influencia do Canon de Policleto é inmensa na escultura da antiga Grecia, Roma e o Renacemento, e numerosos escultores seguiron as súas prescricións. Aínda que non se conserva ningunha das súas obras orixinais, as copias romanas mostran o seu canon ideal e a súa precisión matemática. Algúns estudosos argumentan que o pensamento pitagórico influíu en Policleto, aplicando os conceptos matemáticos básicos da xeometría grega, como a relación, a proporción e a simetría (en grego significa "harmonía nas proporcións") e convérteos nun sistema capaz de describir a forma humana a través dunha serie de series xeométricas continuas.

Perspectiva e proporción

Artigo principal: Perspectiva (gráfica).

Experimento de Brunelleschi sobre a perspectiva.

Na Antigüidade clásica, en vez de axustar o tamaño das figuras dunha composición de acordo coa súa distancia ao observador (segundo as regras da perspectiva), os pintores establecían o tamaño de obxectos e figuras segundo a súa importancia temática. Na Idade Media, algúns artistas usaron a perspectiva invertida para salientaren determinados motivos. O matemático musulmán Alhazen (Ibn al-Haytham), describiu unha teoría xeométrica da óptica no seu Libro de Óptica en 1021, e aínda que non a aplicou á arte, influíu en artistas e científicos posteriores, chegando a ser considerado un dos pais do método científico. O Renacemento viu o rexurdir das ideas gregas e romanas clásicas na cultura, incluído o estudo das matemáticas para comprender a natureza e a arte. Dous motivos principais levaron os artistas de finais da Idade Media e do Renacemento cara ás matemáticas: en primeiro lugar, os pintores necesitaban descubrir como representar escenas tridimensionais nun lenzo bidimensional; e en segundo lugar, tanto os filósofos como os artistas estaban convencidos de que as matemáticas eran a esencia do mundo físico e que todo o universo, incluídas as artes, se podía explicar en termos numéricos.

Os rudimentos da perspectiva chegaron con Giotto (1266/7-1337), que tentou debuxar usando un método alxebraico para determinar as localización das liñas distantes. En 1415, o arquitecto italiano Brunelleschi e o seu amigo Alberti demostraron en Florencia o método necesario para aplicar a perspectiva, utilizando o principio de semellanza tal como o formulou Euclides para determinar a altura aparente de obxectos distantes. Aínda que se perderon as pinturas de Brunelleschi, os frescos de Masaccio da Santísima Trindade mostran os seus principios.

O pintor italiano Paolo Uccello (1397-1475) estaba fascinado pola perspectiva, como mostran as súas pinturas da Batalla de San Romano (c. 1435–1460): as lanzas rotas converxen segundo liñas de perspectiva.

O pintor Piero della Francesca (c. 1415–1492) exemplificou este cambio no pensamento do Renacemento italiano, axuntando a súa condición de artista coa de experto matemático e xeómetra, autor de libros sobre espazo xeométrico e perspectiva, incluíndo De Prospectiva pingendi (Sobre a perspectiva para pintar), Trattato d'Abaco (Tratado do Ábaco), e De corporibus regularibus (Sobre os Sólidos Regulares).

O historiador Vasari na súa obra Le vite de' più eccellenti pittori, scultori e architettori chámao o "xeómetra máis grande do seu tempo, ou quizais de calquera época". O interese de Piero della Francesca pola perspectiva pódese ver en pinturas súas coma o Políptico de San Antonio, o Retablo de Santo Agostino e Cristo na columna. O seu traballo influíu en matemáticos e artistas posteriores, como en Luca Pacioli na súa obra De divina proportione, e en Leonardo da Vinci. Estudou matemáticas clásicas e os traballos de Arquímedes, e aprendeu aritmética comercial en "escolas do ábaco". O formato dos seus escritos lembra ao dos libros de texto da escola do ábaco, seguindo moi posiblemente o estilo do Liber abaci, publicado en 1202 por Leonardo de Pisa (coñecido como Fibonacci). Alberti explicou no seu tratado de 1435 De pictura que: "Os raios de luz viaxan en liña recta desde os puntos na escena observada até o ollo, formando unha especie de pirámide co ollo como vértice". Unha pintura construída mediante a perspectiva lineal é unha sección transversal desa pirámide.

En De Prospectiva Pingendi, Piero transformou as súas observacións empíricas da forma en que os aspectos dunha figura cambian co punto de vista, en probas matemáticas. O seu tratado parte do traballo de Euclides: define o punto como "a cousa máis pequena que o ollo comprende". Utiliza o razoamento dedutivo para guiar o lector á representación en perspectiva dun corpo tridimensional.

O artista David Hockney argumentou no seu libro Secret Knowledge: Rediscovering the lost techniques of the Old Masters que os artistas comezaron a usar unha cámara lúcida a partir da década de 1420, o que deu como resultado un cambio repentino na precisión e no realismo en moi pouco tempo, e que esta práctica foi continuada polos principais artistas, incluídos Ingres, Van Eyck e Caravaggio. Os críticos non se poñen de acordo sobre se a tese de Hockney é correcta ou non. Do mesmo xeito, o arquitecto Philip Steadman argumentou tamén con controversia que Johannes Vermeer usara un dispositivo diferente, unha cámara escura, para axudalo a crear as súas pinturas.

Rombicuboctaedro oco en perspectiva, obra de Leonardo.

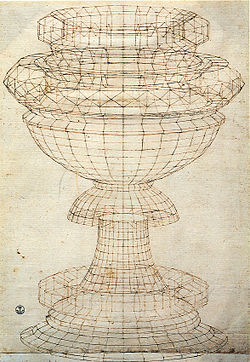
En 1509, Luca Pacioli (c. 1447-1517) publicou De divina proportione sobre a relación das matemáticas e a arte a través da proporción, abordando mesmo por este método cuestións como a representación do rostro humano. Leonardo da Vinci (1452–1519) ilustrou o texto con gravados de sólidos regulares mentres estudaba con Pacioli na década de 1490. Os debuxos de Leonardo son probablemente as primeiras ilustracións realistas de sólidos xeométricos reducidos a un armazón de arestas. Figuras como o rombicuboctaedro foron das primeiras a ser debuxadas así para mostrar a perspectiva mediante a superposición das arestas en primeiro plano sobre as do fondo, que podían á súa vez verse polos ocos das caras. O traballo discute a perspectiva nos traballos de Piero della Francesca, Melozzo dá Forlì e Marco Palmezzano.

Da Vinci estudou a Summa de Pacioli, da que copiou as táboas de proporcións. Na Gioconda e na Última Cea, incorporou unha perspectiva lineal cun punto de fuga para obter unha aparencia de profundidade. A Última Cea ideouse cunha proporción estreita de 12:6:4:3, do mesmo xeito que a A escola de Atenas de Rafael inclúe a Pitágoras cunhas táboas de proporcións ideais, sacras para os pitagóricos. No Home de Vitruvio, Leonardo expresou as ideas do arquitecto romano Marco Vitruvio, mostrando a figura masculina centrándoa nun círculo e nun cadrado.

Xa no s. XV, a perspectiva curvilínea atopou camiño nas pinturas de artistas interesados ​​nas distorsións da imaxe. O Retrato do matrimonio Arnolfini , pintado por Jan van Eyck en 1434, contén un espello convexo con reflexos das persoas na escena, mentres que o pintor Parmigianino, no seu Autorretrato nun espello convexo (1524), mostra a cara case sen distorsión do artista no centro, cun fondo moi curvado e a man do artista ao redor do bordo.

O espazo tridimensional pode representarse de maneira convincente na arte, como no debuxo técnico, por medios distintos á perspectiva. Os sistemas de proxección oblicua, incluída a perspectiva cabaleira (utilizada por artistas militares franceses para representar fortificacións no século XVIII), foron utilizados de forma continua por artistas chineses desde o primeiro ou segundo século até o século XVIII. Os chineses adquiriron a técnica da India, que a adquiriu da Antiga Roma. A proxección oblicua tamén aparece na arte xaponesa, como nas pinturas Ukiyo-e de Torii Kiyonaga (1752–1815).

• 
  Gravado de Luca Pacioli de De divina proportione (1509) cun triángulo equilátero sobre un rostro humano.
• 
  Cámara lúcida en uso. Scientific American, 1879.
• 
  Ilustración dun artista utilizando unha cámara escura. Século XVII.
• 
  Proporción: O Home de Vitruvio de Leonardo, c. 1490.
• 
  Teoría da perspectiva de Filippo Brunelleschi: la Trinità de Masaccio, c. 1426–1428, na Basílica de Santa María Novella.
• 
  Diagrama de Leon Battista Alberti da súa obra De pictura (1435), con piares en perspectiva sobre unha cuadrícula.
• 
  Perspectiva de Piero della Francesca na Flaxelación de Cristo, c. 1455–1460.
• 
  Perspectiva curvilínea: Espello curvo no Retrato de Giovanni Arnolfini e a súa dona de Jan van Eyck, 1434
• 
  Parmigianino, Autorretrato nun espello convexo, c. 1523–1524
• 
  Pitágoras cunha táboa de proporcións, na Escola de Atenas de Rafael Sanzio, 1509.
• 
  Proxección oblicua: Entrada e patio dun iamen. Detalle do rolo sobre a cidade de Suzhou, obra de Xu Yang encargada polo emperador Qianlong. Século XVIII.
• 
  Proxección oblicua: mulleres xogando shōgi, go e ban-sugoroku. Pintura de Torii Kiyonaga, Xapón, c. 1780.

Proporción áurea

O número áureo (aproximadamente igual a 1.618) xa era coñecido por Euclides. A proporción áurea foi reivindicada de forma persistente en tempos modernos pola súa presunta utilización na arte e especialmente na arquitectura do antigo Exipto, Grecia e outras culturas sen evidencias fiables.

Esta situación pode derivar en parte da confusión da "relación áurea" coa "medida dourada" ou "regra de ouro", que para os antigos gregos significaba "evitar o exceso en calquera dirección", non unha relación xeométrica. Desde o século XIX, moitos expertos e afeccionados á piramidoloxía argumentaron utilizando dubidosos razoamentos matemáticos para achar a proporción de ouro no deseño das pirámides, continuando a fantasía en filmes de historia-ficción. Afirmouse que no Partenón, un templo do século V a. C. en Atenas, utilízase a proporción áurea na súa fachada e no seu plano de planta, pero estas afirmacións tamén son refutadas polas medidas do monumento.

Da Gran Mesquita de Kairuán en Tunes tamén se afirmou que utilizou a proporción áurea no seu deseño, pero a citada proporción non aparece nas partes orixinais da mesquita. O historiador da arquitectura Frederik Macody Lund argumentou en 1919 que a Catedral de Chartres (século XIII), a Catedral de Laon (1157-1205) e a de Notre Dáme (París) (1160) están deseñadas de acordo co número áureo, debuxando liñas auxiliares para mostrar a súa tese. Outros estudosos argumentan que até o traballo de Pacioli en 1509, a proporción de ouro era descoñecida para os artistas e arquitectos. Por exemplo, a altura e o ancho da parte dianteira de Notre-Dáme de Laon teñen a proporción 8/5 ou 1.6, non 1.618. Tales termos da sucesión de Fibonacci convértense rapidamente en difíciles de distinguir da proporción áurea. Despois de Pacioli, a proporción áurea é máis perceptible nas obras de arte, incluída A Gioconda de Leonardo.

Outro número morfolóxico do que se escribiu profusamente é o número plástico, ideado en 1928 polo arquitecto holandés Hans van der Laan (orixinalmente en francés "noméelle radiant", o número radiante). O seu valor é a solución da ecuación cúbica

$x^{3}=x+1\,$

un número irracional, aproximadamente 1.325. Segundo o arquitecto Richard Padovan, está conectado coas fraccións características 3/4 e 1/7, que gobernan os límites da percepción humana ao relacionar un tamaño físico con outro. Van der Laan usou estas proporcións ao deseñar a igrexa de St. Benedictusberg Abbey (1967) nos Países Baixos.

[1]	[2]	[3]	[4]
[1] O cociente Base:Hipotenusa (b:a) da Gran Pirámide de Guiza, relacionouse con: 1:φ (Triángulo de Kepler), 3:5 (Triángulo 3-4-5), ou 1:4/π [2] Supostas liñas de proporción: Catedral de Laon [3] Rectángulos áureos superpuestos sobre A Gioconda [4] A igrexa da St. Benedictusberg Abbey (1967), obra de Hans van der Laan, utiliza nas súas proporcións o número plástico

Simetrías planas

Véxase tamén: Simetría, Grupo do papel pintado, Patróns xeométricos islámicos e Kilim.

Alfombra con dobre medallón. Anatolia Central (Konya-Karapınar), paso do século XVI ao XVII. Mesquita Alâeddin

As simetrías no plano utilizáronse durante milenios en obras téxtiles como alfombras, celosías e todo tipo de adornos.

Moitas alfombras tradicionais divídense nun campo central e un bordo de encadramento. Ambos poden presentar simetrías, aínda que nas tecidas a man a miúdo están lixeiramente alteradas por detalles, variacións de patrón e cambios de cor introducidos polo tecedor. Nos kilims de Anatolia os motivos utilizados son xeralmente simétricos. No deseño xeral adoita estar presente a simetría, con franxas ou arranxos agrupados de motivos aproximadamente hexagonais. O campo acostuma presentarse como un fondo asimilable a un patrón do grupo do papel pintado de configuración pmm, mentres o bordo toma a forma dun friso do tipo pm11, pmm2 ou pma2. Os kilims turcos e de Asia central a miúdo teñen tres ou máis fronteiras entre diferentes grupos de frisos. É obvio que os tecedores certamente buscaban a simetría, sen o coñecemento explícito das súas matemáticas.

O matemático e teórico da arquitectura Nikos Salingaros suxire que a "poderosa presenza" (efecto estético) dunha "grande alfombra", como as mellores alfombras de dous medallóns Konya do século XVII, créanse mediante técnicas matemáticas relacionadas coas teorías do arquitecto Christopher Alexander. Estas técnicas inclúen introducir zonas de cor como pares opostos; diferenciar áreas xeometricamente, ben utilizando formas complementarias ou equilibrando as direccións dos ángulos agudos; utilizar a complexidade a pequena escala (desde o nivel de nó cara a arriba) e a simetría a pequena e a grande escala; e a utilización de elementos repetidos nunha xerarquía de diferentes escalas (cunha relación de aproximadamente 2.7 de cada nivel ao seguinte). Salingaros sostén que "todas as alfombras consideradas artísticas satisfán polo menos nove das dez regras anteriores", e suxire que podería ser posible crear unha métrica a partir delas.

Na India atópanse os denominados jali, tallados en mármore para adornar tumbas e palacios. As celosías chinesas existen en 14 dos 17 grupos de simetría planar; a miúdo presentan simetría de espello, de dobre espello ou rotacional. Algunhas presentan un medallón central e outras inclúen un bordo cun friso. Moitas celosías chinesas foron analizadas matematicamente por Daniel S. Dye, que identificou Sichuan como o centro desta arte.

Dovelas girih

As simetrías teñen un papel moi destacado nas artes téxtiles, incluíndo o punto, os encaixes, os bordados e os distintos tipos de tecer, onde estes patróns poden ser decorativos ou indicar o status do propietario.

Os artigos de bordado e encaixe como manteis e tapetes de mesa, feitos con bobinas ou con paus ou renda de bilros tradicionais en Europa, desde Hungría a Camariñas en Galicia, poden ter unha ampla variedade de reflexións e rotacións simétricas, que foron exploradas matematicamente. Tamén se atopan simetrías nos entrelazados medievais, en todo tipo de obxectos.

A simetría rotacional atópase en estruturas circulares tales como cúpulas, en ocasións moi decoradas con patróns simétricos por dentro e por fóra, como na mesquita do xeque Lotf Allah de Isfahán (1619).

Na arte islámica, os patróns xeométricos están presentes en moitas formas de arte, especialmente nos embaldosados. Estes teselados fórmanse utilizando un conxunto de cinco formas de baldosas, a saber: un decágono regular, un hexágono alargado, unha paxarela, un rombo e un pentágono regular. Todos os lados destes azulexos teñen a mesma lonxitude; e todos os seus ángulos son múltiplos de 36° (π/5 radiáns), mostrando simetrías de cinco e dez módulos. As baldosas están decoradas con liñas de lacería en relevo (girih), xeralmente máis visibles que os límites das baldosas. En 2007, os físicos Peter Lu e Paul Steinhardt argumentaron que o lousado girih era similar ao cuasicristal definido pola teselación de Penrose. As baldosas xeométricas elaboradas con pequenas teselas (zellige) son un elemento distintivo na arquitectura de Marrocos.

As bóvedas decoradas con mocárabe (almocárabe ou muqarna) son tridimensionais, pero están deseñadas en dúas dimensións con debuxos de celas xeométricas.

Tamén se atopan interesantes patróns matemáticos nos estucos da arquitectura hispanomusulmá e en igrexas cristiás de todos os estilos, desde grandes obras a pequenas igrexas como a de St. Florian Wiedenzhausen de Baviera.

• 
  Detalle dun kilim de Hotamis, Anatolia central, comezo do século XIX.
• 
  Detalle dun brocado da dinastía Ming, utilizando un patrón cun teselado hexagonal.
• 
  Celosía Jali de mármore na tumba de Salim Chishti, Fatehpur Sikri, India.
• 
  Simetrías: bargello florentino.
• 
  Teito da mesquita do xeque Lotf Allah, Isfahán, 1619.
• 
  Simetría rotacional nun encaixe.
• 
  Teselado girih: patróns a escalas grandes e pequenas nunha enxunta do santuario de Darb-i Imam, Isfahan, 1453.
• 
  Teselados: mosaicos zellige na Madrasa de Bou Inania, Fez (Marrocos).
• 
  A complexa xeometría e os teitos da bóveda de almocárabe da mesquita Sheikh Lotfollah, Isfahán
• 
  Plano do arquitecto de unha quinta bóveda de muqarnas. Tira do Topkapı
• 
  Túpac Yupanqui; túnica procedente do Perú, 1450-1540, un téxtil andino indicador de un alto rango
• 
  Detalle decorativo na madrasa de Sherdor. Samarcanda, Uzbekistán.

Poliedros

Retrato de Luca Pacioli disertando sobre poliedros (1495)

Os sólidos platónicos e outros poliedros son un tema recorrente na arte occidental. Atópanse, por exemplo, nun mosaico de mármore onde aparece un pequeno dodecaedro estrelado atribuído a Paolo Uccello e que forma parte do chan da Basílica de San Marcos en Venecia; nos diagramas de poliedros regulares de Leonardo da Vinci debuxados como ilustracións para o libro 1509 de Luca Pacioli De Divina Proportione; como un rombicuboctaedro de cristal no retrato de Pacioli de Jacopo de' Barbari, pintado en 1495; e no poliedro truncado (e varios outros obxectos matemáticos) que aparecen no gravado de Albrecht Dürer titulado Melancolía I. Dürer (1471-1528) foi un artista alemán do Renacemento, que fixo importantes contribucións ao estudo dos poliedros no seu libro de 1525, Underweysung der Messung (Educación sobre a medición), destinado ao ensino da perspectiva, a xeometría en arquitectura, os sólidos platónicos, e os polígonos regulares. Probablemente estivo influenciado polos traballos de Piero della Francesca e Luca Pacioli durante as súas viaxes a Italia. Mentres que os exemplos de perspectiva en Underweysung der Messung están pouco desenvolvidos e conteñen imprecisións, o texto contén unha discusión detallada sobre os poliedros. Dürer foi tamén o primeiro en introducir no texto a idea do desenvolvemento dun poliedro, incluíndo poliedros despregados para que fiquen planos para a súa impresión. Tamén publicou en 1528 outro libro influente sobre as proporcións do corpo humano, titulado "Vier Bücher von Menschlicher Proportion (Catro libros sobre a proporción humana)".

O coñecido gravado titulado Melancolía I, representa a un ser alado, sentado en actitude pensativa. A imaxe inclúe un cadrado máxico e un trapezoedro triangular truncado. Estes dous elementos, e o gravado en conxunto, foron obxecto de máis interpretacións modernas que case calquera outra obra comparable, incluíndo un libro de dous volumes de Peter-Klaus Schuster, e unha influente análise contida na monografía de Erwin Panofsky.

Outro famoso pintor que incluíu poliedros nalgunhas das súas pinturas é Salvador Dalí. No seu cadro titulado A Última Cea, Cristo e os seus discípulos están representados dentro dun dodecaedro xigante. Outra das súas obras, a Crucifixión (1954), mostra un hipercubo despregado, que fai alusión á perspectiva divina en catro dimensións.

Dimensións fractais

Un batik, tecido tradicional procedente de Surakarta, Xava, como este parang klithik con patrón de espadas, ten unha dimensión fractal de entre 1.2 e 1.5

Os deseños tradicionais de batik, tinguidos en Indonesia co procedemento de reserva con cera, combinan motivos figurativos (elementos florais e vexetais) con motivos abstractos e algo caóticos, incluída a imprecisión derivada da aplicación da reserva máis e a variación aleatoria introducida polas gretas da propia cera. Os deseños de batik teñen unha dimensión fractal de entre 1 e 2, que varía en diferentes estilos rexionais. Por exemplo, o batik de Cirebon ten unha dimensión fractal de 1.1; os batiks de Yogyakarta e Surakarta no centro de Xava teñen unha dimensión fractal de 1.2 a 1.5; e os batiks de Lasem na costa norte de Xava e de Tasikmalaya en Xava occidental, teñen unha dimensión fractal de entre 1.5 e 1.7.

As obras de dripping do artista moderno Jackson Pollock son tamén distintivas pola súa dimensión fractal. A súa obra titulada Número 14, de 1948, ten unha dimensión de 1.45, mentres as súas pinturas posteriores tiveron dimensións fractais sucesivamente máis altas e, por conseguinte, patróns máis elaborados. Unha das súas últimas obras, Blue Poles, levoulle seis meses de traballo, e ten unha dimensión fractal de 1.72.

Unha relación complexa

O astrónomo Galileo Galilei na súa obra "O ensaiador" escribiu que "[O universo] está escrito na linguaxe das matemáticas, e os seus caracteres son triángulos, círculos e outras figuras xeométricas". Os artistas que se esforzan e buscan estudar a natureza, segundo Galileo, deben primeiro ver e entender completamente as matemáticas.

Con todo, os matemáticos trataron de interpretar e analizar a arte a través da lente da xeometría e da racionalidade. O matemático Felipe Cucker suxire que as matemáticas, e especialmente a xeometría, son unha fonte de regras para a "creación artística impulsada por regras", aínda que non a única. Algunhas das moitas cadeas da complexa relación resultante descríbense a continuación.

O matemático Godfrey Harold Hardy definiu un conxunto de criterios para cualificar a beleza matemática

As matemáticas como arte

Artigo principal: Beleza matemática.

O matemático Jerry P. King describe as matemáticas como unha arte, afirmando que "as claves das matemáticas son a beleza e a elegancia e non o aburrimento e os tecnicismos", e que a beleza é a forza motivadora da investigación matemática. King cita o ensaio publicado por Godfrey Harold Hardy en 1940, titulado Apoloxía dun matemático. Nel, Hardy analiza por que atopa dous teoremas da Antigüidade clásica como de primeira clase: a proba de Euclides de que hai infinitos números primos, e a proba de que a raíz cadrada de 2 é un número irracional. King avalía eses teoremas segundo os criterios de Hardy para estimar a elegancia matemática: "sobriedade, profundidade, xeneralidade, imprevisibilidade, inevitabilidade" e "economía" e describe a proba como "esteticamente agradable". O matemático húngaro Paul Erdős estivo de acordo en que as matemáticas posuían beleza, pero considerou as razóns máis aló da explicación: "Por que son fermosos os números? É como preguntar por que é fermosa a Novena Sinfonía de Beethoven. Si non ves o porqué, ninguén cho pode explicar. Eu sei que os números son fermosos".

Ferramentas matemáticas para a arte

Octopod, obra de Mikael Hvidtfeldt Christensen. Arte algorítmico producido co programa Structure Synth

As matemáticas aparecen no substrato de basicamente todas as artes: música, danza, pintura, arquitectura, escultura...

Cada unha está asociada coas matemáticas dun xeito particular. Grazas á súa conexión coas artes visuais, as matemáticas poden proporcionar ferramentas para os artistas, como as regras da perspectiva descritas por Brook Taylor e Johann Heinrich Lambert, ou os métodos de xeometría descritiva, posteriormente aplicados á modelaxe de sólidos por computador, e cuxos orixes teóricos se remontan a Dürer e a Gaspard Monge.

Artistas da Idade Media e do Renacemento (como Pacioli, Leonardo e Dürer) empregaron e desenvolveron ideas matemáticas ao investigaren formas novas de realizaren o seu traballo artístico. O uso da perspectiva comezou, malia algúns incipientes intentos de arquitectura grega antiga, con pintores italianos como Giotto no século XIII; regras como a do punto de fuga foron formuladas por Brunelleschi ao redor de 1413, e as súas teorías influíron definitivamente en Leonardo e Dürer.

O traballo de Newton sobre o espectro óptico influíu na teoría das cores de Goethe e, á súa vez, en artistas como Philipp Otto Runge, J. M. W. Turner, os membros da Irmandade Prerrafaelita, os puntillistas, os impresionistas, sobre Kandinski etc.

Os artistas tamén analizan a simetría dunha escena, e traballan sobre ese concepto. As mesmas ferramentas poden ser aplicadas por matemáticos que están a explorar a arte, ou por artistas inspirados nas matemáticas, como M. C. Escher ou o arquitecto Frank Gehry, quen argumentou que o deseño asistido por computadora lle permitiu expresarse dunha maneira completamente nova.

O artista Richard Wright argumenta que os obxectos matemáticos que poden construírse poden verse "como procesos para simular fenómenos" ou como obras de "arte computacional". Considera a natureza do pensamento matemático, observando que os matemáticos coñecían os fractais desde un século antes de que fosen recoñecidos como tales. Wright conclúe afirmando que é apropiado someter os obxectos matemáticos a calquera método utilizado para "chegar a un acordo con conceptos culturais como a arte, a tensión entre obxectividade e subxectividade, os seus significados metafóricos e o carácter dos sistemas de representación". Dá como exemplos unha imaxe do conxunto de Mandelbrot, outra xerada por un algoritmo de autómata celular e unha imaxe renderizada, e discute, con referencia ao Test de Turing, se os produtos dun algoritmo poden ser arte. Sasho Kalajdzievski, na súa obra "Math and Art: An Introduction to Visual Mathematics (Matemáticas e Arte: unha introdución ás matemáticas visuais) adopta un enfoque similar, analizando temas matemáticos visuais adecuados, como teselados, fractais e xeometría hiperbólica.

Algunhas das primeiras obras de arte computacional foron creadas por "Drawing Machine 1", un sistema ideado por Desmond Paul Henry, que consistía nunha computadora analóxica baseada nun visor de bombardeiro, exhibida en 1962. A máquina era capaz de crear debuxos lineais complexos, abstractos, asimétricos ou curvilíneos, pero repetitivos. Máis recentemente, Hamid Naderi Yeganeh creou formas suxestivas de obxectos do mundo real, como peixes e aves, usando fórmulas que son sucesivamente variadas para debuxar familias de curvas ou liñas en ángulo. Artistas como Mikael Hvidtfeldt Christensen crean obras de arte algorítmico escribindo rutinas para un sistema de software como Structure Synth: o artista dirixe o sistema para aplicar unha combinación desexada de operacións matemáticas a un conxunto de datos previamente elixido.

• 
  Escultura matemática, obra de Bathsheba Grossman, 2007
• 
  Escultura fractal: 3D Fraktal 03/H/dd, obra de Hartmut Skerbisch, 2003
• 
  Fibonacci word: detalle do traballo de Samuel Monnier, 2009
• 
  Imaxe de arte computacional producida por Desmond Paul Henry co seu "Drawing Machine 1", exhibido en 1962
• 
  A Bird in Flight, por Hamid Naderi Yeganeh, 2016, construído cunha familia de curvas matemáticas
• 
  Imaxe modificada mediante o programa Deep Dream

Das matemáticas á arte

Véxase tamén: Protocubismo, Teselación, M. C. Escher e Origami.

Theo van Doesburg: Seis Momentos no Desenvolvemento do Plano ao Espazo, 1926 ou 1929

O matemático e físico Henri Poincaré, autor de Ciencias e Hipóteses, foi lido amplamente polos cubistas, incluíndo a Pablo Picasso e a Jean Metzinger. Poincaré vía a xeometría euclidiana como unha das moitas configuracións posibles do espazo, non como unha verdade obxectiva absoluta. Picasso, na súa obra de 1907 As señoritas d'Avinyó explorou a proxección nunha cuarta dimensión para tratar de mostrar simultaneamente as figuras de fronte e de perfil.

A posible existencia dunha cuarta dimensión inspirou aos artistas a posibilidade de cuestionar a perspectiva clásica herdada do Renacemento: a xeometría non euclidiana converteuse noutra alternativa válida. O concepto de que a pintura se podería expresar matematicamente, en cor e forma, contribuíu ao cubismo, o movemento artístico que conduciu á arte abstracta. Metzinger, en 1910, escribiu que "[Picasso] presenta unha perspectiva móbil e gratuíta, desde a que ese enxeñoso matemático, Maurice Princet, deduciu toda unha xeometría".

O impulso de facer modelos de ensino ou investigación de formas matemáticas crea naturalmente obxectos que teñen simetrías e formas sorprendentes ou agradábeis. Algúns destes obxectos inspiraron a artistas como os dadaistas Man Ray Marcel Duchamp e Max Ernst, e tras Man Ray, a Hiroshi Sugimoto.

Retrato de Joella. Man Ray e Salvador Dalí (Museo Raíña Sofía)

Man Ray fotografou algúns dos modelos matemáticos conservados no Institut Henri Poincaré en París, incluíndo "Objet Matemathique" (Obxecto Matemático). Sinalou que representaba superficies de Enneper con curvatura constante, derivadas dunha pseudoesfera. Este fundamento matemático era importante para el, xa que lle permitía negar que o obxecto era "abstracto", permitíndolle afirmar que era tan real como o A Fonte (o urinal que Duchamp 'converteu' nunha obra de arte). Admitiu que a fórmula da superficie de Enneper que definía o obxecto "non significaba nada para min, pero as formas en si mesmas eran tan variadas e auténticas como calquera outra na natureza". Utilizou as fotografías dos modelos matemáticos como figuras da súa serie sobre as obras de Shakespeare, como a súa pintura "Antony and Cleopatra" de 1934. O reporteiro de arte Jonathan Keats, nun artigo da revista "ForbesLife", sostén que Man Ray fotografou "os paraboloides elípticos e os puntos cónicos coa mesma luz sensual que as súas imaxes de Alice Prin", e "reformula enxeñosamente os cálculos xeniais das matemáticas para revelar a topoloxía do desexo". Escultores do século XX como Henry Moore, Barbara Hepworth e Naum Gabo tamén tomaron inspiración dos modelos matemáticos. Moore escribiu sobre a súa Nai e fillo con cordas de 1938: "Sen dúbida, a fonte das miñas figuras con cordas foi o Museo de Ciencias de Londres ... Fascináronme os modelos matemáticos que vin alí ... "non foi o estudo científico destes modelos, senón a capacidade de mirar a través das cordas como nunha gaiola de paxaros e de ver unha forma dentro doutra, o que me emocionou".

Os artistas Theo van Doesburg e Piet Mondrian fundaron o movemento De Stijl, que pretendía "establecer un vocabulario visual de formas xeométricas elementais comprensibles por todos e adaptables a calquera disciplina". Moitas das súas obras de arte consisten visiblemente en cadrados e triángulos, ás veces tamén círculos. Os artistas de De Stijl traballaron en pintura, mobiliario e arquitectura. Logo da separación de De Stijl, Van Doesburg fundou o movemento de vangarda Art Concret, describindo a súa obra de finais dos 1920 titulada Seis Momentos no Desenvolvemento do Plano ao Espazo, como unha serie de cadrados negros sobre a diagonal dun fondo cadrado, como "unha estrutura que se pode controlar, unha superficie definida sen elementos aleatorios nin capricho individual", porén "Non lle falta espírito, non lle falta o universal e non lle falta... baleiro, xa que posúe un todo que se axusta ao ritmo interno". A crítica Gladys Fabre observou que hai dúas progresións traballando na pintura, os cadrados negros en crecemento e os fondos alternos.

As matemáticas do teselado, os poliedros, a configuración do espazo e a autorreferencia proporcionaron ao artista gráfico M. C. Escher (1898-1972) moito material para os seus gravados en madeira. No Bosquexo da Alhambra demostrou que se pode crear arte con polígonos e formas regulares como triángulos, cadrados ou hexágonos. Tamén usou polígonos irregulares para teselar o plano e a miúdo usou reflexións e translacións para patróns adicionais. Moitas das súas obras conteñen construcións imposibles, con obxectos xeométricos que configuran unha contradición entre a proxección en perspectiva e as tres dimensións, pero son agradables á vista humana. O seu gravado "Ascendente e Descendente" baséase na "escaleira imposible" creada polo científico Lionel Sharples Penrose e o seu fillo o matemático Roger Penrose.

Algúns dos moitos debuxos de teselado de Escher inspiráronse en conversas co matemático Harold Scott MacDonald Coxeter sobre a xeometría hiperbólica. Escher estaba especialmente interesado en cinco poliedros que aparecen moitas veces no seu traballo. Os sólidos platónicos (tetraedros, cubos, octaedros, dodecaedros e icosaedros) aparecen especialmente destacados en "Orde e Caos" e "Catro Sólidos Regulares". Estas figuras adoitan situarse dentro doutras formas que distorcen aínda máis o ángulo de visión e a conformación dos poliedros, proporcionando unha obra de arte en perspectiva multi-facética.

A complexidade visual das estruturas matemáticas, como as teselacións e os poliedros, inspirou unha gran variedade de obras de arte matemáticas. Stewart Coffin deseñou crebacabezas poliédricos en madeiras raras e fermosas; George W. Hart traballou na teoría de poliedros e esculpiu obxectos inspirados neles; Magnus Wenninger tamén realizou destacados modelos de poliedros estelados complexos.

As perspectivas distorsionadas con efectos de anamorfoses exploráronse na arte desde o s. XVI, cando Hans Holbein o Novo incorporou un cranio severamente distorto na súa pintura "Os embaixadores" de 1533. Moitos artistas desde aquela, incluído Escher, fixeron uso de trucos anamórficos.

As matemáticas propias da topoloxía inspiraron a varios artistas modernos. O escultor John Robinson (1935-2007) creou obras como Gordian Knot (no gordiano) e Bands of Friendship (Bandas de amizade), mostrando a teoría de nós en bronce puído.

Outros traballos de Robinson exploran a topoloxía de figuras toroidales. A súa obra Xénese baséase nun nó borromeo, un conxunto de tres aros entrelazados. O escultor Helaman Ferguson creou complexas superficies e outros obxectos topolóxicos. As súas obras son representacións de obxectos matemáticos; The Eightfold Way baséase no grupo lineal especial proxectivo PSL(2,7), un grupo finito de 168 elementos. A escultora Bathsheba Grossman baseou o seu traballo en estruturas matemáticas de maneira similar.

Un proxecto de investigación sobre artes liberais examina as conexións entre as matemáticas e a arte a través da banda de Möbius, flexágonos, origamis e fotografías panorámicas. No caso do origami, do que logo falaremos, podiamos considerar as aplicacións en eidos científicos e tecnolóxicos como a aeronáutica, e recentemente as investigacións de Robert Lang sobre os origamis descubriron axiomas que gobernan a súa creación, algúns coñecidos desde hai séculos e outros non. Mediante simulacións por ordenador Lang descubriu que se podía crear practicamente calquera figura complexa reducíndoa de forma matemática a un esquema, sendo logo o ordenador o que exploraría as fórmulas para indicar os pregues en papel que o artista tería de realizar.

Os obxectos matemáticos, incluídos o Atractor de Lorenz e o plano hiperbólico, creáronse utilizando a arte do tecido, coma o crochet. A tecedora estadounidense Ada Dietz escribiu unha monografía en 1949 titulada Algebraic Expressions in Handwoven Textiles ("Expresións alxebraicas en téxtiles tecidos a man"), que define patróns de tecido baseados ​​na expansión de polinomios de múltiples variables.

O matemático J. C. P. Miller usou o autómata celular Rule 90 para deseñar tapices que representaban tantas árbores como patróns abstractos de triángulos. Os "mathekniticians" Pat Ashforth e Steve Plummer usaron versións tecidas de obxectos matemáticos como flexágonos para as súas clases, aínda que a súa esponxa de Menger resultou ser demasiado complexa para tecerse e confeccionouse con lona plástica no seu lugar. O seu proxecto "mathghans" (Afghanos nas Escolas) introduciu o punto no currículo británico de matemática e tecnoloxía.

• 
  Anamorfismo: Os embaixadores, obra de Hans Holbein o Novo, 1533, cun cranio fortemente distorto.
• 
  Cuarta dimensión no cubismo: Esprit Jouffret, 1903. Tratado elemental de xeometría en catro dimensións.
• 
  Retrato de Pablo Ruiz Picasso, por Juan Gris. Proxección dun modelo tridimensional en facetas planas superpostas.
• 
  Movimento de De Stijl: Composition I (Still Life), obra de Theo van Doesburg de 1916.
• 
  Unha banda de Möbius, en forma de bufanda calcetada, 2007
• 
  Pedagoxía e arte: Magnus Wenninger con algúns dos seus poliedros estelados, 2009

Ilustrando matemáticas

Tríptico Stefaneschi de Giotto (1320), exemplo de recursión. Á dereita, detalle co Cardeal Stefaneschi suxeitando o tríptico completo

Fachada do Museo Magritte: o lenzo representa un escenario real envolvido polo propio lenzo

Autorretrato de M. C. Escher (1935) reflectido sobre unha esfera de cristal

A modelaxe está lonxe de ser a única maneira posible de ilustrar conceptos matemáticos. O Tríptico Stefaneschi de Giotto (1320), ilustra a recursividade na forma de mise en abyme. O panel central do tríptico contén no seu parte inferior esquerda a figura axeonllada do cardeal Stefaneschi, sostendo o tríptico completo como ofrenda. As pinturas metafísicas de Giorgio de Chirico, como o seu "Gran Interior metafísico" de 1917, exploran os niveis de representación na arte mediante a inclusión de pinturas dentro das súas pinturas.

A arte pode exemplificar paradoxos lóxicos, como as pinturas do surrealista René Magritte que se poden ler como bromas de semiótica sobre a confusión entre niveis de significado. En La condition humaine (1933), Magritte representa un cabalete (sobre o lenzo real), no que aparece unha vista a través dunha xanela que está enmarcada por cortinas "reais" na pintura. De maneira similar, Print Gallery de Escher (1956), representa unha cidade distorsionada que contén unha galería na que recursivamente aparece a propia imaxe, e así ad infinitum. Magritte fixo uso de esferas e cuboides para distorcer a realidade de forma diferente, pintándoas xunto a distintas casas na súa obra Aritmética mental de 1931 coma se fosen bloques de construción para nenos, pero do tamaño dunha casa. Un artigo de The Guardian sinalaba que a "imaxe misteriosa da cidade de xoguete" profetizaba a usurpación por parte do modernismo das "tradicionais formas acolledoras", pero que tamén xogaba coa tendencia humana a buscar patróns na natureza.

O cadro de Salvador Dalí, La cola de golondrina (1983), foi parte dunha serie inspirada na teoría das catástrofes de René Thom. O pintor e escultor español Pablo Palazuelo (1916-2007) centrouse na investigación da forma. Desenvolveu un estilo que describiu como a xeometría da vida e a xeometría de toda a natureza, consistente en formas xeométricas simples con patróns e cores detalladas, en obras como Angular I e Automnes, Palazuelo expresouse mediante transformacións xeométricas.

Adrian Gray ideou o equilibrio de rocas, xogando coas condicións de fricción e o centro de masas para crear composicións sorprendentes e aparentemente imposibles.

Os artistas, con todo, non necesariamente asumen literalmente as propiedades da xeometría como ciencia. Como Douglas Hofstadter escribiu na súa reflexión de 1980 sobre o pensamento humano, Gödel, Escher, Bach: un Eterno e Grácil Bucle, a través de (entre outras cousas) as matemáticas da arte: "A diferenza entre un debuxo de Escher e a xeometría non euclidiana é que nesta última, pódense atopar interpretacións comprensibles para os termos indefinidos, o que resulta nun sistema total comprensible, mentres que para o primeiro, o resultado final non se pode reconciliar coa propia concepción do mundo, sen importar canto se mire ás imaxes". Hofstadter discute a aparentemente paradoxal litografía "Print Gallery" de M. C. Escher, que representa unha cidade costeira que á vez contén unha galería de arte que parece conter outra pintura da cidade costeira, cun "bucle estraño ou xerarquía entramada" entre os distintos niveis de realidade da imaxe. O propio artista, observa Hofstadter, non se ve; a súa realidade e a súa relación coa litografía non son paradoxais. O baleiro central da imaxe tamén atraeu o interese dos matemáticos Bart de Smit e Hendrik Lenstra, que propoñen que podería conter unha copia de si mesma, rotada e encolleita mediante o efecto Droste; esta sería unha ilustración máis da recursividade alén do sinalado por Hofstadter.

Análise da historia da arte

A análise algorítmica de imaxes de obras de arte, por exemplo, usando fluorescencia de raios X, pode revelar información sobre a arte. Tales técnicas poden descubrir imaxes en capas de pintura cubertas máis tarde por un artista; axudar á historiadores da arte a visualizar unha obra de arte antes de que se grete ou se desvaneza; axudar a diferenciar unha copia dun orixinal, ou distinguir o estilo de pincelada dun mestre do dos seus aprendices.

Max Ernst experimentou con curvas de Lissajous na década de 1940.

O estilo denominado dripping ("goteo") ideado por Pollock posúe unha dimensión fractal definida; entre os artistas que poden influír no caos controlado, Max Ernst pintou curvas de Lissajous directamente facendo balancearse un cubo de pintura furado colgado sobre un lenzo.

Neil Dodgson investigou se as pinturas de raias de Bridget Riley se podían caracterizar matematicamente, concluíndo que aínda que a distancia de separación podía "proporcionar algunha caracterización" e o concepto de entropía global funcionaba nalgunhas pinturas, a correlación obtida non era concluínte, porque os seus patróns eran irregulares. A análise da entropía local funcionou mellor, e correlacionouse ben coa descrición do crítico de arte Robert Kudielka.

A medida estética do matemático George David Birkhoff, de 1933, propón unha métrica cuantitativa da calidade estética dunha obra de arte. Non tenta medir as connotacións dunha obra, como o significado dunha pintura, senón que se limita aos "elementos de orde". Para iso, combina (como suma) cinco destes parámetros: se existe un eixo vertical de simetría; se hai equilibrio óptico; cantas simetrías rotativas ten; como é o fondo da figura; e se hai características insatisfactorias, como ter dous vértices demasiado xuntos. Esta métrica, O, toma un valor entre −3 e 7. A segunda métrica, C, ten en conta os elementos da figura, que para un polígono é o número de distintas rectas que conteñen polo menos un dos seus lados. A continuación, define a súa medida estética da beleza dun obxecto como "O/C". Isto pódese interpretar como un equilibrio entre o pracer de ver o obxecto dado e a cantidade de esforzo necesario para asimilalo. A proposta de Birkhoff foi criticada de varias maneiras, non só por tratar de reducir a beleza a unha fórmula, aínda que el sempre negou telo feito.

Os estímulos á investigación matemática

Véxase tamén: Xeometría proxectiva e Matemáticas do origami.

Origami matemático: Resorte en Acción, por Jeff Beynon, construído cun único rectángulo de papel.

Orixe remota da xeometría proxectiva: diagrama de Alberti mostrando un círculo en perspectiva visto como unha elipse. Della Pittura, 1435–6

A arte ten estimulado o desenvolvemento das matemáticas, como cando a teoría de Brunelleschi sobre a arquitectura e pintura supuxo o inicio dun ciclo de investigación que conduciu ao traballo de Brook Taylor e Johann Heinrich Lambert sobre os fundamentos matemáticos do debuxo en perspectiva, e, en última instancia, ás matemáticas da xeometría proxectiva de Girard Desargues e Jean-Victor Poncelet.

A arte xaponesa de encartado de papel, o origami, foi revisada matematicamente por Tomoko Fuse. Partindo de pezas de papel congruentes, como cadrados, analiza as operacións necesarias para convertelas en poliedros ou teselas. Esta técnica foi utilizada en 1893 por T. Sundara Rao nos seus "Exercicios xeométricos de encartado de papel" para demostracións xeométricas. As matemáticas do origami foron exploradas no teorema de Maekawa, o teorema de Kawasaki, e nos axiomas de Huzita–Hatori.

Ilusións ópticas e Op-art

Artigo principal: Op-art.

Ilusión da espiral de Fraser, nomeada así por Sir James Fraser, que a descubriu en 1908.

As ilusións ópticas como a espiral de Fraser demostran sorprendentemente as limitacións na percepción visual humana, creando o que o historiador da arte Ernst Gombrich chamou un "truco desconcertante". As liñas en branco e negro que parecen formar espirais son de feito concéntricas. O estilo das pinturas e os gráficos do movemento Op-art de mediados do século XX aproveitou tales efectos para crear a impresión de movemento e patróns de vibración ou escintileos, propios do traballo de artistas como Bridget Riley, Spyros Horemis, e Victor Vasarely. e explorado teoricamente nos ensaios de Rudolf Arnheim, que participou como crítico explicando os traballos dalgúns deles no filme "The responsive eye".

Outros artistas neste ámbito amplo son Robert Bosh, Olafur Eliasson, Alexander Calder, Messen-Jaschin, Frank Stella ou Ad Reinhardt.

Xeometría sacra

Véxase tamén: Xeometría sacra e Música e matemáticas.

Unha corrente da arte desde a Grecia antiga en diante ve a Deus como o creador xeómetra do mundo, e a xeometría do mundo, por tanto, como sacra. A crenza de que Deus creou o universo cun plan xeométrico ten orixes antigas. Plutarco atribuíu a crenza a Platón, escribindo "Platón dixo que Deus xeometriza continuamente" (Convivialium disputationum, liber 8,2). Esta imaxe influíu no pensamento occidental desde aquela. O concepto platónico derivou á súa vez dunha noción de harmonía pitagórica na música, onde as notas estaban situadas en espazos de proporcións perfectas, que se correspondían ás lonxitudes das cordas da lira; de feito, os pitagóricos sostiñan que todo estaba organizado polo Número. Da mesma forma, no pensamento platónico, os sólidos platónicos (o cinco poliedros regulares convexos) ditan as proporcións atopadas na natureza e na arte. Unha ilustración dun manuscrito medieval pode referirse a un verso do Antigo Testamento: "Cando estableceu os ceos, eu estaba alí: cando estableceu un compás sobre a face do profundo" (Proverbios 8:27), que mostra a Deus debuxando o universo cun par de compases.

En 1596, o astrónomo e matemático Johannes Kepler modelou o universo como un conxunto de sólidos platónicos aniñados, determinando os tamaños relativos das órbitas dos planetas. Dúas pinturas de William Blake, Ancient of Days e Isaac Newton, tentan representar o contraste entre o mundo espiritual matematicamente perfecto e o mundo físico imperfecto. Dalí, pola súa banda, na súa obra de 1954 Crucifixión, visualiza a cruz como un hipercubo, que representa a perspectiva divina con catro dimensións en lugar das tres habituais. Noutra das súas obras, A Última Cea (1955), Cristo e os seus discípulos están representados no interior dun gran dodecaedro xigante

• 
  Deus o xeómetra. Codex Vindobonensis, c. 1220
• 
  Sólidos platónicos encaixados, modelo dos planetas no sistema solar incluído no Mysterium Cosmographicum de Johannes Kepler, 1596
• 
  The Ancient of Days, obra de William Blake, 1794
• 
  Newton, no lugar de Deus como xeómetra, de Blake, c. 1800
• 
  Asociación de Deus cunha forma triangular (reverso dun billete de 1 dólar estadounidense).
• 
  Símbolos masónicos: Deus como o supremo arquitecto.

Véxase tamén

Bibliografía

• Cucker, Felix (2013). Manifold Mirrors: The Crossing Paths of the Arts and Mathematics (en inglés). Cambridge / Nova York: Cambridge University Press. ISBN 978-0-521-72876-8. 
• Gamwell, Lynn (2015). Mathematics and Art: A Cultural History (en inglés). Princeton: Princeton University Press. ISBN 978-0-691-16528-8. 
• King, Jerry P. (1992). The Art of Mathematics (en inglés). Nova York: Fawcett Columbine. ISBN 978-0-449-90835-8. 
• Miller, Arthur I. (2001). Einstein, Picasso: Space, Time, and the Beauty That Causes Havoc (en inglés). Nova York: Basic Books. ISBN 978-0-465-01860-4. 

Ligazóns externas

• Bridges Organization conferencia sobre conexións entre arte e matemáticas
• Bridging the Gap entre Math and Art - Presentación de diapositivas de Scientific American
• Conexións no espazo: topoloxía na arte
• Descubrindo a arte das matemáticas
• Matemáticas e Arte - AMS
• Mathematics and Art - Alexander Bogomolny
• Imaxes matemáticas - American Mathematical Society
• Matemáticas en Arte e Arquitectura - Universidade Nacional de Singapura
• Mathematical Art - Museo Virtual de Matemáticas
• Cando a arte e as matemáticas chocan - Science News
• Por que a historia das matemáticas é tamén a historia da arte: Lynn Gamwell en The Guardian