Factorización
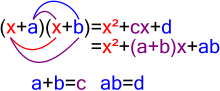
En matemáticas, a factorización consiste en escribir un número ou outro obxecto matemático como produto de varios factores, normalmente obxectos máis pequenos ou máis sinxelos do mesmo tipo. Por exemplo, 3 × 5 é un factorización do enteiro 15, e (x – 2)(x + 2) é un factorización do polinomio x2 – 4.
A factorización non se adoita a considerar en tanto a estar a traballar dentro de sistemas de número que posúen división, como os números reais ou complexos, xa que calquera pode ser trivialmente escrito como se non é cero ou unha unidade. Con todo, pódense obter factorizacións que teñan un significado claro, por exemplo se se escribe un número racional ou unha función racional en termos máis pequenos e separando os factores do numerador e o denominador.
Nas matemáticas da Antiga Grecia, a factorización soamente se consideraba no caso dos enteiros. Daquela probouse o teorema fundamental da aritmética, que afirma que todos os enteiros positivos poden ser descompostos nun produto de números primos, que non poden ser factorizados en enteiros maiores ca 1. Ademais, esta factorización é única a menos de cambios da orde dos factores. Malia que a factorización de enteiros case semella o contrario á multiplicación, é moito máis difícil algoritmicamente e neste feito baséase o sistema criptográfico RSA para pór en funcionamento unha criptografía de chave pública.
A factorización de polinomios tamén foi estudada ao longo dos séculos. En álxebra xeral, factorizar un polinomio é reducir o problema de atopar as súas raíces a atopar as raíces dos factores. No caso dos polinomios con coeficientes enteiros ou pertencentes a un corpo, estes posúen a propiedade da factorización única, unha versión do teorema fundamental da aritmética na que os polinomios irredutíbeis substituíron os números primos. En particular, un polinomio dunha variable cos coeficientes complexos admite unha única (sen ter en conta a orde) factorización en polinomios lineares: isto é unha versión do teorema fundamental da álxebra. Neste caso, a factorización pode ser feita cos algoritmos de atopar raíces.
Un anel conmutativo posúe a propiedade de factorización única é chamada dominio de factorización única. Malia de existir aneis de enteiros alxébrico que non son dominios de factorización única, estes satisfán a propiedade máis débil dominios de Dedekind: factorización única de ideais en ideais primos.
O termo factorización tamén fai referencia a descomposicións máis xerais dun obxecto matemático no produto de obxectos máis pequenos ou máis sinxelos. Por exemplo, cada función pode ser factorizada como unha composición dunha función sobrexectiva cunha función inxectiva. As matrices posúen moitas clases de factorizacións. Por exemplo, cada matriz ten unha única factorización LUP como produto dunha matriz triangular inferior L, con tódalas entradas diagonais iguais a un, unha matriz triangular superior U, e unha matriz permutación P, e esta é unha formulación de matriz de eliminación de Gauss.
Enteiros[editar | editar a fonte]
Polo teorema fundamental da aritmética, todo enteiro maior que 1 ten unha única (a menos cambios da orde) factorización en números primos, que son os enteiros que non poden ser factorizados no produto de enteiros maiores que 1.
Para calcular a factorización dun enteiro n, precísase dun algoritmo para atopar un divisor q de n ou que n é primo, e polo tanto non existe q. De atoparen o divisor q, obteríanse dous factores de n, n / q e q, nos que, ao aplicárenlles este algoritmo repetidamente, conséguese a factorización completa de n.[1]
Para atopar un divisor q de n, se ten algún, abonda con probar todos os valores q tal que 1 < q e q2 ≤ n. Chega con probar só con estes porque se r é un divisor de n tal que r2 > n , entón q = n / r é un divisor de n tal que q2 ≤ n, e xa tería sido atopado
Ao procurárense divisores en orde crecente, o primeiro divisor que sexa atopado ten que ser necesariamente un número primo, e o cofactor r = n / q non pode ter ningún divisor menor que q. Para conseguiren a factorización completo, abondará con continuar o algoritmo na procura dun divisor de r que nin é máis pequeno que q, nin é máis grande que √r.
Non é preciso probar tódolos valores de q para aplicar o método, pois chega con probar con todos os primos divisores. Mais isto xa precisa dunha táboa de números primos como, por exemplo, a xerada mediante a criba de Eratóstenes. Como método de factorización fai esencialmente o mesmo traballo como a criba de Eratosthenes, en xeral é máis eficiente de probar como divisor só aqueles números que non é evidente se son primos ou non. Tipicamente, procedendo por probar con 2, 3, 5, e os números maiores a 5, co último díxito é 1, 3, 7, 9 e coa suma dos díxitos non múltiplo de 3.
Este método funciona ben para a factorización de números enteiros pequenos, mais é ineficiente para máis grande enteiros. Por exemplo, Pierre de Fermat non foi quen de descubrir que o sexto número de Fermat
non é un número primo. De feito, a aplicación do método anterior precisaría máis que 10 000 divisións, ao ter o número 10 díxitos decimais.
Na actualidade coñécense algoritmos de factorización máis eficientes, mais fican relativamente ineficientes ao tentar factorizar un número de 500 díxitos, que é o produto de dous primos escollidos ao chou, incluso cos ordenadores máis potentes. Isto é o que asegura a seguranza do sistema criptográfico RSA, que é amplamente utilizado para comunicación segura en Internet.
Exemplo[editar | editar a fonte]
Farase un exemplo da factorización de n = 1386 en primos:
- Comézase dividindo por 2: o número é par, e n = 2 · 693. Continúase con 693, e 2 como primeiro divisor candidato.
- 693 é impar (2 non é divisor), mais é un múltiplo de 3: 693 = 3 · 231 e n = 2 · 3 · 231. Continúase con 231, e 3 como primeiro divisor candidato.
- 231 = 3 · 77 , e é tamén un múltiplo de 3: un ten n = 2 · 32 · 77 , por isto n = 2 · 32 · 77. Continúase con 77, e 3 como primeiro divisor candidato.
- 77 non é un múltiplo de 3 porque a suma dos seus díxitos é 14, que non un múltiplo de 3. Tampouco é un múltiplo de 5, ao non ser o seu último díxito é 7. O próximo divisor a probaren é 7. Temos que 77 = 7 · 11, e entón n = 2 · 32 · 7 · 11. Isto amosa que 7 é primo (cousa fácil de probar directamente). Continúase con 11, e 7 como primeiro divisor candidato.
- Como 72 > 11, remata; 11 é primo, e a factorización en primos é n = 2 · 32 · 7 · 11.
Expresións[editar | editar a fonte]
A manipulación de expresións está na base da álxebra, e a factorización é un dos métodos máis importantes. Por exemplo, ao poñer unha ecuación na forma factorizada E⋅F = 0, o resolución do problema divídese nos dous problemas independentes (a miúdo tamén máis sinxelos) E = 0 e F = 0. Cando unha unha expresión pode ser factorizado, os factores son a miúdo moito máis sinxelo e poden ofrecer unha mellor visión do problema. Por exemplo,
que ten 16 multiplicacións, 4 subtraccións e 3 adicións, pode ser factorizada á expresión
que só ten dúas multiplicacións e tres subtraccións. Ademais, a forma factorizada amosa con claridade as raíces x = a,b,c do polinomio en x representado por esta expresión.
Doutra banda, a factorización non é sempre posíbel, ou cando é posíbel, os factores non son sempre máis sinxelo. Por exemplo, pode ser factorizado en dous factores irredutíbeis: e .
A solución de ecuación alxébricas pode pensarse como un problema de factorización e, de feito, o teorema fundamental da álxebra pode ser enunciado cun carácter de factorización: todo polinomio x de grao n cos coeficientes complexos factoriza en n factores lineais para i = 1, ..., n, onde os ai son as raíces do polinomio.[2] Aínda que a estrutura da factorización é coñecida nestes casos, os ai xeralmente non se poden calcular en termos de radicais (raíces n-ésimas), polo teorema de Abel–Ruffini. Na maioría destes casos, o único que se pode facer calcular unha aproximación da raíz con algún algoritmo para encontrar raíz.
Historia da factorización de expresións[editar | editar a fonte]
O uso sistemático de manipulacións alxébricas para simplificar expresións (máis especificamente ecuacións) rexístrase até século IX, co libro Libro Compendio sobre Cálculo por Restauración e Balanceamento de Al-Khwarizmi, titulado con dous tipos de manipulación. Con todo, mesmo para solucionar ecuacións cadráticas, a factorización non se utilizou até a publicación en 1631 do traballo de Thomas Harriot, dez anos após a súa morte.[3]
No seu libro Artis Analyticae Praxis ad Aequationes Algebraicas Resolvendas, Harriot debuxou, nunha primeira sección, táboas para adición, subtracción, multiplicación e división de monomiais, binomiais, e trinomiais. Entón, nunha segunda sección, montou a ecuación aa − ba + ca = + bc , e mostrou que isto emparella a forma da multiplicación, xa proporcionada, sendo a factorización (a − b)(a + c) . [4]
Métodos xerais[editar | editar a fonte]
Os métodos que son descritos abaixo aplícanse a calquera expresión que é unha suma, ou ben pode ser transformado nunha suma. Por tanto, acotío son usadas cos polinomios, mesmo tamén se poden aplicar cando os termos da suma non son monomios, senón que son produto de variábeis e constantes.
Factor común[editar | editar a fonte]
No caso de seren produtos todos os termos dunha suma e que algúns factores sexan comúns a tódolos termos, pola propiedade distributiva pódese factorizar este factor común. Tamén, de haber coeficientes enteiros, pódese sacar fóra o máximo común divisor destes coeficientes.
Por exemplo,[5]
Xa que 2 é máximo común divisor de 6, 8, e 10, e divide tódolos termos.
Agrupación[editar | editar a fonte]
Ás veces, ao agruparen os termos faise posíbel aplicar outros métodos para factorizar. Por exemplo, para factorizar
pódese remarcar os dous primeiros termos comparten o factor común x e os dous últimos termos, o factor común y. Así
Entón, agora os dous termos actuais comparten o factor común x + 5, que leva á factorización
En xeral, isto funciona para sumas de 4 termos que foron obtidas como o produto de dous binomiais. A pesar de non ser frecuentemente, este método tamén se pode empregar para exemplos máis complicados.
Sumando e restando termos[editar | editar a fonte]
Ás veces, algunha agrupacións de termos deixa aparecer unha parte dun patrón recoñecíbel. Entón é útil de engadir termos para completar o patrón, e restarllos para non mudaren o valor da expresión.
Un uso típico disto é o método de "completar cadrados" para conseguir a fórmula de resolución de ecuación de segundo grao.
Outro exemplo é a factorización de , que un presenta a raíz cadrada imaxinaria de –1, xeralmente denotado como i, entón tense unha diferenza de termos
Con todo, pódese tamén querer unha factorización con coeficientes de números reais. Sumando e restando e agrupacndo tres termos xuntos, un pode recoñecer o termo dun binomial
Sumar e restar tamén acádase a factorización
Estas factorizacións non só traballan sobre os números complexos, mais tamén sobre calquera corpo onde 1, 2 ou –2 sexan cadrados. Nun corpo finito, o produto de dous termos non cadrados e un termo cadrado, isto implica que o polinomio , que é irredutíbel sobre o enteiros, é reducíbel modulo calquera número primo. Por exemplo
- xa que
- xa que
- xa que
Patróns recoñecíbeis[editar | editar a fonte]
Moitas identidades proporcionan igualdades entre unha suma e un produto. Os métodos anteriormente descritos poden ser utilizados para illar na expresión a parte da suma, para despois substituíla por un produto.
Nas seguintes identidades, o lado dereito será usado como patrón. Deste xeito, as variábeis E e F que aparecen na identidades poden representar calquera subexpresión da expresión a factorizar.[6]
- Diferenza de dous cadrados
- Por exemplo,
- Diferenza/de suma de dous cubos

- Diferenza de dúas potencias cuartas
- Diferenza/de suma de dúas potencias n-ésimas
- Nas identidades seguintes, ao factorizar aparecen termos máis longos:
- Diferenza, expoñente uniforme
- Diferenza, mesmo ou expoñente estraño
- Isto é un exemplo que amosa que un factor pode ter moitos máis termos que a suma que factoriza.
- Suma, expoñente estraño
- (Obtido por cambiante F por –F na fórmula anterior)
- Suma, expoñente uniforme
- Se o expoñente é unha potencia de dos, a expresión non se pode factorizar en xeral sen engadir números complexos (de conter E e F números complexos, pode mudar o caso). Se n te un divisor impar, que é n = pq con p impar, poderíase usar fórmula do caso de expoñente impar aplicado a
- Trinomiais e fórmulas cúbicas
- Expansións binomiais

- O teorema do binomial subministra patróns que facilmente poden ser recoñecido grazas aos enteiros que aparecen. Con graos pequenos:
- Máis xeralmente, os coeficientes das formas expandidas de e son os coeficientes binomiais que aparecen na n-ésima fileira do triángulo de Pascal.
Raíces de unidade[editar | editar a fonte]
As n-ésimas raíces da unidade son os números complexos tales que son a raíz do polinomio e son da forma:
para
Dedúcese para dúas expresións calquera E e F, tense:
Se E e F son expresión reais, de quereren factores reais, teríase que substituír cada par de complexos factores conxugados polo seu produto. Como o complexo conxugado é e dedúcese a seguinte real factorizacións (cambiando dun ao outro por trocando k en n – k ou n – k +1, e aplicando fórmulas trigonométricas:
O coseno que aparece nestas factorizacións é un número alxébrico, e pode ser expresado en termos de radicais (isto é posíbel porque o seu grupo de Galois é cíclico); con todo, estas expresións radicais son demasiado complicadas para ser utilizadas, excepto valores baixos de n. Por exemplo
A miúdo, quérese unha factorización con coeficientes racionais. Tal factorización implica polinomios ciclotómicos. Para expresar factorizacións racional de sumas e diferenzas ou potencias, precisamos da notación para a homoxeneización dun polinomio: se a súa homoxeneización é o polinomio bivariante
Entón, tense que
onde os produtos son fanse sobre tódolos divisores de n, ou tódolos divisores de 2n que non dividen n, e é o n-ésimo polinomio ciclotómico.
Por exemplo,
aa que o divisores de 6 son 1, 2, 3, 6, e o divisores de 12 que non divide a 6 son 4 e 12.
Polinomios[editar | editar a fonte]
Nos polinomios, a factorización vai fortemente ligada co problema de solucionar ecuacións alxébricas. Unha ecuación alxébrica ten a forma
onde
onde P(x) é un polinomio en x, tal que . A solución desta ecuación, ou raíz do polinomio, é un valor r de x tal que
Se
é unha factorización de P como produto de dous polinomios, entón as raíces de P son a unión das raíces de Q e mais as raíces de R. Así, solucionar P redúcese aos problemas, máis sinxelos, de solucionar Q e R.
Inversamente, o teorema do factor afirma que, se r é unha raíz de P, entón P pode ser escribir da forma
onde Q(x) é o cociente da división euclidiana de P por x – r.
Se os coeficientes de P son números reais ou complexos, o teorema fundamental da álxebra afirma que P ten unha raíz real ou complexa. Entón, utilizado co teorema do factor recursivamente, resulta en que
onde son as raíces, reais ou complexas, de P e con posíbeis repeticións. Esta factorización completa é única levada a orde dos factores.
De seren reais os coeficientes de P, polo xeral quérese tamén unha factorización onde os factores tivesen coeficientes reais. Neste caso, os factores da factorización completa poden chegar a ter grao dous. Este factorización pode ser facilmente deducida da forma factorización completa. De feito, se r = a + ib é unha raíz non real de P, entón o seu conxugado s = a - ib é tamén unha raíz de P, xa que
e entón
Polo que o produto
é un factor de P de só coeficientes reais. De continuaren a facer esta agrupación de factores non reais, chegase finalmente até conseguir unha factorización de factores reais que son polinomios de graos un ou dous.
Para calcular estas factorizacións reais ou complexas, tense que coñecer as raíces do polinomio, malia que, en xeral, non poderán ser calculadas exactamente, e ter que recorrer a valores aproximados dos valores das raíces.
A maioría de ecuacións alxébricas atopadas na práctica son de coeficientes enteiros ou racionais, e quererase unha expresión en factores da mesma clase. Neste caso, O teorema fundamental da aritmética xeneraliza en que os polinomios con coeficientes enteiro ou racionais teñen a propiedade de factorización única . Máis precisamente, todo polinomio cos coeficientes racionais factoriza nun produto
onde q é un número racional e son polinomios non constantes con coeficientes enteiro que son irredutíbeis e primitivos, isto é, que ningún pode escribirse como produto de dous polinomios (de coeficientes enteiros) que non son nin 1 nin –1 (os enteiros son considerados como polinomios de grao cero). Ademais, esta factorización é única ao non ter en conta a orde dos factores e a multiplicación por –1 dun número par de factores.
Malia da existencia de algoritmos eficientes para calcular esta factorización, desafortunadamente, para o cálculo a man son complicados de máis para ser usados. Ademais das heurísticas xerais xa descritas anteriormente, só hai uns cantos métodos dispoñíbeis neste caso, os cales xeralmente traballan só para polinomios de grao baixo e con poucos coeficientes non nulos. O principais métodos son descritos nas próximas subseccións.
Factorización primitiva baseada no contido[editar | editar a fonte]
Todo polinomio con coeficientes racionais, pode ser factorizado de xeito único como produto dun número racional e un polinomio de coeficientes enteiro, que é primitivo (o máximo común divisor dos coeficientes é 1) e o seu coeficiente principal (coeficiente do termo do grao máis alto) é positivo. Por exemplo:
Nesta factorización, ao número racional nomease o contido e ao polinomio primitivo, como a parte primitiva. O cálculo da factorización pode ser feita cos seguintes pasos:
- En primeiro lugar, redúcense tódolos coeficientes a un denominador común, para conseguiren o cociente dun polinomio con coeficientes enteiro por un enteiro q.
- Entón sácase como factor común a máximo común divisor p dos coeficientes deste polinomio para conseguir a parte primitiva, e sendo o contido
- Finalmente, se se precisa, múdanse os signos de p e de tódolos coeficientes da parte primitiva.
Esta factorización pode producir un resultado que é máis grande ca do polinomio orixinal (o exemplo típico é se hai moitos denominadores coprimos), mais, mesmo cando isto é o caso, a parte primitiva é xeralmente máis fácil de manipular para factorizacións posteriores.
Utilizando o teorema do factor[editar | editar a fonte]
- Artigo principal: Teorema do factor.
O teorema do factor expón que, se r é raíz dun polinomio
(o número que cumpre que P(r) = 0), entón hai un factorización
onde
con e para i = 1, ..., n – 1
Isto pode ser útil cando se coñece unha raíz do polinomio tanto dunha inspección ou dunha información externa. Para calcular Q(x), no canto de empregar a fórmula anterior, tamén é posíbel usar a regra de Ruffini.
Por exemplo, para o polinomio un facilmente podería ver que a suma dos seus coeficientes é 0. Por isto, r = 1 é unha raíz. Como r + 0 = 1, e tense que
Raíces racionais[editar | editar a fonte]
- Véxase tamén: Teorema das raíces racionais.
A procura das raíces racionais dun polinomio terá sentido só de traballaren con polinomios con coeficientes racionais. A factorización primitiva baseada no contido (xa vista) reduce o problema de buscar raíces racionais ao caso de polinomios con coeficientes enteiro tal que o máximo común divisor dos coeficientes é 1,
Se é unha raíz racional do polinomio
o teorema do factor di que ten unha factorización
onde ámbolos dous factores teñen coeficientes enteiro (que Q teña coeficientes enteiros vén da fórmula do cociente de P(x) por ).
Ao compararen coeficientes de grao n e os coeficientes constantes na igualdade de enriba, é claro que, se é unha raíz racional en forma reducida, entón q é divisor de p é un divisor de Por tanto, hai un número finito de posibilidades para p e q e poden ser exploradas de forma sistemática.[7]
Por exemplo, se o polinomio
ten unha raíz racional entón p ten que dividir a 6 e q a 2, por tanto e Ademais, se x < 0, tódolos termos do polinomio son negativos, implicando que non ten raíces reais negativas. De acordo a todo isto,
o cálculo directo amosa que é unha raíz e que non hai outra raíz racional. Aplicar o teorema do factor leva finalmente á factorización
Método AC[editar | editar a fonte]
Ao restrinxir só a polinomios cadráticos, este método pode ser adaptado na chamado método ac de factorización.[8]
Sexa o polinomio cadrático de coeficientes enteiro. Se ten unha raíz racional, o seu denominador ten que dividir a . Por tanto, de escribiren a raíz como fracción reducíbel , polas fórmulas de Vieta, a outra raíz é
Con Por isto a segunda raíz é tamén racional, e segundo a fórmula de Vieta tense que
isto é
Explorando tódolos pares de enteiros cuxo produto é ac consegue as raíces racionais, se é que existen.
Por exemplo, no caso do polinomio cadrático
A exploración dos factores de ac = 36 leva a 4 + 9 = 13 = b, obtendo as dúas raíces
e a factorización
Utilizando fórmulas para raíces de polinomios[editar | editar a fonte]
Todo polinomio cadrático dunha variábel factorizado utilizando a fórmula cadrática:
onde e son as dúas raíces do polinomio.
Se a, b, c son todos reais, os factores son reais se e só se o discriminante é non-negativo. De no ser deste xeito, o polinomio cadrático non factoriza con factores reais non constantes.
A fórmula cadrática é válida cando os coeficientes pertencen a calquera corpo de característica diferente de 2, e, en particular, para coeficientes nun corpo finito cun número impar de elementos.[9]
Tamén existen fórmulas para raíces polinomios de graos 3 e 4, mais son en xeral complicados de máis para uso práctico. O teorema de Abel–Ruffini demostra que non existen fórmulas xerais para as raíces en termos de radicais para polinomios de grao cinco ou maior.
Usando relacións entre raíces[editar | editar a fonte]
Pode ocorrer que un sabe algunha relación entre as raíces dun polinomio e os seus coeficientes. Utilizando este coñecemento pode axudar a factorizar o polinomio e atopando as súas raíces. A teoría de Galois está baseada nun estudo sistemático das relacións entre raíces e coeficientes, que inclúe as fórmulas de Vieta.
Aquí, considerarase o caso máis sinxelo onde dúas raíces e dun polinomio satisfán a relaciónonde Q é un polinomio.
Isto implica que é unha raíz común de e De aí que, polo tanto, tamén é unha raíz do máximo común divisor de ámbolos dous polinomios. Entón o máximo común divisor é un factor non constante de e o algoritmo de Euclides de polinomios permite calculalo
Por exemplo,[10] se se adiviña que ten dúas raíces que suman a cero, pódese aplicar entón o algoritmo de Euclides e O primeiro paso consiste en sumar e dando o resto de
Entón, dividindo por dá cero como novo resto, e x – 5 como cociente, chegando así á factorización completa
Dominios de factorización única[editar | editar a fonte]
O enteiros e o polinomios sobre un corpo comparte a propiedade de factorización única, que consiste en que todo elemento non nulo factoriza nun produto de elementos invertíbeis (unha unidade, ±1 no caso de enteiros) e un produto de elementos irredutíbel (números primos, no caso dos enteiros), e este factorización é única apenas cambios da orde dos factores. Os dominios de integridade que comparten esta propiedade é son chamados dominios de factorización única (DFU).
O máximo común divisor sempre existe nos DFU e, inversamente, todo dominio de integridade no que o máximo común divisor existe é un DFU. Todos os dominios de ideais principais son un DFU.
Un dominio euclideá é un dominio de integridade no cal está definida unha división euclidiana, similar a dos enteiros. Todo dominio euclidiano é un dominio de ideais principais e, polo tanto, un DFU.
Nun dominio euclidiano, a división euclidiana permite definir un algoritmo de Euclides para calcular o máximo común divisor. Con todo, isto non implica a existencia dun algoritmo de factorización
Ideais[editar | editar a fonte]
En teoría de números alxébricos, o estudo de ecuacións diofantianas guiou os matemáticos, durante o século XIX, até chegaren a introducir as xeneralizacións dos enteiros chamados enteiros alxébricos. Os primeiros aneis de enteiros alxébricos estudados teñen sido o anel que considera os enteiros gaussianos e o que considera os enteiros de Eisenstein. Estas dúas clases de enteiros alxébricos comparten cos enteiros tradicionais a propiedade de ser dominios de ideais principais, e ter así a propiedade de factorización única.
Desafortunadamente, axiña se demostrou que a maioría de aneis de enteiros alxébricos non son principais e non teñen factorización única. Deles, o exemplo máis sinxelo é en que
e todos estes factores son irredutíbeis.
A carencia de factorización única é unha gran dificultade para solucionar ecuacións diofantianas. Por exemplo, moitas probas incorrectas do Último Teorema de Fermat (probabelmente incluíndo a demostración de Fermat de "teño unha proba verdadeiramente marabillosa disto, mais esta marxe é demasiado estreita para contela") foron baseadas na suposición implícita dunha única factorización.
Dedekind resolveu esta dificultade, quen probou que os aneis de enteiros alxébricos teñen unha única factorización de ideais: nestes aneis, todo ideal é un produto de ideais primos, e esta factorización é única levado a orde dos factores. Os dominios de integridade que teñen esta propiedade de factorización única son chamados dominios de Dedekind. Teñen moitas propiedades agradábeis que lles fan fundamentais en teoría de número alxébricos.
Matrices[editar | editar a fonte]
- Artigo principal: Descomposición de matrices.
Os aneis de matrices son non conmutativos e non teñen unha única factorización: hai, en xeral, moitos xeitos de escribir unha matriz como produto de matrices. Así, o problema da factorización muda a consistir no problema de atopar factores de certas formas específicas. Por exemplo, a descomposición LU factoriza unha matriz como o produto dunha matriz triangular inferior e mais unha matriz triangular superior. Ás veces non é sempre posíbel, polo que se considera a "descomposición LUP" tendo unha matriz permutación como o terceiro factor.
Unha matriz lóxica representa un relación binaria, e multiplicación de matrices corresponde á composición de relacións. A descomposición dunha relación factorizándoa serve para percibir mellor a natureza da relación, como no caso dunha relación difuncional.
Notas[editar | editar a fonte]
- ↑ Hardy; Wright (1980). Oxford Science Publications, ed. An Introduction to the Theory of Numbers (5ª ed.). ISBN 978-0198531715.
- ↑ Klein 1925, pp. 101–102
- ↑ In Sanford, Vera (2008) [1930]. Read Books, ed. A Short History of Mathematics. ISBN 9781409727101..
- ↑ Harriot, Artis Analyticae Praxis ad Aequationes Algebraicas Resolvendas
- ↑ Fite 1921, p. 19
- ↑ Selby 1970, p. 101
- ↑ Dickson 1922, p. 27
- ↑ Stover, Christopher AC Method - Mathworld Arquivado 2014-11-12 en Wayback Machine.
- ↑ Nun anel de característica 2, tense que 2=0 que produce que na fórmula haxa unha división entre 0.
- ↑ Burnside & Panton 1960, p. 38
Véxase tamén[editar | editar a fonte]
Bibliografía[editar | editar a fonte]
- Burnside, William Snow; Panton, Arthur William (1960) [1912]. Dover, ed. The Theory of Equations with an introduction to the theory of binary algebraic forms (Volume one).
- Dickson, Leonard Eugene (1922). John Wiley & Sons, ed. First Course in the Theory of Equations. New York.
- Fite, William Benjamin (1921). D. C. Heath & Co., ed. College Algebra (Revised). Boston.
- Klein, Felix (1925). Dover, ed. Elementary Mathematics from an Advanced Standpoint; Arithmetic, Algebra, Analysis.
- Selby, Samuel M. The Chemical Rubber Co., ed. CRC Standard Mathematical Tables (18 ed.).
Ligazóns externas[editar | editar a fonte]
- Wolfram Alpha [1] é capaz de realizar factorizacións.































































































































![{\displaystyle \mathbb {Z} [{\sqrt {-5}}],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/643ef2c1e3b8b8e684a0ddf73d649cb0202cc0c1)
